9.3. Алгоритм

9.3. Алгоритм

«Принцип обогащения» применительно к решению задачи о коммивояжере (ЗОК) заключается в следующем: с помощью некоторого условия проверить все ветви графа на наличие полезных свойств (в данном случае это «способность» участвовать в оптимальном гамильтоновом цикле) и для дальнейшего решения задачи оставить только эти «полезные» ветви. В случае, когда используемое условие достаточно сильно, после этой проверки останутся только ветви оптимального гамильтонова цикла. В другом случае из рассмотрения будет исключена часть ветвей графа, что дает возможность сократить время поиска решения с применением какого-либо алгоритма.

Таким образом, весь процесс решения задачи делится на 2 стадии: первая – «обогащение» исходного числового массива, вторая – применение алгоритма поиска на «обогащенном» массиве.

Реализация первой стадии при решении ЗОК возможна с применением полученного в разделе 9.2 условия оптимальности гамильтонова цикла в графе G с п вершинами.

Условие оптимальности можно использовать для «обогащения» исходного множества ветвей графа: после проверки всех ветвей графа на условие оптимальности число ветвей, которое целесообразно использовать при дальнейшем решении ЗОК, сократится. Ввиду очевидной простоты описание алгоритма не приводится.

Опыт применения этого условия для графов с п = 11–67 показал, что после однократного применения такой операции ко всем ветвям графа число ветвей в обогащенном массиве сокращается, как правило, до 15% от первоначального.

Для поиска оптимального гамильтонова цикла на обогащенном массиве использовался следующий метод. Известно, что существующие алгоритмы решения ЗОК не ставят целью обеспечение или проверку а-оптимальности получаемого гамильтонова цикла.

Предлагаемый алгоритм основан на последовательном обеспечении а-оптимальности решения ЗОК на обогащенном массиве исходных данных и состоит в выполнении следующих операций.

Алгоритм «а-оптимум».

0. Задаем произвольно исходный гамильтонов цикл i₁, …, i_k, …, i_n, i₁ с весом ? (i₁, …, i_n, i).

1. 3адаем значение а; а=4,5, …,п, п+1.

2. Задаем значение k; k=1,2,…,п,1,2, …,п,2,… .

3. Для вершины i_k сравниваем все последовательности на а вершинах, i_k, …, i_k+a-1, получаемые перестановками а-2 промежуточных вершин между i_k и i_к+а-1 по их весам р(i_к,…, i_k+a-1), и выбираем последовательность с наименьшим весом. При этом последовательности, содержащие ветви с весом, равным бесконечности (между этой парой вершин нет соединения), отбрасываем сразу, не вычисляя веса.

Если веса всех последовательностей в операции 3 равны, либо вес ? (i_k, i_k+1, …, i_k+a-2, i_k+a-1) является минимальным, оставляем в гамильтоновом цикле последовательность i_k, i_k+1, i_k+a-1, имевшую место в начале операции 3 для данного k. Этот факт фиксируем и переходим к операции 4.

Если таких последовательностей несколько, то из них выбираем первую по счету, вводим ее в гамильтонов цикл вместо соответствующей прежней и переходим к операции 2, где задается очередное значение k.

4. Фиксируем значение k. Проверяем все зафиксированные ранее значения k. Если ранее зафиксированы не все значения k, то переходим к операции 2, где задается очередное значение k. Если ранее зафиксированы все значения k=1,2,…, п, то полученный гамильтонов цикл а-оптимален. Переходим к операции 5.

5. Проверка одинаковости решений при а-2, а-1, а.

Примечание. Оптимальный ((п+1)-оптимальный) гамильтонов цикл а-оптимален для всех значений а. Но такая проверка для больших значений а требует неприемлемых затрат времени. Поэтому для конкретных задач можно ограничиться обеспечением условия совпадения а-оптимальных гамильтоновых циклов для нескольких последовательных значений а, например трех (т.е., когда удлинение проверяемых последовательностей на одну, две ветви не дает улучшения результата).

Если хотя бы одно решение отличается от других, переходим к операции 1, где задается новое значение а. Если все три решения равны, считаем результат – полученный а-оптимальный гамильтонов цикл – удовлетворительным решением ЗОК. Последовательность выполнения операций алгоритма показана на графе (рис.9.1).

Работа алгоритма «а-оптимум» анализировалась для различных п.

При решении задач метод «обогащения» исходного множества ветвей и алгоритм «а-оптимум» использовались совместно. Во всех приведенных случаях такой совместный счет эффективнее алгоритма «а-оптимум» на необогащенном множестве ветвей графа.

С соответствующими изменениями предложенные методы «обогащения» и «а-оптимизации» могут использоваться и для задач поиска а-оптимальных простых путей и циклов (или их совокупностей), покрывающих т ? п вершин графа.

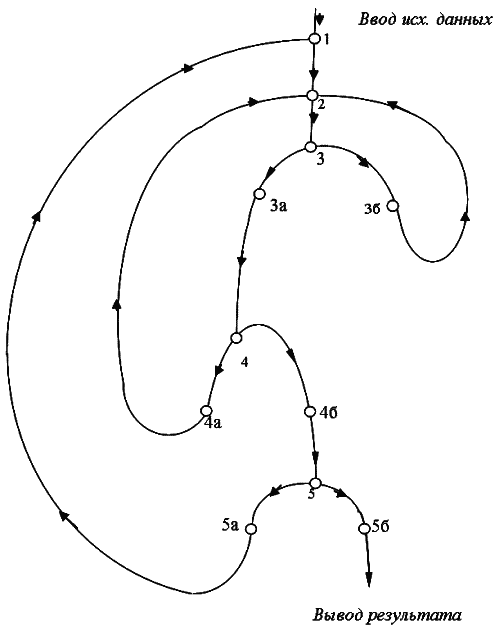
Рис.9.1. Схема алгоритма «а-оптимум»

Данный текст является ознакомительным фрагментом.