Примечания
Примечания
1. Тем, кого интересуют подробности развития дифференциального исчисления, понравится книга Карла Бойера «История дифференциального исчисления» (Carl Boyer. The History of Calculus).
2. Будем обозначать расстояние буквой s. Возьмем две точкиX и х, лежащие
на одной прямой линии, и обозначим расстояние между ними как s = X – х, или в графической форме X <–s–> x.
Будем обозначать это расстояние как «X– x» или «дельта s». Дельта – это буква А греческого алфавита, которая в математике используется для обозначения небольшого изменения чего-либо.
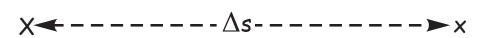
Рис. 11.4. Небольшое расстояние между двумя точками на прямой
Допустим, наши часы показывают 5.02 когда вы начинаете свой путь в точке X, и 5.03 когда вы доходите до точки х. В общем случае, будем обозначать разницу во времени между одним и другим измерениями как ?t. Как мы помним, А – это сокращенное обозначение «небольшого изменения». Таким образом, для прохождения расстояния ?s нам требуется время ?t.
Теперь давайте подумаем о скорости. Если скорость показывает, как быстро вы идете в каждой точке пути, то теперь мы можем измерять скорость, говоря, что скорость равна количеству расстояния, вроде ?s, которое вы проходите за определенное количество времени – вроде ?t.
Теперь нам известно, что означает скорость движения между двумя точками, – это время, которое вам нужно, чтобы дойти от одной из них до другой. Если точки находятся далеко друг от друга, мы можем находить среднюю скорость. Допустим, вы подсчитываете, что в некоторой точке P между a и с вы, в среднем, проходили 2 + 4 фута за 2 секунды (см. ниже), что означает среднюю скорость 3 фута в секунду. Но если мы проводим более точные измерения, то знаем, что 3 фута в секунду – это средняя, а не ваша фактическая скорость в точке P!

Рис. 11.5. Время и расстояние для короткого пути
Но нам мало знать средние значения. Мы хотим достичь действительной определенности и знать, что означает скорость в одной данной точке.
Как мы можем говорить, что в одной точке вы идете со скоростью 3 фута в секунду или 3 мили в час? Эту проблему пришлось решать Ньютону.
Он полагал, что вашу скорость в данной точке P между X и x можно приближенно вычислять, исходя из скорости между двумя точками вблизи P. Небольшое расстояние – скажем, 2 дюйма – в окрестности точки P выглядело бы следующим образом.

Рис. 11.6. Время и расстояние для более короткого пути
Допустим, наш секундомер показывает, что для прохождения этих двух дюймов, которые мы называем ?s, требуется очень небольшое время ?t, например одна десятая доля секунды. Тогда скорость в точке P равна отношению ?s /?t, то есть двум дюймам, деленным на одну десятую секунды. Другим словами,
скорость = ?s /?t = 2 дюйма в каждые 0,1 сек, или сокращенно:
? = ?s /?t = 20 дюймов в секунду.
Если подсчитать, то 2 дюйма за одну десятую секунды равносильны 1,136 мили в час, что довольно медленно для человека. Скорость 1,136 мили в час означает лишь то, что если бы я продолжал идти 1,136 мили точно в том же темпе, в каком я шел те 2 дюйма, то прошел бы эти 1,136 за один час.
(Вот как это можно подсчитать: Умножая верх и низ отношения на 10, мы получаем 20 дюймов в секунду. Умножая на 60, получаем 1200 дюймов в минуту или 72000 дюймов в час, то есть 6000 футов в час или 1,136 американской мили в час, поскольку американская миля равна 5320 футов!)
3. Иными словами, ? – это флюксия, которая определяется как
Lim ?s = ?s /?t = v
?t ? ? 0
(где термин «lim» означает предел ?s, когда ?t стремится к нулю)
Ньютон называл
v = Lim ?s = ?s /?t
«флюксией». Позднее математики изменили название «флюксия» на «производная»; в нашем примере это производная s относительно t. Иногда ds/ dt пишут просто как букву s с точкой над ней. Это изменение названия весьма прискорбно, так как изучающие дифференциальное исчисление больше не слышат термин «флюксия» и забывают, что ds/dt – это, в действительности, флюксия – другой мир, который встречается с этим миром в пределе, когда детали становятся очень мелкими.
ds/dt составляет основу дифференциального и интегрального исчисления, которые играют ключевую роль в физике всего, что движется.
4. Как описано в примечании 3, флюксия представляет собой отношение двух дифференциалов, например пространства и времени, то есть ds/dt.
5. Помните старую сказку «Ханзель и Гретель», пересказанную Братьями Гримм? Маленький мальчик Ханзель и девочка Гретель сумели ночью найти путь домой из домика ужасной колдуньи по крупинкам, которые они оставляли по пути из дома в лес, где жила колдунья. Ночью, убегая от ведьмы, они следовали по пути крупинок.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ (с.343) Penck A. Das Hauptproblem der physischer Antropogeographie // “Geopolitik”, 1925. S. 330-348. Инцухт (нем. Inzucht) – близкородственное скрещивание организмов. [с.349] Форейтор (нем.) – верховой, сидящий на одной из передних лошадей, запряженных цугом. [с.349] В 1280 г. Китай целиком оказался под властью
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ В христианской мифологии мотив пахоты (и сева) приобретает смысл духовного труда во имя спасения. Как убедится читатель, ознакомившись с текстом данного сочинения, под безобидными метафорами “вспашка”, “сев”, “всходы” и т.п. автор по существу понимает
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ Из всех произведений К. Хаусхофера, включенных в данный том, работа “Континентальный блок”, несомненно, является наиболее спорной. Здесь ученый-эрудит вступает в противоречие с ангажированным публицистом, взявшим на себя явно несостоятельную задачу, а
Примечания
Примечания I. Кто убил старика Карамазова?1 9, 105.2 9,589.3 Здесь и везде ниже разрядка в цитатах дана автором настоящей работы. — Ред.4 9,593.5 10,114.6 10,117–118.7 10,118.8 9, 606.9 10, 144.10 10, 144–145.11 10,291.12 10, 145.13 10, 147.14 10, 150.15 10, 170.16 10, 155.II. Убийца-дублер1 10, 138.2 10,231.3 10, 126.4 10, 145.5 10,155.6 10,168.7 Есмь «и ничто
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ К новому изданию 1963 г. Работа «Фридрих Ницше — борец против своего времени» вышла в свет в 1895 г. Второе издание Рудольф Штейнер собирался выпустить в 1921 г., снабдив его предисловием. Книга была полностью готова и набрана. По причине перегруженности работой
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ Сокращенный перевод примечаний, составленных издателями немецкого текста (Rudolf Steiner. Metamorphosen des Seelenlebens. Pfade der Seelenerlebnisse. Erster Teil. Rudolf Steiner Verlag, Dornach/Schweiz, 1984).Текст берлинских лекций основан на стенографической записи Вальтера Фегелана; он же и расшифровал ее.
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ Настоящий том произведений А. Ф. Лосева целиком составляют работы, ранее не публиковавшиеся — если не считать небольших отрывков из «Диалектических основ математики>ч(Начала. 1993. № 2; 1994. № 2—4). Все работы обнаружены в архиве автора. Содержание тома можно
Примечания
Примечания Введение 1 Гегель. История философии. Т. 1.2 Кант. Пролегомоны ко всякой будущей метафизике.3 Гегель. История философии. Т. 1.4 Там же. Т. 3.5 Предисловие к первому изданию «Критики чистого разума».6 Гегель. История философии. Т.