Примечания
Примечания
1. Из книги «Французские легенды, истории и сказки» Барбары Леонии Пикар с иллюстрациями Джоан Кидделл-Монро. История Мелузины широко распространена. Варианты этой истории существуют в Северной Африке, Южной Америке, Европе и Китае.
2. Чтобы понять смысл неопределенности в квантовой физике, давайте рассмотрим эксперимент, предложенный Ричардом Фейнманом в «Фейнма-новских лекциях по физике» (т. II, гл. 1, С. 1). Цель эксперимента – исходить из противоположного, ставить под сомнение выводы Гейзенберга и пытаться доказать, что его принцип неопределенности ошибочен. Иными словами, мы хотим попытаться точно определить положение и импульс электрона.
Пусть значок * на рис. 16.2 соответствует электрону. Допустим, что мы узнаем о присутствии электрона по щелчку счетчика электронов на экране. Счетчики изображены квадратными скобками. Изображенная слева электронная пушка испускает электроны. Электроны проходят через перегородку с двумя щелями. Эта перегородка слегка отличается о той, которую мы рассматривали в главе 14. Кружочки над и под щелями в перегородке соответствуют бегункам – колесикам, которые позволяют перегородке колебаться вверх и вниз, если ее толкают электроны, проходящие через щели.
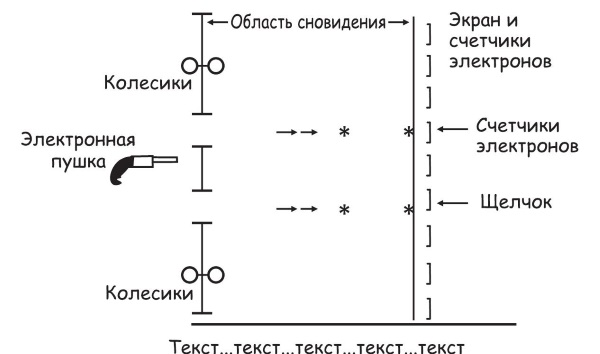
Рис. 16.2. Новый эксперимент с подвижной подвеской перегородки, с помощью которого не удалось опровергнуть принцип неопределенности
Позволит ли этот эксперимент с уверенностью определять положение и импульс электрона? Давайте посмотрим. Если электрон попадает в верхнюю щель, он толкает перегородку немного вверх; если электрон попадает в нижнюю щель, он толкает перегородку немного вниз. В каждом случае мы можем измерять толчок (импульс) по тому, насколько перегородка сдвинулась или качнулась вверх или вниз.
Если бы мы знали вес перегородки и ее скорость после толчка, то могли бы вычислить импульс электрона в данном положении и обойти принцип неопределенности. (Если M – это масса перегородки, V – ее скорость, m – масса электрона, а v – его неизвестная скорость, то в силу закона сохранения импульса MV = mv мы узнаем импульс частицы, измеряя скорость перегородки.)
Мы можем определить импульс электрона по тому, как он толкает перегородку. И мы знаем его положение, поскольку, если электрон попадает в верхнюю щель, перегородка движется вверх, а если он попадает в нижнюю щель, перегородка движется вниз. Итак, у нас получилось. Мы перехитрили принцип неопределенности.
Верно? Нет, не верно. Мы упустили небольшую проблему. Если перегородка качается, то мы больше не знаем ее точное положение, и когда через нее проходит следующий электрон, положение щели изменится. Возможно, мы измерили положение и импульс для одного электрона, но эксперимент изменился, поскольку изменилась обстановка следующего измерения. Незначительные движения перегородки меняют распределение на экране. Оказывается, что движения перегородки нейтрализуют волновой эффект.
Таким образом, если мы с большой точностью прослеживаем положение электрона, то нарушаем эксперимент и больше не получаем волновой эффект, независимо от того, насколько хорошо мы готовим эту систему. Ученые пробовали много других экспериментов, пытаясь перехитрить принцип неопределенности, но потерпели неудачу. Можно иметь лучшие колесики, более легкую перегородку, которая лучше двигается, но ее колебания сводят волны на нет.
Это подтверждают экспериментальные результаты, которые показывают, что частицы больше не ведут себя как волны, после того как проходят через две щели в перегородке, снабженной бегунками. Определение импульса и положения электрона в пути заставляет его вести себя применительно к наблюдениям на экране подобно обычной частице. Мораль этой истории в том, что, когда мы смотрим слишком пристально, электрон утрачивает свою волноподобную природу и превращается в частицу.
3. Символ h соответствует общей, особой, природной постоянной, которая, насколько нам известно, никогда не меняется. Постоянная h приблизительно равна 6,63 х10-34 джоулей-секунд. Таким образом, для данного импульса мы можем быть уверены только в том, что частица попала в область ?х!
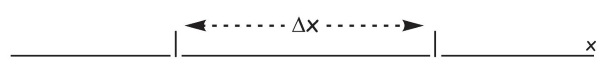
Рис. 16.3. Неопределенность в отношении положения
4. Поскольку ?е х ?t > h, если нам нужно 3 секунды, то мы находим, что ?е х 3 > h или ?e > h/3.
5. В силу знаменитого уравнения E = mc2, немного дополнительной энергии в течение доли секунды позволяло бы нам иметь немного дополнительной массы.
6. Мы могли бы сказать вместе с Юнгом, что сознательная и бессознательные сферы взаимодополнительны. Чтобы понимать сновидение, вы должны знать сознательную ситуацию сновидца. Юнг говорил о дополнительности в своей работе «Структура и динамика психики» (Собрание сочинений, том VIII).
7. Мы обнаруживаем неопределенность даже в математических описаниях волны. В главе 15 мы видели, что представлению о частице в квантовой механики может соответствовать нечто, именуемое волновым пакетом. Математическая идея частицы – это микроскопический волновой пакет размером в одну миллионную или миллиардную сантиметра. Частица представляет собой не четко определенную вещь, а пучок волн, которые собираются в блок. Интересно, что даже при таком «блочном» описании невозможно определить импульс частицы, поскольку нам бы потребовалось идентифицировать блок по одной конкретной волновой частоте. А для волнового пакета нет единичной волновой частоты.
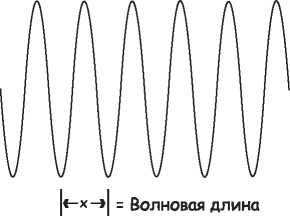
Рис. 16.4. Волновая длина волны
Например, единичная волна имеет данную волновую длину х. Но волновой пакет, показанный на рис. 16.5, не имеет никакой единственной волновой длины.
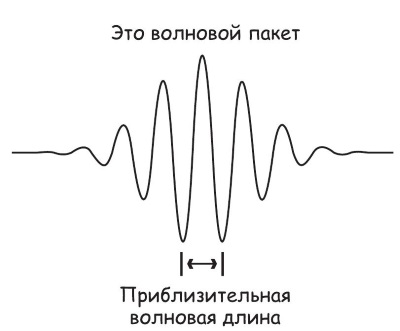
Рис. 16.5. Неопределенность в частоте волновых пакетов
Волновые пакеты интересны потому, что они, как группы волн, приближенно описывают природу частиц, движущихся в пространстве и времени.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ (с.343) Penck A. Das Hauptproblem der physischer Antropogeographie // “Geopolitik”, 1925. S. 330-348. Инцухт (нем. Inzucht) – близкородственное скрещивание организмов. [с.349] Форейтор (нем.) – верховой, сидящий на одной из передних лошадей, запряженных цугом. [с.349] В 1280 г. Китай целиком оказался под властью
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ В христианской мифологии мотив пахоты (и сева) приобретает смысл духовного труда во имя спасения. Как убедится читатель, ознакомившись с текстом данного сочинения, под безобидными метафорами “вспашка”, “сев”, “всходы” и т.п. автор по существу понимает
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ Из всех произведений К. Хаусхофера, включенных в данный том, работа “Континентальный блок”, несомненно, является наиболее спорной. Здесь ученый-эрудит вступает в противоречие с ангажированным публицистом, взявшим на себя явно несостоятельную задачу, а
Примечания
Примечания I. Кто убил старика Карамазова?1 9, 105.2 9,589.3 Здесь и везде ниже разрядка в цитатах дана автором настоящей работы. — Ред.4 9,593.5 10,114.6 10,117–118.7 10,118.8 9, 606.9 10, 144.10 10, 144–145.11 10,291.12 10, 145.13 10, 147.14 10, 150.15 10, 170.16 10, 155.II. Убийца-дублер1 10, 138.2 10,231.3 10, 126.4 10, 145.5 10,155.6 10,168.7 Есмь «и ничто
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ К новому изданию 1963 г. Работа «Фридрих Ницше — борец против своего времени» вышла в свет в 1895 г. Второе издание Рудольф Штейнер собирался выпустить в 1921 г., снабдив его предисловием. Книга была полностью готова и набрана. По причине перегруженности работой
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ Сокращенный перевод примечаний, составленных издателями немецкого текста (Rudolf Steiner. Metamorphosen des Seelenlebens. Pfade der Seelenerlebnisse. Erster Teil. Rudolf Steiner Verlag, Dornach/Schweiz, 1984).Текст берлинских лекций основан на стенографической записи Вальтера Фегелана; он же и расшифровал ее.
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ Настоящий том произведений А. Ф. Лосева целиком составляют работы, ранее не публиковавшиеся — если не считать небольших отрывков из «Диалектических основ математики>ч(Начала. 1993. № 2; 1994. № 2—4). Все работы обнаружены в архиве автора. Содержание тома можно
Примечания
Примечания Введение 1 Гегель. История философии. Т. 1.2 Кант. Пролегомоны ко всякой будущей метафизике.3 Гегель. История философии. Т. 1.4 Там же. Т. 3.5 Предисловие к первому изданию «Критики чистого разума».6 Гегель. История философии. Т.