Примечания

Примечания

1. Роберт Оссерман в своей чудесной и занимательной книге «Поэзия Вселенной» (глава 1) подробно рассказывает о том, как измерять размер Земли и ее расстояние от Солнца.

2. Об этом можно прочитать в книге Роберта Оссермана и Уты Мерцбах «История математики».

3. Гёдель показал, что в рамках жесткой логической системы, подобной системе арифметики, можно формулировать утверждения, однако невозможно демонстрировать их справедливость в рамках логики или аксиом этой системы. В этих логических системах всегда будут существовать определенные краткие утверждения, которые невозможно ни доказать, ни опровергнуть. Другими словами, невозможно узнать, приведут ли аксиомы арифметики к противоречиям. Это, по-видимому, разрушает всякую надежду на достижение математической определенности путем использования наиболее очевидных методов. Судя по всему, пока физика придерживается только математики в ее существующем состоянии, у нее никогда не будет набора аксиом, из которых можно выводить все феномены природного мира. Однако ученые все еще надеются найти способ удостовериться в существовании возможности определения того, является ли каждое из их математических утверждений истинным, ложным, или неразрешимым. До сих пор никому не удалось найти такой способ.

4. См., например, совершенно замечательную книгу Роберта Лоулора «Священная геометрия» (Robert Lawlor, Sacred Geometry), в которой он великолепно соединяет геометрию и мифологию.

5. Подобные пробуждения описаны в моей книге «Кома, ключ к пробуждению».

6. См. книгу Люси Лейми «Древнеегипетские мистерии: древнее знание в новом свете» (Lucie Lamy, Egyptian Mysteries: New Light on Ancient Knowledge) стр.8.

7. Там же, стр. 8, 14.

8. Лоулор, цит. ист. стр. 102 и далее.

9. Лоулор, цит. ист. стр. 11.

10. Лоулор, цит. ист. стр. 13.

11. Эта цитата взята из книги Филиппа Франка «Эйнштейн, его жизнь и время (Philipp Frank, Einstein, His Life and Times, 1947).

12. Пространственно-временные интервалы можно было бы записывать как

s² = х₁² + x₂² + x₃² + x₄² или s² = x² + y² + z² + (-ict)².

13. Если для простоты забыть об измерениях у и z, то пространственновременной интервал становится легче понять. Он приобретает вид

s² = x₁² + x₄² = x² – (ct)².

14. Результат мнимых чисел в пространстве-времени связывает измерение времени со знаком минус. Подставляя в формулу s² = (a² – b²) реальные величины a и b – скажем, a = 1 и b = 2 – мы получаем:

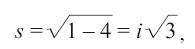
поскольку корень квадратный из отрицательного числа дает мнимое число. Если a больше b – например, a = 3 и b = 1, – то мы получаем действительное число, в данном случае корень квадратный из двух, равный примерно 1,4.

15. Математическая разрывность подобна очень глубокой яме на дороге. В математике что-либо становится разрывным, когда вы пытаетесь делить какое-либо число на ноль. Деление двух чисел – простая операция: например, 2/1 = 2. Сходным образом, 2/0,5 = 4. Но 2/0? Это бесконечность. В общей теории относительности числа типа 2/0 присутствуют как «разрывности», создающие у астрономов впечатление, что уравнения теории относительности указывают на существование дыр в пространстве-времени – черных дыр.