§ 3. Эквивалентные суждения

§ 3. Эквивалентные суждения

Осознание того, что одно и то же может быть сказано различными способами, оказалось весьма ценным для отыскания истины. Пустые споры столь часты не только потому, что каждый предпочитает собственную формулировку отстаиваемых верований, но еще и потому, что из-за подобного предпочтения мало кто готов проанализировать чужие высказывания, якобы выражающие противоположную точку зрения, с тем чтобы понять, являются ли видимые отличия в этих высказываниях существенными или только вербальными. Как бы то ни было, в изучении того, какие суждения являются эквивалентными, заключена существенная часть рационального исследования.

В традиционной логике рассматривались несколько форм эквивалентных суждений. При их изучении читатель может пользоваться схематическими изображениями категорических суждений или алгебраической записью, выражающей их суть.

Обращение (конверсия)

Рассмотрим, что утверждается в суждении «ни одна сельскохозяйственная страна не является толерантной в вопросах религии». Очевидно, что это суждение содержит ту же информацию, что и суждение «ни одна страна, являющаяся толерантной в вопросах религии, не является сельскохозяйственной», поскольку если сельскохозяйственные страны исключены из стран, считающихся толерантными, то толерантные страны тоже должны быть исключены из стран, считающихся сельскохозяйственными. Данные два суждения – эквивалентны: если одно истинно или ложно, то другое тоже истинно или ложно соответственно. У них на месте субъекта и предиката стоят одни и те же термины с той лишь разницей, что субъект первого суждения является предикатом второго, а предикат первого – субъектом второго. Второе суждение называется конверсным суждением относительно первого. Процесс, с помощью которого мы переходим от одного суждения к другому, обладающему тем же истинностным значением и в котором субъект первого является предикатом, а предикат – субъектом, называется обращением (конверсией). Суждение типа Е, следовательно, может быть преобразовано с помощью конверсии.

Можно ли преобразовать все остальные типы категорических суждений? Можем ли мы из суждения «все лысые люди чувствительны» обоснованно вывести суждение «все чувствительные люди – лысые»? Разумеется, не можем. Читатель сможет убедиться в этом более наглядно, если обратит внимание на то, что в первом суждении термин «чувствительны» является нераспределенным, тогда как после обращения этот же термин является распределенным. Это недопустимо, поскольку является равносильным утверждению чего-либо относительно всего класса на основании утверждения, относящегося лишь к неопределенной части этого класса. Итак, мы можем сформулировать общий принцип: в умозаключениях с категорическими суждениями термины, нераспределенные хотя бы в одной из посылок, не могут быть распределенными в заключении. Следовательно, на основании суждения «все лысые люди чувствительны» мы можем вывести только суждение «некоторые чувствительные люди – лысые». Таким образом, суждение типа А может быть обращено только посредством ограничения или per accidens [26] , т. е. при изменении его количества. Однако, как мы видели выше, умозаключение per accidens является обоснованным только при допущении того, что класс, обозначаемый субъектом, содержит членов, в данном случае – лысых людей.

Конверсным суждением для суждения типа I «некоторые республиканцы – консерваторы» является суждение «некоторые консерваторы – республиканцы». Следовательно, обращение суждения типа А одновременно является обращением подчиненного ему суждения.

Какое суждение будет конверсным суждением для суждения «некоторые итальянцы не брюнеты»? Быть может, читателю хочется сказать, что им является суждение «некоторые брюнеты не итальянцы»? Однако очевидно, что такой вывод будет неверным. Из суждения «некоторые смертные не люди» не следует суждения «некоторые люди не смертны». Технически говоря, подобное умозаключение нарушает принцип о распределенности терминов: суждение типа О не имеет конверсивного суждения. Однако, как мы убедимся ниже, из него мы сможем заключить, что «некоторые люди, не являющиеся брюнетами, итальянцы».

Превращение (обверсия)

Эквивалентные суждения можно получить и иным путем. Если нам дано суждение «приветствуются все работники», то что мы можем заключить об отношении между работниками и теми, кто приветствуется? Очевидно, что суждение «ни один работник не является не приветствующимся» будет обоснованным заключением. Эти два суждения являются эквивалентными: в первом говорится, что нет таких, кто был бы работником и не приветствовался бы; во втором суждении утверждается то же самое. Такое умозаключение называется «превращением», а каждое из этих двух суждений является обверсивным относительно другого. Субъекты в этих суждениях одни и те же, но предикативный термин одного из них является отрицанием или противоречием другого; также данные суждения являются различными по качеству. Необходимо внимательно следить за тем, чтобы предикат обверсивного суждения в заключении был противоречием предиката в посылке. Так, обверсивным суждением относительно «все листья – желтые» не будет суждение «ни один лист не является синим», т. к. «зеленый» и «синий» не противоречащие термины, а только лишь противоположные. Два термина являются противоречащими в предметной области, если их объемы не только полностью исчерпывают эту область, но и исключают друг друга; объемы противоположных терминов лишь исключают друг друга. Обверсивным суждением для суждения «все листья – зеленые» будет суждение «ни один лист не является незеленым» или, проще говоря, «нет листьев, кроме зеленых».

Превращенными могут быть все четыре типа категорических суждений без каких-либо ограничений. Читателю следует самостоятельно удостовериться в том, что обверсивным суждением для «ни один лапландец не является образованным» будет суждение «все лапландцы – необразованные», для суждения «некоторые президенты колледжей умны» – «некоторые президенты колледжей не являются неумными», для суждения «некоторые газы не являются ядовитыми» – «некоторые газы являются неядовитыми».

Обращение и превращение – две формы умозаключения, в котором происходит переход от одного суждения к эквивалентному ему суждению. Остальные типы, изучаемые в традиционной логике, можно определить как результаты последовательного применения этих двух типов.

Противопоставление предикату (контрапозиция)

Возьмем суждение «все разумные прошения рассматриваются». Что на его основании можно заключить об отношении нерассматриваемых вещей, с одной стороны, к разумным прошениям, а с другой стороны, к неразумным прошениям? Читатель может признать, что допустимым заключением будет суждение «ни одна нерассматриваемая вещь не является разумным прошением», а также суждение «все нерассматриваемые вещи суть неразумные прошения». Однако в случае, если читатель не усматривает, что данные заключения являются необходимыми, ему следует осуществить следующую серию превращений и обращений. Мы рассмотрим все четыре категорических суждения вместе.

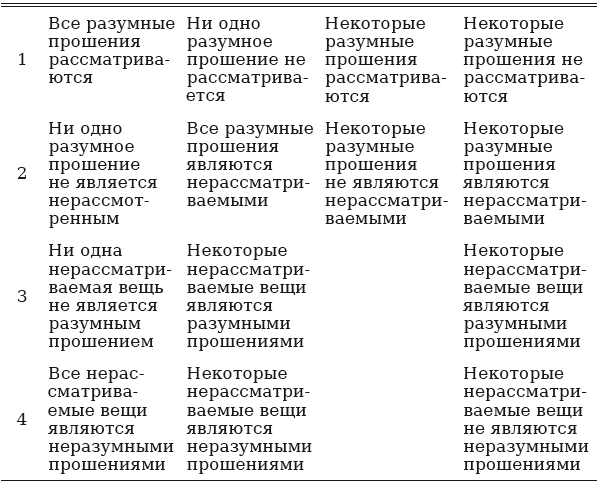
Первый ряд содержит четыре категорических суждения. Второй ряд содержит соответствующие обверсивные суждения. Третий ряд содержит конверсивные суждения относительно суждений из второго ряда. А четвертый ряд содержит обверсивные суждения относительно суждений из третьего ряда.

Суждения в третьем ряду называются частично противопоставленными (контрапозитивными) предикату суждений в первом ряду. Частично противопоставленное предикату суждение относительно какого-либо суждения – это суждение, в котором субъект является противоречием предиката исходного суждения, тогда как предикат является субъектом исходного суждения. Частично противопоставленное предикату суждение также отличается от исходного суждения по качеству. Суждения типа I не имеют частично противопоставленных предикату суждений, а суждения типа Е обретают частично противопоставленное предикату суждение только посредством ограничения. Суждения, частично противопоставленные предикату суждений типа А и О, эквивалентны исходным суждениям.

Суждения в четвертом ряду являются суждениями, полностью противопоставленными предикату соответствующих суждений из первого ряда. Суждение, полностью противопоставленное предикату некоторого другого суждения, – это суждение, в котором субъект является противоречием исходного предиката, а предикат – противоречием исходного субъекта. Полностью противопоставленное предикату суждение имеет то же качество, что и исходное суждение. Как и в случае с частично противопоставленным предикату суждением, суждения типа I не обладают суждениями, полностью противопоставленными предикату, а суждения типа Е обретают их только посредством ограничения.

Превращенное конверсное суждение

Проводя серии превращений и обращений именно в таком порядке, мы получали эквивалентные суждения для каждого из четырех типов категорических суждений. Однако если мы сначала преобразуем суждения с помощью обращения, а затем с помощью превращения, то получим иной набор эквивалентных суждений. Результаты такой операции приводятся в таблице ниже:

Следует отметить, что суждения типа Е и I обладают превращенными конверсными суждениями без посредства ограничения, суждения типа А обретают превращенное конверсное суждение посредством ограничения, тогда как суждения типа О вообще таковыми не обладают.

Инверсия

Дано суждение «все физики являются математиками». Что можно заключить об отношении не-физиков к математикам или к не-математикам? Рассмотрим, к каким заключениям можно обоснованно прийти с помощью обращений и превращений.

Мы можем начать с обращения данного суждения, затем осуществить превращение и т. д. до тех пор, пока не получим требующееся суждение; или же мы можем начать с превращения и продолжить обращением и т. д. Попробуем развить эти два метода в параллельных столбцах. Первый метод – в левом столбце, второй – в правом:

Следовательно, если мы сначала обратим суждение типа А, мы вскоре вынуждены будем остановиться, поскольку суждение типа О не может быть обращено. Если же мы сначала превратим суждение А, то получим два суждения, которые будут удовлетворительными. «Некоторые не-физики не являются математиками» называется частично инверсивным суждением относительно исходного суждения. Его субъект является противоречием исходного субъекта, а его предикат совпадает с исходным предикатом. «Некоторые не-физики являются не-математиками» называется полностью инверсивным суждением. В нем как субъект, так и предикат противоречат исходным субъекту и предикату соответственно.

Все ли формы категорического суждения обладают инверсивным суждением? Если читатель использует указанный метод, то из суждения «ни один профессор не является недобрым» он сможет вывести суждение «некоторые не-профессора являются недобрыми» (частично инверсивное суждение) и «некоторые не-профессора не являются добрыми» (полностью инверсивное суждение). Однако из суждения типа I и О инверсивные суждения получить нельзя. Следовательно, только общие суждения обладают инверсивными суждениями, и в каждом случае инверсия осуществляется посредством ограничения.

Операция инверсии иногда может приводить к кажущимся абсурдными результатам, как, например, при получении из суждения «все честные люди смертны» инверсивного суждения «некоторые бесчестные люди бессмертны». На каком этапе вкралась ошибка? Ответ: при небрежном использовании отрицаний. Настоящим инверсивным суждением относительно исходного будет суждение «некоторые из тех, кто не является честным человеком, являются не-смертными», которое вовсе не абсурдно. Класс сущностей, не являющихся честными людьми, шире класса бесчестных людей и включает в себя треугольники и т. п., которые, разумеется, являются не-смертными.

«Одну минутку!» – может возразить читатель. «Частично инверсивным суждением для суждения «все физики являются математиками» является суждение «некоторые не-физики не являются математиками». В первом суждении предикат нераспределен, тогда как во втором – распределен. Как же можно утверждать, что второе суждение является обоснованным следствием первого? Нет ли здесь нарушения принципа о распределенности терминов?»

Если читатель усвоил наше обсуждение вопроса об экзистенциальной нагруженности суждений, то он без труда сможет ответить на свой вопрос. В общем суждении, скажет он, не утверждается ничего о существовании или несуществовании чего-либо; частные суждения, с другой стороны, обладают экзистенциальной нагруженностью. Следовательно, частное суждение может обоснованно выводиться из общего суждения или их сочетания, только если среди посылок есть суждение, утверждающее, что классы, обозначаемые терминами общих суждений, содержат, по крайней мере, один член. В частности, обращение суждения типа А является обоснованным, только если предикат обозначает такой непустой класс.

Источник сложностей с инверсией теперь прояснен. Чтобы получить инверсивное суждение из суждения «все физики – математики», нам нужно обратить суждение «все не-математики являются не-физиками». Это возможно, только если мы добавим третью посылку: «Некоторые люди являются не-физиками». Если такая посылка имеется, то частично инверсивное суждение не нарушает принципа распределенности терминов.

Если бы общие суждения обладали экзистенциальной нагруженностью, то тогда не только термины подобных суждений обозначали бы непустые классы, но их обозначали бы и противоречивые термины. Так, если бы суждение «все люди смертны» требовало наличия людей и смертных существ, то, поскольку из него мы можем обоснованно вывести суждение «все бессмертные являются не-людьми», нам бы пришлось утверждать и то, что существуют сущности, являющиеся бессмертными, и сущности, являющиеся не-людьми. Следующий пример призван продемонстрировать, что общие суждения не имеют экзистенциальной нагруженности даже в обычной разговорной речи. Студенты-математики знакомы с древнегреческой проблемой, заключающейся в том, что построить с помощью линейки и циркуля квадрат, площадь которого будет равна площади окружности, невозможно. Следовательно, мы можем с уверенностью утверждать суждение «ни один математик не построил круг, одинаковый по площади с квадратом». Частично инверсивным суждением относительно данного будет суждение «некоторые не-математики являются построившими круг, одинаковый по площади с квадратом». Однако мы, несомненно, не намеревались утверждать что-либо, приводящее к заключению о том, что существуют люди, которые на самом деле могут построить такой круг, поскольку существует доказательство, согласно которому подобное не может быть сделано. Следовательно, в исходном суждении не предполагалось утверждения существования таких людей.

Умозаключение посредством обратного отношения

Из суждения «Чикаго расположен к западу от Нью-Йорка» можно обоснованно вывести суждение «Нью-Йорк расположен к востоку от Чикаго», из суждения «Сократ был учителем Платона» – суждение «Платон был учеником Сократа», из «семь больше пяти» – «пять меньше семи». Каждая из приведенных пар суждений представляет два эквивалентных суждения. Такие умозаключения имеют следующую форму: если а находится к Ь в определенном отношении, Ь находится к а в обратном отношении.

Эквивалентность сложных суждений

На данном этапе нам предстоит изучить, что такое эквивалентные формы сложных суждений.

Рассмотрим условное суждение «если треугольник – равнобедренный, то углы у его основания равны». Утверждать это суждение, как мы уже знаем, означает утверждать, что истинность антецедента предполагает истинность консеквента, или что не может быть такого, чтобы антецедент был истинным, а консеквент – ложным. Следовательно, в данном условном суждении утверждается, что конъюнктивное суждение «треугольник является равнобедренным, и углы при его основании неравны» ложно. Или же, что строго дизъюнктивное суждение «неверно, что треугольник является равнобедренным и вместе с этим углы у его основания неравны» является истинным. Таким образом, из условного суждения мы можем вывести дизъюнкцию.

Более того, из строгой дизъюнкции мы также можем вывести условное суждение. Если дано суждение «неверно, что треугольник является равносторонним и вместе с этим углы у его основания неравны», то истинность одного дизъюнкта несовместима с истинностью другого: если один дизъюнкт истинен, другой должен быть ложным. Следовательно, из этого строго дизъюнктивного суждения мы можем вывести суждение «если треугольник является равнобедренным, то углы у его основания равны». Таким образом, может быть найдена строгая дизъюнкция, эквивалентная условному суждению.

Сказанное выше можно записать, используя введенные нами символы:

[(Треугольник является равнобедренным) ? (углы у его основания равны)] ? [(Треугольник является равнобедренным) .(углы у его основания равны)??

Из данного рассуждения также становится видно, как мы можем вывести эквивалентное условное суждение из любого другого условного суждения. Если в эквивалентной строгой дизъюнкции предполагается, что второй дизъюнкт является истинным, то первый дизъюнкт должен быть ложным. Следовательно, мы можем вывести суждение «если углы у основания треугольника неравны, то треугольник не является равнобедренным». Мы можем записать:

[(Треугольник является равнобедренным) ? (углы у его основания равны)] ? [(Углы у основания треугольника равны)??(треугольник является равнобедренным)?.

Данные эквивалентные условные суждения считаются противопоставленными (контрапозитивными) друг другу.

Рассмотрим (нестрогую) дизъюнкцию «треугольник является равнобедренным или углы у его основания равны». Утверждать данное суждение значит утверждать, что, по крайней мере, один из дизъюнктов является истинным. Поэтому, если бы один из дизъюнктов был ложным, другой должен был бы быть истинным. Следовательно, мы можем заключить из данной дизъюнкции условное суждение «если треугольник является равнобедренным, то углы у его основания равны». Более того, данная дизъюнкция может быть выведена из данного условного суждения. Это условное суждение эквивалентно суждению «неверно, что треугольник является равнобедренным и вместе с этим углы у его основания неравны», в котором утверждается, что, по крайней мере, один из дизъюнктов должен быть ложным. Из данной дизъюнкции мы можем вывести суждение «треугольник не является равнобедренным или углы у его основания равны». Мы можем записать данную эквивалентность:

[(Треугольник является равнобедренным)?? (углы у его основания равны)] ? [(Треугольник является равнобедренным) ? (углы у его основания равны)].

Из этого следует, что для любого условного суждения существует эквивалентное дизъюнктивное суждение, эквивалентное строго дизъюнктивное суждение, а также эквивалентное условное суждение. Похожее утверждение может быть сделано и относительно любого дизъюнктивного суждения и любого строго дизъюнктивного суждения. С другой стороны, конъюнкция не является эквивалентной ни одной из трех других форм сложных суждений.

Теперь приведем эквивалентные суждения для суждения «если он счастлив в браке, то он не бьет свою жену». Этими суждениями являются: «если он бьет свою жену, то он не является счастливым в браке», «он не является счастливым в браке или он не бьет свою жену» и «неверно, что он счастлив в браке и вместе с этим он бьет свою жену». В символьной записи данные суждения выглядят следующим образом:

[(Он счастлив в браке) ? (он не бьет свою жену)] ? [(Он не бьет свою жену)?? (он счастлив в браке)? ? [(Он счастлив в браке)?? (он не бьет свою жену)] ? [(Он счастлив в браке) . (он не бьет свою жену)?]?

Данные эквивалентности можно выразить более компактно, а формы эквивалентных суждений – более ясно, если принять еще некоторые конвенции относительно символов. Пусть р означает антецедент условного суждения, a q – его консеквент. Любое условное суждение может быть формализовано как ( р ? q ). Данные эквивалентности тогда могут быть записаны следующим образом:

( р ? q ) ? ( q ? ? р ?) ? ( р ?? q ) ? ( p . q ?)?

В главе VII мы рассмотрим эквивалентности между системами суждений. Однако на данном этапе можно предложить пример двух суждений, являющихся эквивалентными в силу своего места в определенной системе. Пусть р = «в физике Ньютона свет отражается от поверхности так, что угол падения равен углу отражения» и пусть q = «в физике Ньютона свет отражается от поверхности так, что его путь является минимальным». Суждения р и q эквивалентны.

Данный текст является ознакомительным фрагментом.