§ 4. Традиционный квадрат противопоставлений

§ 4. Традиционный квадрат противопоставлений

Традиционное понимание противопоставления между суждениями отличается от предложенного нами понимания. Поскольку в традиционном подходе все суждения были разложимы на субъект и предикат, противопоставлялись только суждения субъектно-предикатной формы. Противопоставление сложных суждений не рассматривалось, а описание противопоставления единичных суждений было в крайней степени неудовлетворительным.

В этом параграфе мы исследуем традиционный подход к противопоставлению. Согласно этому подходу, два суждения противопоставляются, если у них одинаковые субъект и предикат, но они отличаются по качеству, количеству или тому и другому.

Рассмотрим четыре суждения:

А. Все республики являются неблагодарными.

Е. Не одна республика не является неблагодарной.

I. Некоторые республики являются неблагодарными.

О. Некоторые республики не являются неблагодарными.

Когда мы обсуждали экзистенциальную нагруженность суждений, мы говорили, что общие суждения не требуют существования республик, тогда как частные – требуют. Следовательно, мы не можем без дальнейших допущений выводить истинность суждения типа! из истинности суждения типа А. Для того чтобы это стало возможным, нам нужно в этом параграфе раз и навсегда исследовать следствия данной гипотезы.

Среди вышеперечисленных четырех суждений нет таких двух, которые были бы независимы друг от друга или эквивалентными друг другу. Однако из возможных девяти отношений между этими суждениями мы можем усмотреть пять. Для этого удобнее использовать схематические изображения суждений.

1. Суждения «все республики являются неблагодарными» и «некоторые республики не являются неблагодарными» не могут вместе быть истинными и не могут быть вместе ложными. Из истинности одного можно обоснованно вывести ложность другого; соответственно, из ложности одного можно вывести истинность другого. Следовательно, суждения типа А и О являются противоречащими (контрадикторными). То же самое относится и к суждениям типа Е и I.

2. Суждения «все республики являются неблагодарными» и «ни одна республика не является неблагодарной» не могут вместе быть истинными. Поэтому из истинности одного из них мы могли бы вывести ложность другого. Однако если одно суждение было бы ложным, то истинностное значение другого было бы неопределенным. Следовательно, суждения типа А и Е являются противоположными (контрарными).

3. При рассмотрении суждений «все республики являются неблагодарными» и «некоторые республики являются неблагодарными» мы видим, что истинность второго суждения может быть выведена из истинности первого. Однако если первое суждение ложно, то относительно истинностного значения второго мы не можем вывести ничего. Следовательно, суждение типа А является подчиняющим по отношению к суждению типа 7, которое, в свою очередь, является подчиненным. Такое же отношение имеет место в случае с суждениями типа Е и О.

4. С другой стороны, из ложности суждения типа I можно вывести ложность суждения типа А. Однако из истинности суждения типа I мы не можем выводить истинностное значение суждения типа А. Следовательно, суждение типа I соотносится с суждением типа А как подчиненное с подчиняющим. То же самое распространяется и на суждения типа О и Е.

5. Наконец, истинность суждения «некоторые республики являются неблагодарными» совместима с истинностью суждения «некоторые республики не являются неблагодарными», однако если мы вспомним нашу договоренность считать, что слово «некоторые» не исключает понимания в смысле «все», то увидим, что не можем вывести истинность одного из этих суждений из истинности другого. Однако если какое-то из них является ложным, другое должно быть истинным. Следовательно, суждения типа I и О являются субконтрарными. Этот вывод также следует из того факта, что сужения типа А и Е являются противоположными (контрарными). А поскольку суждения типа О и I противоречат суждениям типа А и Е соответственно, и поскольку противоположные суждения не могут вместе быть истинными, то суждения типа О и I не могут вместе быть ложными. Если суждения типа А и Е могут вместе быть ложными, то суждения типа О и I могут вместе быть истинными.

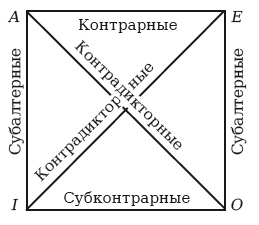
Данные отношения между категорическими суждениями были представлены в древнем квадрате противопоставлений [27] . Мы также можем построить следующую таблицу обоснованных выводов из каждого из четырех видов категорических суждений.

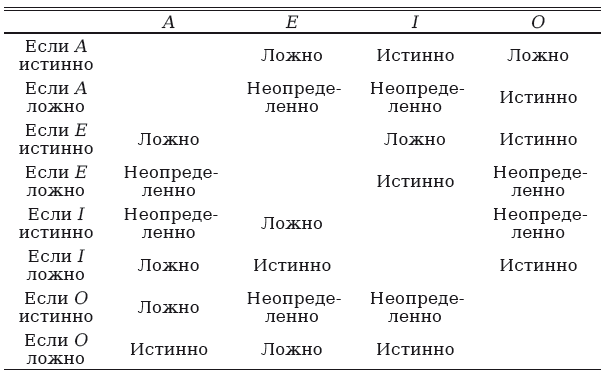
В заключение отметим, что без допущения относительно существования, которое мы сделали в начале этого параграфа, суждения типа I и О не могут быть выведены из суждений типа А и Е соответственно. Более того, без этого допущения суждения типа Л и Е не были бы противоположными, поскольку в таком случае могли бы вместе быть истинными. Так, суждения «все бессмертные люди находятся в этой комнате» и «ни один бессмертный человек не находится в этой комнате» были бы вместе истинными, если бы не существовало бессмертных людей. Однако поскольку ложно то, что существуют бессмертные люди, то (согласно интерпретации, которую мы дали частным суждениям) суждение «некоторые бессмертные люди находятся в этой комнате» и суждение «некоторые бессмертные люди не находятся в этой комнате» являются ложными. Следовательно, суждения, противоречащие данным, должны быть истинными.