2.9. Логический квадрат
2.9. Логический квадрат
Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.
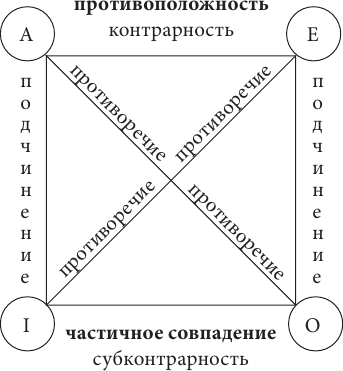
Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так если суждение вида А является истинным или ложным, то три других (I, Е, О) сравнимых с ним суждения (т. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники является истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является ложным, и суждение вида О: Некоторые тигры – это не хищники также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.
1. Если суждение вида А является истинным, то суждение вида I также является истинным, а суждения вида Е и О являются ложными.
2. Если суждение вида А является ложным, то суждение вида I является неопределенным по истинности (т. е. может быть как истинным, так и ложным, в зависимости от того, о чем будет идти в нем речь), суждение вида Е является также неопределенным по истинности, а суждение вида О является истинным. (Далее будем применять сокращения, например, вместо выражения «суждение вида А» будем говорить «А», а вместо «является истинным» – просто «истинно»).
3. Если Е истинно, то А ложно, I ложно, О истинно.
4. Если Е ложно, то А неопределенно по истинности, I истинно, О неопределенно по истинности.
5. Если I истинно, то А неопределенно по истинности, Е ложно, О неопределенно по истинности.
6. Если I ложно, то А ложно, Е истинно, О истинно.
7. Если О истинно, то А ложно, Е неопределенно по истинности, I неопределенно по истинности.
8. Если О ложно, то А истинно, Е ложно, I истинно.
Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, – по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также ложно, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
IV. Квадрат коммуникации и генеративная матрица
IV. Квадрат коммуникации и генеративная матрица Генеративная матрица высказывания проходит трехэтапный генезис и имеет четыре ключевых пункта, которые лежат на кресте пересечения двух осей - вертикальной оси Идеальности и горизонтальной оси Реальности, в результате
Исторический и логический методы
Исторический и логический методы По большому счету эмпирический уровень научного познания сам по себе не достаточен для проникновения в сущность вещей, в том числе в закономерности функционирования и развития общества. На определенном этапе, когда накоплено уже более
Логический позитивизм Карнапа
Логический позитивизм Карнапа Логический позитивизм — это видоизмененная форма эмпиризма. Эмпиризм в чистом виде — это учение о том, что все знание мы получаем из чувственного опыта. Логический позитивизм выглядит слабее его в одном важном пункте, но зато сильнее в
Головоломный квадрат
Головоломный квадрат Изображенные на рисунке двадцать кругов образуют крест. Сколько квадратов можно найти в этом кресте, если считать, что любые четыре круга являются углами квадрата? Посмотрите на схему, и вы поймете, что имеется в виду. Четыре круга с буквой А
2. Логический позитивизм
2. Логический позитивизм В 1922 году на кафедре натуральной философии Венского университета, которую после смерти Э. Маха возглавил профессор М. Шлик, собралась группа молодых ученых, поставивших перед собой смелую цель — реформировать науку и философию. Эта группа вошла
Магический квадрат
Магический квадрат Предлагаем наимоднейший способ построить так называемый «магический квадрат». Из колоды игральных карт вытащите десять одной масти — от туза (примем его за единицу) до десятки — и сложите из них квадрат. Причем сложите так, чтобы сумма чисел на
Распили квадрат
Распили квадрат В один прекрасный день Пит Распил ввалился в кафе «Ложки и плошки» и сообщил всем о головоломке, которую только что услыхал от торговца древесиной. Тот показал Питу квадратную деревянную доску с маленьким отверстием в углу. «А теперь, — сказал торговец
2. Логический обвал
2. Логический обвал — То, что может быть продемонстрировано или что требуется доказать, есть конечное познание чего-то особенного. Экзистенция и трансценденция, в смысле этого бытия, не существуют. Если мы мыслим о них, то мысль принимает логические формы, которые
14. Тетрактис и квадрат четырех[119]
14. Тетрактис и квадрат четырех[119] В ходе наших исследований нам уже не раз случалось говорить о пифагорейском Тетрактисе, и мы тогда же привели его числовую формулу: 1+2+3+4=10, указав на связь, непосредственно соединяющую денер с кватернером. Известно совершенно особое
§ 4. Традиционный квадрат противопоставлений
§ 4. Традиционный квадрат противопоставлений Традиционное понимание противопоставления между суждениями отличается от предложенного нами понимания. Поскольку в традиционном подходе все суждения были разложимы на субъект и предикат, противопоставлялись только
ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС?
ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС? Никакого исчерпывающего перечня логических парадоксов не существует. Рассмотренные логические парадоксы – это только часть из всех обнаруженных к настоящему времени. Вполне вероятно, что в будущем будут открыты и многие другие
«Квадрат ресурсов»: ищите узел проблемы
«Квадрат ресурсов»: ищите узел проблемы Если вы затрудняетесь, какие пункты и этапы вам нужно обдумать, имеет смысл воспользоваться стандартной схемой «Четыре блока успеха: Люди, МТБ (материально-техническая база), Деньги и Время». Тут имеется в виду, что для любого
Логический позитивизм
Логический позитивизм В период между первой и второй мировыми войнами были выдвинуты новые философские идеи. Многие из них были стимулированы развитием неклассической физики и стали предметом серьезного эпистемологического анализа со стороны логического позитивизма.
15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb
15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb На этом мы закончим наше краткое сообщение о применении метода бесконечно–малых к логике. Вернее, это не сообщение, а только предложение, только скромный намек на ту область, которая не может не быть огромной. Логика и математика не
Возведение в квадрат и самоусиление
Возведение в квадрат и самоусиление Есть особенно интересный вид умножения, называемый возведением в квадрат, который дает нам подсказки относительно того, как работать с нашими собственными умами. Возведение в квадрат будет очень важно позднее, когда мы будем изучать
Перевоплощение и эксперимент возведения в квадрат
Перевоплощение и эксперимент возведения в квадрат Для начала вспомните недавнее сновидение. Затем выберите из этого сновидения какую-либо фигуру – человека, дерево или что угодно еще.Теперь представьте себе, что эта фигура – основа процесса, начало ее собственной