§ 6. Специальные теоремы и правильные модусы первой фигуры

§ 6. Специальные теоремы и правильные модусы первой фигуры

Форма первой фигуры обозначается как

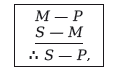
поэтому докажем следующие теоремы.

Теорема I. Меньшая посылка должна быть утвердительной. Допустим, что меньшая посылка – отрицательная. Тогда заключение должно быть отрицательным (аксиома 4), а Р должен быть распределенным. Поэтому Р должен быть распределен и в большей посылке (аксиома 2), а сама большая посылка должна быть отрицательной. Однако обе посылки не могут быть отрицательными (аксиома 3), и, следовательно, меньшая посылка должна быть утвердительной.

Теорема II. Бо?льшая посылка должна быть общим суждением.

Поскольку меньшая посылка должна быть утвердительной, ее предикат М не может быть распределенным. Поэтому М

должен быть распределен в большей посылке (аксиома 1), что, в свою очередь, делает бо?льшую посылку общим суждением.

С помощью специальной теоремы I мы можем исключить комбинации АЕ, АО, а с помощью второй теоремы – комбинации IA и ОА. В первой фигуре обоснованные заключения имеют место только в комбинациях АА, AI, ЕА и EI. Следовательно, шесть правильных модусов – это AAA, [AAI], АII, ЕАЕ, [ЕАО], ЕIO.

Модусы, обведенные нами в круг, называются подчиненными, или ослабленными, модусами, поскольку, несмотря на то что посылки в них предписывают выведение заключения, которое будет общим суждением, действительное заключение, тем не менее, является лишь частным суждением, и поэтому «более слабым», чем могло бы быть. Четырем из этих шести правильных модусов были даны специальные имена, в которых гласные соответствуют символам количества и качества посылок и заключения. Так, модус АЛА обозначается именем «Barbara», All – «Darii», ЕАЕ – «Celarent» и ЕIO – «Ferio». Данные имена были изобретены для формирования мнемонического средства, с помощью которого можно было бы вспомнить различные модусы в каждой из фигур, а модусы второй, третьей и четвертой фигур сводить к модусам первой фигуры. Ниже мы еще вернемся к проблеме сведения.