Некоторые соображения о возможности построения пространственно-метрической логики

Некоторые соображения о возможности построения пространственно-метрической логики

Ранее в этой книге (гл. IV, §2) были высказаны некие общие соображения о том, что Бейесовский силлогизм может быть реинтерпретирован в терминах метрической логики, что естественно углубляет степень геометризации развиваемой концепции и открывает новые возможности для обсуждения сверхъединой теории поля, охватывающей как семантические, так и физические проявления Вселенной.

Остановимся на этом вопросе подробнее.

Если задан силлогизм Бейеса

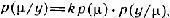
то тем самым задано преобразование весовой функции, которое в краткой символической форме можно написать:

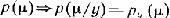
В  (1)

?( ?) — преобразуется в некоторую новую функцию ?y( ?)

При выполнении достаточно общих условий вместе с преобразованием функций имеет место преобразование соответствующих производных

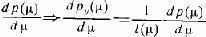
В  (2)

Здесь l( ?) — некоторая локально задаваемая (калибровочная) функция, которая определяется последним равенством, которому удобно придать несколько иную форму:

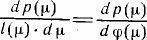
Полагая ~ ? = ?( ?) можно написать ? = ?^-1(~ ?) где ?^-1—функция обратная к функции ?. Тогда можно написать

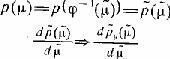
Иначе говоря, исходное преобразование (1), (2) можно выразить как преобразование индуцированное преобразованием ?-пространства ~ ? = ?( ?) которое «деформирует» метрику исходного ?-пространства, преобразуя его в ~ ?.-пространство. Отображение ~ ? = ?( ?) определяется довольно сложным образом силлогизмом Бейеса и не может быть здесь выписано явно. Важно, однако, отметить, что рассмотренные в предыдущих главах идеи в принципе могут быть изложены в терминах определенных преобразований над ?-пространством. Генератором группы этих преобразований, как ясно из сказанного, является соотношение силлогизма Бейеса.

Такой взгляд более тесно примыкает к языку современной физики, в котором фундаментальную роль играют теоретико-групповые методы.

Связанное, по сути, является указанием на некоторый язык, двойственный (сопряженный) тому, на котором велось все предыдущее изложение в книге. Подобная ситуация является довольно распространенной как в физике, так и в математике. Примерами могут служить различные представления уравнений квантовой механики, такие как Гейзенберговское представление, основанное на алгебре операторов и Шредингеровское представление, основанное на волновом уравнении [1]. Другим примером из физики могут служить теории близкодействия и дальнодействия в теории электрических и магнитных полей [2].

Примерами из математики могут служить сопряженные пространства, ковариантные и контрвариантные объекты в теории тензоров [3], теория информации и теория вероятностей (подробнее см. [4]).

Отметим здесь еще, что ВМС сближает с современной физикой представление о решающей роли наблюдателя. Текст не может быть воспринят читателем без его активного вмешательства. Воспринимаемый текст всегда должен быть реинтерпретирован. Аналогично наблюдение квантовой реальности осуществления совместно с актом неконтролируемого вмешательства наблюдателя в эту реальность [5].

Литература

В Ландау, Л. Д. и Лифшиц, Е. М. Квантовая механика.— М.: Гостехиздат, 1948.

Тамм И. Е. Основы теории электричества.— М.: Наука, 1966.

Гельфанд И. -М. Лекции по линейной алгебре.— М.: Наука, 1971.

Кульбак С. Теория информации и статистика.— М.: Наука, 1967.

Ахундов А. В. Вернер Гейзенберг и философия в кн.: Вернер Гейзенберг. Физика и философия. Часть и целое. М.: Наука, 1989.