Действительные числа

Действительные числа

Напомним, что натуральные числа являются целыми величинами:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…

Это самый элементарный и фундаментальный вид чисел. Ими можно количественно измерить любую дискретную сущность: можно говорить о двадцати семи овцах в поле, двух вспышках молнии, двенадцати ночах, тысяче слов, четырех беседах, нуле новых идей, одной ошибке, шести отсутствующих, двукратной смене направления и т. д. Натуральные числа можно складывать или перемножать, получая при этом новые натуральные числа. Мы использовали эти числа при обсуждении алгоритмов в предыдущей главе.

На самом деле при счете дат имеет место некоторое отступление от этого правила, поскольку нулевой год пропускается.

Тем не менее некоторые важные математические операции могут все же вывести нас за пределы мира натуральных чисел. Простейшая из них — вычитание. Для систематического определения вычитания нам понадобятся отрицательные числа. Теперь мы можем выстроить всю систему целых чисел:

… -6, -5, -4, -3, -2, -1, 0,

1, 2, 3, 4, 5, 6, 7…

Некоторые вещи — такие, как электрический заряд, банковские балансы или даты[58], измеряются количественно этими числами. Однако сфера применения целых чисел все же слишком ограничена, поскольку деление одного числа на другое может оказаться неразрешимой задачей в рамках целых чисел. Соответственно, нам понадобятся дроби, или, как их называют, рациональные числа:

0, 1, -1, 1/2, -1, 2, -2, 3/2, -3/2, 1/3…

Этих чисел достаточно для операций конечной арифметики, но для очень многих задач нам потребуется пойти еще дальше, с тем чтобы охватить бесконечные операции или операции перехода к пределу. Например, хорошо известная — и играющая огромную роль в математике — величина ж возникает как результат многих бесконечных выражений. В частности, мы имеем:

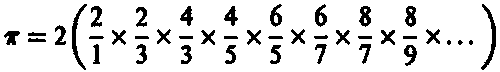
а также

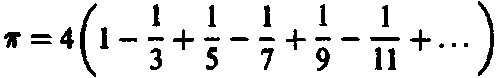
Это знаменитые выражения. Первое из них было найдено английским математиком, филологом и криптографом Джоном Уоллисом в 1655 году, а второе — шотландским математиком и астрономом (а также изобретателем первого телескопа-рефлектора) Джеймсом Грегори в 1671 году. Как и ?, определенные подобным образом числа не обязаны быть рациональными (то есть представляться в виде m/n, где m и n — целые числа, причем n не равно нулю). Систему чисел необходимо расширить, обеспечив возможность включения в нее таких величин.

Расширенная таким образом система чисел называется системой действительных чисел — тех самых хорошо знакомых нам чисел, что представляются в виде бесконечных десятичных дробей, таких как:

?583,70264439121009538…

В этом представлении мы получаем следующее известное выражение для числа ?:

? = 3,14159265358979323846….

Другими примерами чисел, представимых таким образом, являются квадратные корни (или кубические корни, или корни четвертой степени) из положительных рациональных чисел, такие как:

?2= 1,41421356237309504…

или же квадратные корни (или кубические корни и т. д.) любого положительного числа, как, например, выражение для числа ?, найденное великим швейцарским математиком Леонардом Эйлером:

? = ?6 (1 + 1/4 + 1/9 + 1/25 + 1/36 +…).

Действительные числа нам в сущности хорошо знакомы — мы с ними сталкиваемся в повседневной жизни. Правда обычно нас интересуют всего лишь приближения к этим числам и мы предпочитаем ограничиваться разложениями, состоящими из небольшого числа десятичных знаков. Тем не менее, в математических утверждениях может потребоваться точное задание действительных чисел и, как следствие, необходимость в некотором бесконечном способе описания наподобие бесконечной десятичной дроби, или какого-нибудь иного бесконечного математического выражения вроде приведенных выше формул для числа ?, предложенных Уоллисом, Грегори и Эйлером. (В дальнейшем я буду обычно использовать десятичные дроби, но лишь потому, что они нам наиболее привычны. У математиков есть множество разных и более удовлетворительных способов представления действительных чисел, но нас это здесь не интересует.)

Может создаться впечатление, что представить себе все бесконечное десятичное разложение целиком невозможно, но это не так. Вот простой пример, когда вся последовательность знаков оказывается явным образом обозримой:

1/3 = 0,333333333333333…

Многоточие указывает на то, что последовательность троек продолжается бесконечно. Для получения полного представления об этом разложении достаточно знать, что оно действительно состоит из неограниченной последовательности одних лишь троек. У каждого рационального числа есть повторяющееся (или конечное) десятичное представление вроде:

93/74 = 1,2567567567567567…,

где последовательность 567 повторяется неограниченное число раз. Это число тоже оказывается полностью обозримым. Также обозримым является выражение

0,220002222000002222220000000222222220…

которое определяет иррациональное число (оно просто состоит из последовательностей нулей и двоек, длины которых каждый раз увеличиваются на единицу), и еще много похожих выражений. В каждом таком случае нам достаточно знать правило, по которому составлено разложение. Знание алгоритма порождения очередной цифры в разложении числа — при условии, что такой алгоритм существует — дает нам способ «увидеть» целиком все бесконечное десятичное разложение. Действительные числа с алгоритмически порождаемыми десятичными разложениями называются вычислимыми числами (см. также гл.2 «Числа, отличные от натуральных»). (При этом не важно, десятичное это разложение или двоичное. Вычислимыми в этом смысле оказываются одни и те же числа, независимо от использованного основания разложения.) Только что рассмотренные числа ? и ?2 представляют собой примеры вычислимых чисел. В обоих случаях подробное описание соответствующего правила — задача довольно-таки кропотливая, но, в принципе, нетрудная.

Есть, однако, действительные числа, которые не являются вычислимыми в упомянутом выше смысле. Как мы убедились в главе 2, существуют невычислимые и при этом совершенно четко определенные последовательности. В качестве примера можно рассмотреть десятичное разложение, в котором n-я цифра равна 0 или 1 в зависимости от того, останавливается или нет n-я машина Тьюринга, производящая действия над числом n. В общем случае мы потребуем лишь, чтобы для действительного числа существовало какое-нибудь бесконечное десятичное разложение. Мы не только не требуем существования алгоритма порождения n-й цифры, но нам даже не обязательно знать о существовании какого бы то ни было правила, в принципе определяющего n-ю цифру[59]. Заметим, что вычислимые числа неудобны в работе. Невозможно обойтись одними лишь вычислимыми операциями, даже оперируя вычислимыми числами. Например, в общем случае вычислимым образом невозможно даже решить, равны ли два вычислимых числа друг другу! По этой причине мы будем работать со всеми действительными числами, когда десятичная последовательность может быть любой, а не только, скажем, вычислимой.

В заключение отметим также тождественность действительных чисел, чьи десятичные разложения заканчиваются бесконечной последовательностью девяток, и чисел, чьи разложения заканчиваются бесконечной последовательностью нулей. Например:

— 27,1860999999… = -27,1861000000…

Данный текст является ознакомительным фрагментом.