«Действительность» действительных чисел

«Действительность» действительных чисел

Если отвлечься от понятия вычислимости, то действительные числа называются «действительными», потому что они, как представляется, дают величины, необходимые для измерения расстояний, углов, времени, энергии, температуры и многих других геометрических и физических параметров. Однако связь абстрактно определенных «действительных» чисел с физическими величинами не так проста, как может показаться. Действительные числа следует рассматривать скорее как некоторую математическую идеализацию, чем как реальную меру физически объективных величин. Система действительных чисел обладает, например, таким свойством, что между любыми двумя действительными числами (вне зависимости от их близости) существует третье действительное число. При этом совершенно не ясно, можно ли обоснованно утверждать то же самое о физических расстояниях или промежутках времени. Если мы продолжим дробить физическое расстояние между двумя точками, то мы в конце концов достигнем масштабов столь малых, что само понятие расстояния в обычном его смысле станет бессмысленным. Предполагается, что это действительно имеет место на масштабах, характерных для квантовой теории гравитации, которые в 10²⁰ раз[61] меньше размеров субатомных частиц. Но чтобы отобразить действительные числа нам потребуется дойти до сколь угодно более мелких масштабов, которые, например, в 10²⁰⁰, 10²⁰⁰⁰ или даже в

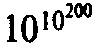
раз меньше размеров частиц. И совершенно не ясно, есть ли какой бы то ни было физический смысл у столь абсурдно малых масштабов. То же самое можно сказать и в отношении столь же малых интервалов времени.

Система действительных чисел выбрана в физике в силу ее математической полезности, простоты и изящества, а также поскольку она согласуется на очень широком интервале масштабов с физическими понятиями пространства и времени. Она выбрана не потому, что мы будто бы знаем, что она согласуется с упомянутыми физическими величинами на всех масштабах. Такое согласие вполне может не иметь места на очень малых пространственных и временны?х масштабах. Обычные расстояния измеряются при помощи линейки, но линейка оказывается «зернистой» при переходе к масштабам образующих ее атомов. Само по себе это не мешает нам продолжать использовать действительные числа подходящим образом, но измерение меньших расстояний требует уже гораздо большей изобретательности. По крайней мере, мы должны быть готовы предположить, что на очень-очень малых масштабах могут встречаться принципиальные трудности с расстояниями. Как оказывается, природа оказалась к нам на удивление благосклонна, сделав те самые действительные числа, которые мы привыкли повседневно применять для описания предметов на макромасштабах, пригодными для описания расстояний гораздо меньших атомных — по крайней мере, на масштабах, равных одной сотой «классического» диаметра элементарной частицы — такой, как электрон или протон, — и, по-видимому, вплоть до «масштабов квантовой теории гравитации», что на двадцать порядков меньше размеров таких частиц! Это пример исключительно сильной экстраполяции нашего опыта. Сфера применимости привычного понятия расстояния, измеряемого действительными числами, по-видимому, простирается до самых далеких квазаров и еще дальше. Общий диапазон измеримых расстояний составляет 10⁴², а может быть, 10⁶⁰ или даже больше. Кстати, сомнения в правомерности использования системы действительных чисел высказывались не так уж часто. Почему же мы так уверены в том, что эти числа дают точное описание физических явлений, хотя реально об их применимости мы знаем лишь в весьма ограниченном диапазоне масштабов? Должно быть, эта уверенность — возможно, неверная — основывается на (правда, не очень часто признаваемых) логическом изяществе, внутренней согласованности и математической мощи системы действительных чисел в сочетании с верой в глубинную математическую гармонию природы.