Рекурсивно нумеруемые множества
Рекурсивно нумеруемые множества
Существует способ для описания основных результатов, полученных Геделем и Тьюрингом, в графическом виде, на языке теории множеств. Это позволит нам избежать произвольности описания в терминах конкретного символизма или в рамках формальной системы и выделить наиболее существенное. Мы будем рассматривать только множества натуральных чисел (конечные или бесконечные), такие как {4,5,8}, {0,57,100003}, {6}, {0}, {1,2,3,4….,9999}, {1,2, 3,4…. }, {0,2,4,6,8…. } ит. п.; или даже все множество N = {0,1,2,3,4… }, равно как и пустое множество ? = {}. Нас будут интересовать только вопросы вычислимости, скажем: «Какие множества натуральных чисел могут быть сгенерированы с помощью алгоритма, а какие — нет?»
Чтобы сформулировать такой вопрос, мы можем считать, что каждое отдельное число n обозначает определенную строчку символов некоторой формальной системы.
Это будет n-я строка символов, скажем, Qn, согласно заданному в системе лексикографическому порядку («синтаксически корректных») утверждений. Тогда каждое натуральное число будет представлять некое утверждение. При этом множество всех утверждений формальной системы соответствует всему множеству натуральных чисел; а, допустим, теоремы этой системы будут составлять некоторое меньшее множество натуральных чисел, скажем, множество Р. Однако детали произвольной системы нумерации утверждений для нас несущественны. Все, что нам потребуется для установления соответствия между натуральными числами и утверждениями — это заданный алгоритм получения каждого утверждения Qn (записанного должным образом в символических обозначениях) из отвечающего ему натурального числа n; и другой алгоритм для получения n из Qn. Имея эти алгоритмы в своем распоряжении, мы вольны идентифицировать множество натуральных чисел с множеством утверждений конкретной формальной системы.
Давайте выберем формальную систему достаточно непротиворечивую и широкую для того, чтобы включать в себя все действия всех машин Тьюринга — и, более того, «имеющую смысл» с учетом требования «самоочевидной справедливости» ее аксиом и правил вывода. Далее, пусть ряд утверждений Q0, Q1, Q2…. формальной системы имеет доказательства внутри системы. Эти «доказуемые» утверждения будут иметь номера, которые составляют некоторое множество в N — по сути, это множество Р «теорем», рассмотренных выше. Мы уже видели, что существует алгоритм для последовательного построения всех утверждений произвольно заданной формальной системы, имеющих доказательства. (Как отмечено ранее, «n-е доказательство» Пn получается из n алгоритмически. Все, что нам надо — это посмотреть на последнюю строчку n-го доказательства, чтобы найти «n-е утверждение, доказуемое в рамках системы», т. е. n-ю «теорему».) Следовательно, мы имеем алгоритм последовательной генерации элементов Р (при которой возможны и повторения, что для нас не важно).
Множество типа Р, которое может быть построено с помощью некоторого алгоритма, называется рекурсивно нумеруемым. Заметьте, что множество утверждений, ложность которых может быть установлена в рамках системы — т. е. утверждений, чьи отрицания являются справедливыми — точно так же рекурсивно нумеруемо, поэтому мы можем просто нумеровать доказуемые утверждения по мере продвижения, учитывая и их отрицания. Есть большое число других, тоже рекурсивно нумеруемых, подмножеств N, для определения которых нам вовсе необязательно ссылаться на нашу формальную систему. Простыми примерами рекурсивно нумеруемых множеств могут служить множество четных чисел
{О, 2,4,6, 8…. }, множество квадратов
{0,1,4,9,16….} и множество простых чисел
{2,3,5, 7, И….}.
Очевидно, мы можем построить любое из этих множеств при помощи алгоритма. Для каждого из этих трех примеров будет справедливо следующее свойство: дополнительное по отношению к рассматриваемому множество (состоящее из всех натуральных чисел, не входящих в исходное множество) является также рекурсивно нумеруемым. Дополнительными по отношению к вышеприведенным множествам будут, соответственно:
{1,3,5,7,9….}, {2,3,5,6,7,8,10….}
и
{0,1,4,6, 8,9,10,12….}.
Было бы достаточно просто указать алгоритм и для этих дополнительных множеств. Конечно же, мы можем выяснить алгоритмическим путем, является ли произвольное натуральное число n четным, квадратом натурального числа или простым числом, соответственно. Это дает нам алгоритм для построения обоих множеств, поскольку мы можем перебирать все натуральные числа и для каждого из них решать, принадлежит ли оно к определенному множеству или же к его дополнению. Множество, которое обладает свойством рекурсивной нумеруемости вместе со своим дополнением, называется рекурсивным. Очевидно, что дополнительное по отношению к рекурсивному множество также будет рекурсивным.
А существуют ли множества, которые рекурсивно нумеруемы, но рекурсивными, тем не менее, не являются? Давайте на минутку задумаемся над тем, какие следствия могут вытекать из подобного свойства. Поскольку элементы такого множества могут быть получены алгоритмическим путем, мы имели бы способ решить, принадлежит ли некоторый элемент — который, мы предполагаем, да, принадлежит множеству, — рассматриваемому множеству или нет. Все, что от нас требуется, — это запустить алгоритм и прогонять его через все элементы множества до тех пор, пока он не найдет элемент, который мы ищем. Теперь давайте предположим, что искомый элемент не принадлежит данному множеству. В таком случае использование нашего алгоритма ничего не даст: он будет работать вечно, будучи не в состоянии прийти к решению. В этом случае нам потребуется алгоритм для построения дополнительного по отношению к исходному множества. Если этот алгоритм сможет обнаружить искомый элемент, то мы будем точно знать, что он не входит в состав исследуемого множества. Имея на вооружении оба алгоритма, мы так или иначе найдем данный элемент путем поочередного применения этих алгоритмов. Однако, такой благоприятный исход будет иметь место только в случае рекурсивного множества. Мы же предполагаем, что мы рассматриваем множество рекурсивно нумеруемое, но при этом не рекурсивное, т. е. наш предполагаемый алгоритм для построения дополнительного множества просто не существует! Таким образом, мы имеем курьезную ситуацию, когда можно определить, включен ли элемент в множество при условии, что он ему наверняка принадлежит; но в то же время нельзя гарантировать, что мы сможем это сделать посредством какого бы то ни было алгоритма для элементов, которые множеству не принадлежат.
Может ли возникнуть такая ситуация в реальности? Есть ли и вправду рекурсивно нумеруемые множества, не являющиеся рекурсивными? А как насчет множества Р ? Имеет ли это множество свойство рекурсивности? Мы знаем, что оно рекурсивно нумеруемо, так что нам остается только выяснить, будет ли также дополнительное к нему множество обладать этим свойством. Оказывается, что нет! Как мы можем сделать такой вывод? А давайте вспомним, что наряду с остальными операциями в нашей формальной системе разрешены и действия машин Тьюринга. Если мы обозначим n-ю машину Тьюринга через Тn то выражение
«Тn(n) останавливается»
— это утверждение — запишем его как S(n), — которое мы можем сформулировать в рамках нашей системы для любого n. Утверждение S(n) будет справедливым для одних значений n, и ложным — для остальных. Множество всех S(n), образованное перебором натуральных чисел 0,1, 2, 3…., будет представлено некоторым подмножеством N — скажем, S. Теперь учтем фундаментальный результат Тьюринга (глава 2, «Неразрешимость проблемы Гильберта»), который говорит о том, что не существует алгоритма, способного установить факт «Тn(n) не останавливается» как раз в тех случаях, когда она действительно не останавливается. Это означает, что множество, состоящее из отрицаний S(n), не является рекурсивно нумеруемым.
Мы видим, что часть S, принадлежащая Р, состоит только из истинных S(n). Почему это так? Понятно, что если любое конкретное S(n) доказуемо, то оно должно быть верным (ведь наша формальная система была выбрана так, чтобы иметь «смысл»!), и поэтому часть S, лежащая в Р, должна состоять исключительно из справедливых утверждений S(n). Более того, ни одно верное утверждение S(n) не должно лежать вне Р, ибо, если Тn (n) останавливается, то мы можем отыскать доказательство этому в рамках нашей системы[82].
Теперь предположим, что дополнение Р рекурсивно нумеруемо. Тогда у нас был бы алгоритм для построения элементов этого дополнительного множества. И мы смогли бы запустить его и пометить каждое утверждение S(n), которое попадает в поле его действия. Это все будут ложные утверждения S(n), так что наша процедура, по сути, обеспечит нам рекурсивную нумерацию множества таких утверждений. Но выше мы установили, что это множество не нумеруемо таким образом. Это противоречие показывает, что дополнение Р все-таки не может быть рекурсивно пронумеровано; а Р, следовательно, не является рекурсивным, что и требовалось доказать.
Эти свойства с очевидностью демонстрируют, что наша формальная система не может быть полной: то есть всегда будут существовать утверждения, чью справедливость (или ложность) невозможно доказать в рамках системы. Ведь если предположить, что такие «неразрешимые» утверждения не существуют, то дополнение множества Р с необходимостью было бы множеством опровергаемых утверждений (все, что недоказуемо, обязано быть опровергаемо). Но мы уже знаем, что опровергаемые утверждения составляют рекурсивно нумеруемое множество, что делает Р рекурсивным. Однако, Р не рекурсивно — противоречие, которое доказывает требуемую неполноту. Это основное утверждение теоремы Геделя.
А как насчет подмножества T множества N, которое состоит из истинных утверждений нашей формальной системы? Рекурсивно ли T? Или оно только рекурсивно нумеруемо? А его дополнение? Оказывается, что ответ на все эти вопросы — отрицательный. Один из способов установить это — воспользоваться сделанным ранее выводом о невозможности алгоритмически сгенерировать ложные утверждения вида «Тn(n) останавливается». Как следствие, ложные утверждения в целом не могут быть получены с помощью алгоритма, поскольку такой алгоритм, в частности, пронумеровал бы все вышеупомянутые ложные «Тn(n) останавливается»-утверждения. Аналогично, и множество всех истинных утверждений не может быть построено при помощи алгоритма (так как любой подобный алгоритм легко модифицируется для нахождения ложных утверждений путем отрицания каждого из генерируемых им утверждений).
Поскольку, тем самым, истинные утверждения не являются (равно как и ложные) рекурсивно нумеруемыми, то они образуют гораздо более глубокий и сложноорганизованный массив, чем утверждения, имеющие доказательство внутри системы. И это иллюстрирует еще один аспект теоремы Геделя: что понятие математической истины только частично досягаемо в рамках любой формальной системы.
Существуют некоторые простые классы истинных арифметических утверждений, которые все же образуют рекурсивно нумеруемые множества. Например, как это нетрудно видеть, истинные утверждения вида
Eк.с. ?, x…, z[f (?, x,…,z) = 0],
где f () — некоторая функция, построенная из обычных арифметических операций сложения, вычитания, умножения и возведения в степень, составляют рекурсивно нумеруемые множества[83] (которые я обозначу через А). Пример утверждения такого рода — хотя мы не знаем, верно ли оно — это отрицание последней теоремы Ферма[84]., для которой мы можем взять за f () функцию
f (?, х, у, z) = (х+1)?+3 + (у+1)?+3- (z+1)?+3.
Однако, множество А не является рекурсивным (факт, который не так легко установить, хотя он и вытекает из оригинального доказательства Геделя). Значит, мы не имеем никаких алгоритмических средств для выяснения — хотя бы в принципе — истинности или ложности последней теоремы Ферма.

Рис. 4.1. Очень схематичное представление рекурсивного множества
На рис. 4.1 я попытался схематически представить рекурсивное множество как фигуру с простой и изящной границей, так что кажется, что определить непосредственно принадлежность произвольной точки этому множеству — дело несложное. Каждая точка на рисунке соответствует некоторому натуральному числу. При этом дополнительное множество также представлено в виде просто выглядящей области на плоскости. На рис. 4.2 я постарался изобразить рекурсивно нумеруемое, но не рекурсивное множество в виде области со сложной границей, где подразумевается, что множество с одной стороны границы, — той, что рекурсивно нумеруема — должно выглядеть проще, чем с другой.

Рис. 4.2. Очень схематичное представление рекурсивно нумеруемого множества (темная область), которое не является рекурсивным. Здесь светлая область определяется только по «остаточному принципу», когда удаляется темная часть, построенная при помощи вычислений; а установить путем прямых вычислений, принадлежит ли заданная точка белой области, нельзя
Фигуры очень схематичны и не претендуют на какую бы то ни было «геометрическую аккуратность». И конечно же, не стоит придавать большого значения тому, что эти рисунки изображены так, как если бы они были расположены на двумерной плоскости!
На рис. 4.3 я схематично обозначил, как расположены области Р, Т и А внутри множества N.
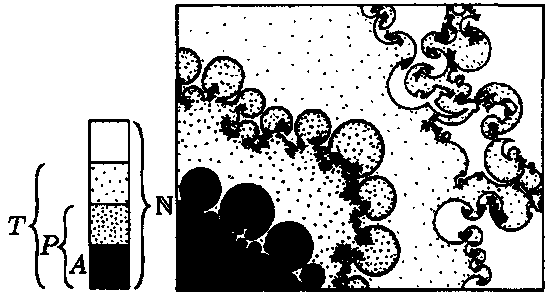
Рис. 4.3. Очень схематичное представление различных множеств утверждений. Множество Р утверждений, доказуемых в рамках системы, является, как и А, рекурсивно нумеруемым, но не рекурсивным. Множество Т истинных утверждений даже не рекурсивно нумеруемо
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Глава 10. Наука является одной из множества идеологий и ее следует отделить от государства так, как ныне отделена от него Церковь
Глава 10. Наука является одной из множества идеологий и ее следует отделить от государства так, как ныне отделена от него Церковь Я начал с утверждения о том, что свободным является такое общество, в котором все традиции обладают равными правами и равным доступом к центрам
Два множества и один пример
Два множества и один пример Два множества, о которых мне хочется сказать здесь, это множестве литературных произведений и множество критики на них. Гетерогенность первого — просто трюизм. Разные произведения построены по разным принципам. Но тогда, может быть, не лишен
Метод двадцатого века заключается в использовании не одной, а множества моделей экспериментального исследования, т. е. техники «подвешенного» суждения
Метод двадцатого века заключается в использовании не одной, а множества моделей экспериментального исследования, т. е. техники «подвешенного» суждения Уильям Айвинз младший в книге «Эстампы и визуальная коммуникация» подчеркивает (р.63), что в мире письменного слова
1. ] Народ против Множества: Гоббс и Спиноза
1. ] Народ против Множества: Гоббс и Спиноза Я считаю, что понятие «множества» (moltitudine), противопоставляемое более привычному понятию «народ», является необходимым орудием при любом размышлении по поводу современной публичной сферы. Необходимо иметь в виду, что
3] Эмоциональные тональности множества
3] Эмоциональные тональности множества Сейчас я хотел бы коротко порассуждать об эмоциональной ситуации, в которой находится современное множество. Используя выражение «эмоциональная ситуация», я имею в виду, конечно, не набор психологических склонностей, а настолько
IV.] Разработка понятия множества
IV.] Разработка понятия множества «Грамматика» у Вирно означает процедуру формирования понятия множества через его встраивание как «подлежащего» в различные «предложения» и контексты как современного социального опыта, так и философии — от Аристотеля, Гоббса, Канта и
6.2.3. Особая вселенная, выделенная из множества, или мультивселенная
6.2.3. Особая вселенная, выделенная из множества, или мультивселенная Для тех, кто не верит в замысел провидения, но все же полагает, что тонкая «настройка» требует какого?то объяснения, есть еще одна перспектива, правда, чисто спекулятивная. Возможно, существует множество
1. Общество как едино-цельная система определенного множества народа
1. Общество как едино-цельная система определенного множества народа Общество и сообщество. Общество являет собой некое единое целое, состоящее из людей, связанных различной степенью общности, что позволяет назвать их совместностью, а это возможно лишь на достаточно