Насколько особым был Большой взрыв?

Насколько особым был Большой взрыв?

Попробуем разобраться с вопросом о том, насколько ограничивающим для Большого взрыва было условие типа ВЕЙЛЬ = 0. Для простоты (как и ранее) мы будем считать вселенную замкнутой. Для того чтобы составить ясную и конкретную картину, далее мы везде будем полагать, что число барионов В — т. е. общее число протонов и нейтронов, во вселенной составляет примерно

В = 10⁸⁰.

(Не существует каких-то особых оснований для выбора именно этого значения, кроме тех эмпирических данных, которые приводят к нему как к нижней оценке В. Эддингтон однажды заявил, что вычислил В точно и полученное им значение оказалось близким к приведенному выше! Кажется, что сейчас уже никто не принимает всерьез эти вычисления, но значение 10⁸⁰ надежно утвердилось.) Если бы мы взяли большее значение В (в действительности может оказаться, что ВЕЙЛЬ ? ?), то величины, полученные нами в этом случае, оказалась бы еще поразительнее тех (и без того весьма экстраординарных чисел), к которым мы через несколько шагов придем!

Попробуем представить себе фазовое пространство (Глава 5. «Фазовое пространство») всей вселенной! Каждая точка этого пространства потенциально соответствует определенному начальному состоянию, из которого вселенная могла начинать свою эволюцию. На рис. 7.19 мы условно изображаем Творца, который в своей деснице держит «булавку», чтобы отметить ею некую точку нашего фазового пространства.

Рис. 7.19. Для сотворения вселенной, близкой по своим свойствам к той, в которой мы живем, Творец ограничивает свой выбор исчезающе малым объемом в фазовом пространстве возможных вселенных, в рассматриваемом случае — всего около 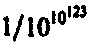объема всего пространства. (Этот объем и нацеленная на него булавка показаны без соблюдения масштабов!)

Каждое положение булавки соответствует творению особой вселенной. Точность, с которой Творец создает какую-либо вселенную, напрямую связана с энтропией этой вселенной. Создать вселенную с высокой энтропией было бы относительно «легко», поскольку в этом случае в распоряжении Творца имеется большой объем фазового пространства, в который надо указать булавкой. (Напомним, что энтропия пропорциональна логарифму объема соответствующего фазового пространства.) Но чтобы создать вселенную в состоянии с низкой энтропией — так, чтобы в ней выполнялось второе начало термодинамики, — Творец должен направить булавку в гораздо меньший объем фазового пространства. Насколько малым должен быть этот объем, чтобы в результате творения получилась вселенная, напоминающая по своим свойствам ту, в которой мы живем? Для ответа на этот вопрос, мы должны обратиться к замечательной формуле, выведенной Якобом Бекенштейном [1972] и Стивеном Хокингом [1975], которая говорит о том, чему должна быть равна энтропия черной дыры.

Рассмотрим черную дыру и допустим, что площадь ее горизонта есть А. Формула Хокинга-Бекенштейна для энтропии черной дыры гласит:

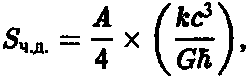
где k — константа Больцмана, с — скорость света, G — ньютоновская гравитационная постоянная и ? — постоянная Планка, деленная на 2?. Самая существенная часть этой формулы заключена во множителе А/4. Часть, стоящая в скобках, содержит только необходимые для соблюдения размерности физические константы. Таким образом, энтропия черной дыры оказывается пропорциональной площади ее поверхности. Для сферически симметричной черной дыры эта площадь оказывается пропорциональной квадрату массы этой дыры:

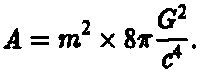
Объединяя это с формулой Бекенштейна — Хокинга, мы получаем, что энтропия черной дыры пропорциональна квадрату ее массы:

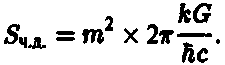
Таким образом, энтропия, приходящаяся на единицу массы (S_ч.д./m) черной дыры, пропорциональна ее массе и оказывается тем больше, чем больше черная дыра. Следовательно, для заданной массы или, эквивалентно, — согласно формуле Эйнштейна Е = mc², — для заданной энергии, наибольшая энтропия достигается тогда, когда вся материя сколлапсирует в черную дыру! Более того, энтропия системы двух черных дыр существенно возрастает, когда эти дыры сливаются в одну! Гигантские черные дыры, типа тех, которые, как полагают, находятся в центрах галактик, заключают в себе колоссальное количество энтропии — намного превосходящее те ее значения, которые встречаются в других физических ситуациях.

Утверждение о том, что максимум энтропии достигается при коллапсе всей массы в черную дыру, требует небольшого пояснения. Анализ термодинамики черных дыр, проведенный Хокингом, показывает, что с любой черной дырой можно связать некоторую ненулевую температуру. Одним из следствий этого является тот факт, что в состоянии с максимальной энтропией в черной дыре не может быть заключена вся масса-энергия; максимум энтропии достигается, когда черная дыра приходит в тепловое равновесие с «тепловым резервуаром излучения». Температура этого излучения оказывается действительно ничтожной для черных дыр с любым разумным размером. Так, к примеру, для черной дыры с массой порядка массы Солнца эта температура оказалась бы равной примерно 10 ^-7 К, что значительно ниже температур, достигнутых в настоящее время в лабораториях, и намного меньше температуры 2,7 К межгалактического пространства. Для черных дыр больших размеров температура Хокинга оказывается еще меньшей!

Эта температура могла бы оказаться существенной для нашего обсуждения только в том случае, если либо (а) во вселенной существуют намного меньшие черные дыры, которые называют черными мини-дырами; либо (б) вселенная не успеет полностью сколлапсировать за время, меньшее хокинговского времени испарения — времени, за которое черная дыра полностью испаряется. Относительно (а) надо заметить, что черные мини-дыры могут возникнуть лишь в случае особенно хаотичного Большого взрыва. В нашей вселенной их не может быть очень много, в противном случае они бы уже как-то проявили бы себя; более того, согласно излагаемой мной здесь точки зрения, их вообще не должно быть.

Что же касается (б), то для черной дыры с солнечной массой хокинговское время испарения имело бы величину, превосходящую нынешний возраст вселенной где-то в 10⁵⁴; а для черных дыр бо?льших размеров оно оказалось бы еще более продолжительным. Таким образом, вряд ли эффект испарения может существенно изменить наши предыдущие рассуждения.

Чтобы иметь некоторое представление о гигантских величинах энтропии черных дыр, рассмотрим чернотельное фоновое излучение с температурой 2,7 К, которое, как долго казалось, давало наибольший вклад в энтропию вселенной. Астрофизики были просто ошарашены огромным количеством энтропии, заключенным в этом излучении, которое намного превосходило все значения энтропии, с которыми приходилось сталкиваться в других ситуациях (например, на Солнце). Энтропия фонового излучения составляет примерно 10⁸ на один барион (здесь я снова перехожу к «естественной системе единиц», в которых постоянная Больцмана равна единице). (По сути, это означает, что на каждый барион приходится 10⁸ фотонов фонового излучения.) Таким образом, если всего имеется 10⁸⁰ барионов, то для полной энтропии фонового излучения во вселенной мы имели бы величину

10⁸⁸.

Несомненно, что если бы не было черных дыр, то эта величина представляла бы собой практически всю энтропию вселенной, поскольку энтропия фонового излучения намного превосходит энтропию всех других обычных процессов. Так, например, энтропия, приходящаяся на один барион на Солнце, оказывается порядка единицы. С другой стороны, по меркам черных дыр, энтропия фонового излучения — это просто «писк комара». Для черной дыры в одну солнечную массу формула Бекенштейна— Хокинга дает нам значение энтропии около 10²⁰ на один барион (в естественных единицах). И даже если бы вселенная состояла всего-навсего из одной черной дыры с массой Солнца, полная энтропия оказалась бы уже намного превосходящей приведенное ранее значение, а именно, была бы равной

10¹⁰⁰.

Конечно, вселенная не устроена таким образом, но эта цифра определенно свидетельствует о том, насколько несущественной становится энтропия фонового излучения, когда мы начинаем учитывать влияние вездесущей гравитации.

А теперь попробуем сделать более реалистичную оценку. Вместо того, чтобы заселять наши галактики одними только черными дырами, примем, что эти галактики состоят, в основном, из обычных звезд — примерно 10¹¹ штук в каждой и еще содержат в своей сердцевине около миллиона (10⁶) черных дыр с массой солнца (что было бы вполне правдоподобно для нашей собственной Галактики — Млечного Пути). Вычисления показывают, что энтропия, приходящаяся на один барион, оказалась бы в этом случае существенно больше даже того огромного значения, которое было только что получено — она стала бы равной 10²¹, что для полной энтропии дает (в естественных единицах) величину, равную примерно

10¹⁰¹.

Мы можем предположить, что, по истечении достаточно большого промежутка времени, подавляющая часть галактических масс окажется захваченной черными дырами в центрах галактик. Когда это произойдет, энтропия в расчете на один барион станет равной 10³¹, что дает чудовищное значение для полной энтропии:

10¹¹¹.

Мы, однако, рассматриваем замкнутую вселенную, которая, в конце концов, должна сколлапсировать; и было бы вполне разумно оценить энтропию конечного коллапса, используя формулу Бекенштейна — Хокинга и полагая при этом, что вся вселенная в момент коллапса представляет собой одну черную дыру. Такая оценка дает величину энтропии на один барион около 10⁴³ и совершенно немыслимую величину полной энтропии для конечного коллапса:

10¹²³.

Это число мы будем рассматривать как некоторую оценку полного объема фазового пространства V, доступного для Творца, поскольку эта энтропия должна представлять собой логарифм объема (несомненно) наибольшей его части. Поскольку 10¹²³ есть логарифм объема, сам объем должен представлять собой экспоненту от 10¹²³, т. е.

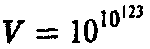
в естественных единицах! (Некоторые особо внимательные читатели могли заметить, что я должен был написать

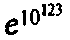
— но для чисел такого порядка разница между основаниями е и 10 совершенно несущественна!) А каков был исходный объем фазового пространства, на который должен был нацелиться Творец, чтобы сотворить вселенную, совместимую со вторым началом термодинамики? Оказывается, что совершенно не важно, какое выбрать значение

определяемое галактическими черными дырами или фоновым излучением соответственно, а, может быть, даже еще меньшее (и, на самом деле, более вероятное), которое могло иметь место в реальных условиях при Большом взрыве.

В любом случае, значение отношения V к W будет приблизительно:

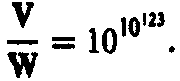
(Проверьте сами:

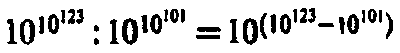
дает с хорошим приближением

.)

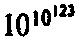
Эта величина свидетельствует о том, насколько точным должен был быть замысел Творца: точность составляла примерно одну

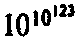
— ую! Это поразительная точность. Полученную цифру нельзя даже полностью выписать в обычной десятичной системе исчисления: она представляла бы собой «1» с последующими 10¹²³ нулями! Даже если бы мы были в состоянии записать «0» на каждом протоне и каждом нейтроне во вселенной, а также использовали бы для этой цели все остальные частицы, наше число, тем не менее, осталось бы недописанным.

Точность, необходимая для задания начальных условий вселенной, как видно, совершенно несоизмерима с той весьма высокой точностью, которая уже стала привычной, когда речь заходит о динамических уравнениях (Ньютона, Максвелла, Эйнштейна), управляющих поведением физических объектов в различных ситуациях.

Но почему же Большой взрыв был организован с такой высокой степенью точности, в то время как большой коллапс (или сингулярности черных дыр) должен быть совершенно хаотичным? Может показаться, что этот вопрос стоило бы переформулировать в терминах поведения ВЕЙЛЬ-части пространственно-временно?й кривизны в пространственно-временно?й сингулярности. Мы установили, что имеется ограничение

ВЕЙЛЬ = 0

(или нечто похожее) в сингулярностях начального типа, отсутствующее в конечных сингулярностях — и, кажется, именно оно отражает выбор Творцом соответствующей крошечной области фазового пространства. Предположение о том, что такое ограничение применимо к любой начальной (но не конечной!) сингулярности, я назвал бы Гипотезой Вейлевской Кривизны. Таким образом, напрашивается вывод, что нам осталось понять лишь одну вещь для окончательного разрешения вопроса о происхождении второго начала термодинамики, а именно: почему мы должны использовать такую несимметричную во времени гипотезу?[187]

Но как нам преодолеть это (последнее?) препятствие на пути к полному пониманию причины существования второго начала? Кажется, мы попали в безвыходное положение. Нам необходимо понять, почему пространственно-временны?е сингулярности имеют определенную структуру; но пространственно-временны?е сингулярности представляют собой как раз те области, в которых наше понимание физики достигает своих пределов. Этот тупик, связанный с существованием пространственно-временны?х сингулярностей, иногда сравнивают с другим тупиком: он имел место в начале XX века и был связан с проблемой устойчивости атомов (см.: Главу 6. «Проблемы с классической теорией»). В каждом из этих случаев хорошо обоснованная классическая теория приводит к ответу «бесконечность» и обнаруживает, тем самым, свою несостоятельность для решения соответствующей проблемы.

Сингулярный характер электромагнитного коллапса атомов был устранен квантовой теорией. Аналогично именно квантовая теория должна привести теперь к конечной теории, взамен «бесконечных» классических пространственно-временны?х сингулярностей, возникающих при гравитационном коллапсе звезд. Но это не может быть обычная квантовая теория. Это должна быть квантовая теория самой структуры пространства и времени. Такую теорию (в случае, если она вообще появится) следовало бы назвать «квантовой гравитацией». То, что ее пока нет, не является признаком недостатка усилий, опыта или изобретательности физиков: многие первоклассные ученые с мировым именем пытались построить такую теорию, но безуспешно. Это тупик, к которому, в конце концов, пришли и мы в наших попытках понять направленность и течение времени.

Читатель может справедливо спросить: а что же, в таком случае, дало нам наше путешествие? В наших поисках понимания того, почему время кажется текущим только в одном направлении, нам пришлось побывать в начале и конце времен, там, где растворяется даже само понятие пространства. Что же мы в результате выяснили? Мы узнали, что нашим теориям пока еще недоступны ответы на эти вопросы — но что полезного это нам дает для понимания сущности разума? Я все же полагаю, что несмотря на отсутствие адекватной теории, мы можем извлечь важные уроки из нашего путешествия. А теперь нам необходимо вернуться домой. И хотя наше путешествие назад будет еще более наполнено догадками и предположениями, но других приемлемых путей назад просто нет!

Данный текст является ознакомительным фрагментом.