Ящик Хокинга: связь с гипотезой о вейлевской кривизне?

Ящик Хокинга: связь с гипотезой о вейлевской кривизне?

Как бы то ни было, а читатель вне всякого сомнения подумает: какое все это имеет отношение к ГВК или ПКТГ? Действительно, второе начало термодинамики, в его настоящем виде, вполне может быть частью процедуры R, но вот где тут в этих непрерывных «каждодневных» актах редукции вектора состояния может найтись место сколь-нибудь заметным эффектам пространственно-временны?х сингулярностей?

Чтобы прояснить этот вопрос, я хочу, хотя и с совершенно иной целью, описать здесь фантастический «мысленный эксперимент», первоначально предложенный Стивеном Хокингом.

Представьте себе герметичный ящик чудовищных размеров. Его стенки предполагаются абсолютно отражающими и непроницаемыми для любого воздействия. Сквозь них не может пройти никакой материальный объект, в том числе никакой электромагнитный сигнал, нейтрино и вообще все что угодно. Стенки отражают обратно любой объект, независимо от того, приходит ли он снаружи или изнутри, и даже действие гравитации не может проникнуть сквозь них. Такие стенки невозможно сделать ни из одного существующего в природе вещества. Никто в действительности не в состоянии выполнить описанный ниже «эксперимент». (И, как мы увидим, никто и не захочет этого делать!) Важно не это. Целью мысленного эксперимента является раскрытие общих принципов путем простого мысленного рассмотрения в принципе выполнимых опытов. Технические проблемы игнорируются при условии, что они не связаны с рассматриваемыми общими принципами. (Вспомним дискуссию о шредингеровской кошке в главе 6.) В нашем случае проблемы сооружения стенок ящика должны рассматриваться с точки зрения стоящих перед нами целей как чисто «технические», и, следовательно, ими надо пренебречь.

Внутри ящика находится большое количество вещества. Для нас не имеет значения, что это за вещество. Нас интересует только его полная масса М, которая должна быть очень большой, а также большой объем V, в который она заключена. Что же мы собираемся делать с этим дорогостоящим ящиком, а также с его совершенно неинтересным содержимым? Мы произведем самый занудный из опытов, какой только можно себе вообразить. Оставим ящик в покое — навечно!

Нас интересует окончательная судьба того, что находится внутри. Согласно второму началу термодинамики, энтропия содержимого ящика должна возрастать, пока не достигнет максимума, а вещество — состояния «теплового равновесия». После этого уже не будет происходить практически ничего интересного, если не считать «флуктуаций», приводящих к (относительно) кратковременным отклонениям от теплового равновесия. В нашей ситуации мы полагаем М достаточно большим при соответствующем V (т. е. очень большом, но не слишком большом), так что к моменту достижения «теплового равновесия» большая часть вещества сколлапсирует в черную дыру, окруженную совсем небольшим количеством вещества, и излучения, которые образуют (очень холодную!) тепловую ванну с погруженной в нее черной дырой. Чтобы быть конкретнее, примем М равной массе Солнечной системы, а V — размеру Млечного Пути! В этом случае температура «ванны» составит всего 10^-7 градуса выше абсолютного нуля!

Чтобы лучше понять природу описываемых здесь равновесия и флуюуаций, вспомним понятие фазового пространства, с которым мы познакомились в главах 5 и 7, в частности, в связи с понятием энтропии. На рис. 8.4 условно изображено все фазовое пространство Р содержимого ящика Хокинга.

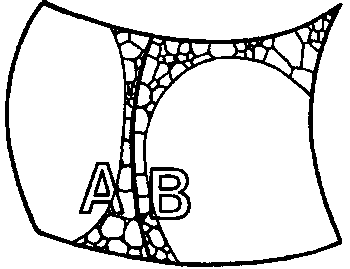
Рис. 8.4. Фазовое пространство P ящика Хокинга. Область A соответствует состояниям без черных дыр внутри ящика, а область B — состояниям, при которых внутри ящика есть хотя бы одна черная дыра

Как мы помним, фазовое пространство — это пространство с большим количеством измерений, каждая точка которого полностью отображает одно из возможных состояний рассматриваемой системы — в данном случае содержимого ящика. Таким образом, каждая точка Р содержит информацию о положениях и импульсах всех находящихся в ящике частиц, а также всю необходимую информацию о геометрии пространства-времени внутри ящика. Расположенная в правой части рис. 8.4 подобласть B (фазового пространства Р) представляет совокупность всех состояний с черной дырой внутри ящика (включая все случаи наличия более чем одной черной дыры), а расположенная слева область A представляет совокупность всех состояний без черных дыр. Представим себе дальнейшее разбиение областей A и B на меньшие ячейки для построения «грубого разбиения», необходимого для точного определения энтропии (см. рис. 7.3 гл.7 «Что такое энтропия?»). Точный вид этого разбиения нас здесь не интересует. На этом этапе нам важно лишь, что самая большая из рассматриваемых ячеек — та, что представляет состояния теплового равновесия при наличии черной дыры, — занимает большую часть области B, а (несколько меньшая) большая часть области A представляет то, что, как кажется, является тепловым равновесием, но без единой черной дыры.

Вспомним теперь, что на каждом фазовом пространстве существует поле стрелок (векторное поле), описывающих эволюцию физической системы во времени (см. главу 5, «Фазовое пространство», а также рис. 5.11). Таким образом, чтобы узнать, что произойдет с нашей системой в следующий момент, нужно просто сдвинуться вдоль стрелок (рис. 8.5).

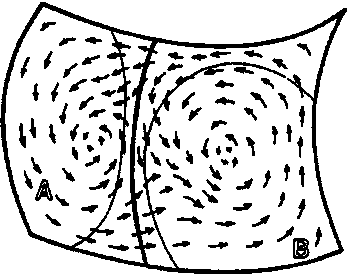
Рис. 8.5. «Гамильтонов поток» содержимого хокинговского ящика (см. рис. 5.11). Линии тока, пересекающие границу между областями в направлении от A к B, соответствуют коллапсу в черную дыру, а линии, пересекающие границу от B к A — исчезновению черной дыры в результате хокинговского испарения

Некоторые стрелки перейдут из области A в область B. Такое происходит при возникновении черной дыры в результате гравитационного коллапса вещества. А пересекают ли какие-нибудь стрелки границу между областями в обратном направлении из B в A? Такие стрелки действительно есть, но только при условии учета хокинговского испарения, о котором упоминалось ранее. В строгой классической общей теории относительности черные дыры способны только поглощать и не в состоянии ничего испускать. Но Хокингу [1975] удалось показать путем учета эффектов квантовой механики, что черные дыры все же способны — на квантовом уровне — кое-что испускать в процессе хокинговского излучения. (Это происходит в рамках квантового процесса «рождения виртуальных пар», при котором частицы и античастицы постоянно создаются из вакуума — как правило, лишь на мгновение, чтобы тут же аннигилировать, исчезнув без следа. Если есть черная дыра, она может «проглотить» одну из частиц такой пары до того, как произойдет аннигиляция, и вторая частица может покинуть черную дыру. Хокинговское излучение как раз и состоит из этих убежавших частиц.) При обычных обстоятельствах хокинговское излучение чрезвычайно слабое. Но в состоянии теплового равновесия величина энергии, теряемой черной дырой в результате хокинговского излучения, в точности компенсируется энергией, получаемой черной дырой в результате поглощения других «тепловых частиц» из окружающей «тепловой ванны», в которой дыра находится. В результате «флуктуаций» иногда может возникать небольшой избыток излучения или недостаток поглощения, что приводит к потере энергии черной дырой. Теряя энергию, черная дыра теряет также и массу (согласно формуле Эйнштейна Е=mc²) и, согласно законам, управляющим хокинговским излучением, становится чуть-чуть горячее. В очень редких случаях, если флуктуация оказывается достаточно большой, черная дыра может даже пойти в разнос, постоянно разогреваясь, теряя все больше энергии в этом процессе, непрерывно уменьшаясь в размерах, пока наконец (как мы предполагаем) совершенно не исчезнет в результате бурного взрыва! Когда это случится (и если считать, что других дыр в ящике нет), мы оказываемся в ситуации перехода из области B в область A фазового пространства Р, и значит действительно есть стрелки, идущие из области B в область A!

Я хотел бы сделать замечание о смысле, который я вкладываю здесь в понятие «флуктуация». Вспомним ячейки грубого разбиения, рассмотренные в предыдущей главе. Точки фазового пространства, принадлежащие одной ячейке, считаются (макроскопически) «неотличимыми» друг от друга. Энтропия возрастает, потому что, следуя вдоль стрелок, с течением времени мы, как правило, переходим ко все более крупным ячейкам. В конечном итоге точка фазового пространства оказывается затерянной внутри самой большой ячейки — а именно той, что соответствует тепловому равновесию (максимальной энтропии). Однако, это будет справедливо только до определенной степени. Если подождать достаточно долго, то точка фазового пространства окажется в какой-то момент в ячейке меньших размеров, и энтропия, соответственно, уменьшится. Как правило, это состояние продлится (сравнительно) недолго и энтропия вскоре снова увеличится при возвращении точки фазового пространства в самую крупную ячейку. Это — флуктуация, сопровождаемая мимолетным понижением энтропии. Обычно значительного падения энтропии не происходит, но в очень редких случаях возникает огромная флуктуация и энтропия может уменьшиться существенно и остаться малой на протяжении значительного времени.

Как раз такого рода событие и должно произойти, чтобы произошел переход из области B в область A через процесс хокинговского испарения. Очень большая флуктуация нужна потому, что маленькую ячейку необходимо протащить через то самое место, где стрелки пересекают границу между областями B и A Точно также, если наша точка фазового пространства находится внутри большой ячейки в области A (представляющей совокупность состояний теплового равновесия без черных дыр), пройдет еще очень много времени, прежде чем произойдет гравитационный коллапс и точка перейдет внутрь области B. И снова нужна большая флуктуация. (Тепловое излучения неохотно идет на гравитационный коллапс!)

Каких стрелок больше — тех, что идут из A в B; тех, что идут из B в A; или же их число стрелок обоих типов одинаково? Для нас это очень важно. Вопрос можно сформулировать иначе: что природе «проще сделать» — породить черную дыру, заставив сколлапсировать частицы в состоянии теплового равновесия или же избавиться от черной дыры через хокинговское испарение? А может оба процесса одинаково «трудные»? Строго говоря, нас интересует не число стрелок, а скорость потока объема фазового пространства. Представьте себе, что фазовое пространство заполнено некой (многомерной) несжимаемой жидкостью. Стрелки отображают поток этой жидкости. Вспомним теперь описанную в главе 5 («Неумолимое возрастание энтропии») теорему Лиувилля, гласящую, что фазовый поток сохраняет объем элемента фазового пространства — а это как раз и означает, что наша жидкость, заполняющая фазовое пространство, действительно является несжимаемой! Теорема Лиувилля как будто говорит нам, что поток из A в B должен равняться потоку из B в A, поскольку фазовая жидкость, будучи несжимаемой, не может накапливаться на одной какой-нибудь стороне. Таким образом, кажется, что черную дыру так же трудно создать из теплового излучения, как и разрушить ее!

К такому же выводу пришел и Хокинг, правда на основании несколько иных соображений. Главным аргументом Хокинга была симметричность во времени всех основных физических законов, имеющих отношение к рассматриваемой задаче (общая теория относительности, термодинамика, стандартные процедуры квантовой теории), из которой следует, что, если повернуть время вспять, то мы получим тот же самый результат, что и для прямого течения времени. Все сводится к простой смене направления всех стрелок в Р на противоположное. Из этого рассуждения действительно совершенно строго следует точное равенство числа стрелок из A в B числу стрелок из B в A при условии, что при обращении направления времени область B отображается сама на себя (а область A тоже, соответственно, отображается сама на себя). Это условие сводится к замечательной гипотезе Хокинга о том, что черные дыры и их временны?е инверсии — белые дыры — с точки зрения физики неотличимы друг от друга! Аргументация Хокинга состояла в том, что в симметричной во времени физике состояние теплового равновесия тоже должно быть симметричным во времени. Я не хочу здесь пускаться в подробное обсуждение этой поразительной возможности. Идея Хокинга состояла в том, что квантово-механическое хокинговское излучение может рассматриваться как своего рода временная инверсия классического «поглощения» вещества черной дырой. Несмотря на всю изобретательность ее автора, эта гипотеза наталкивается на серьезные теоретические трудности и я лично не верю в ее работоспособность.

В любом случае, эта гипотеза плохо согласуется с теми идеями, которые я здесь выдвигаю. Я утверждал, что несмотря на то, что черные дыры должны существовать, существование белых дыр запрещено гипотезой о вейлевской кривизне! ГВК привносит в обсуждение элемент временно?й асимметрии, не учтенный Хокингом. Следует отметить, что поскольку черные дыры и их пространственно-временны?е сингулярности действительно занимают большое место в обсуждении того, что происходит внутри ящика Хокинга, то, следовательно, рассматриваемая проблема вне всякого сомнения тоже должна быть связана с неизвестными пока физическими законами, управляющими поведением такого рода сингулярностей. Хокинг считает, что эта неизвестная физика должна иметь вид симметричной во времени квантовой теории гравитации, а я считаю — что это должна быть асимметричная во времени ПКТГ! Я утверждаю, что одним из главных следствий ПКТГ должна быть ГВК (и, следовательно, второе начало термодинамики в известном нам виде), и поэтому необходимо попытаться установить, какие из ГВК вытекают следствия для рассматриваемой проблемы.

Посмотрим, как включение ГВК отразится на обсуждении потока «несжимаемой жидкости» в фазовом пространстве Р. Действие чернодырной сингулярности в пространстве-времени состоит в том, что она поглощает и разрушает все попадающее на нее вещество. Для нас же гораздо важнее, что эта сингулярность уничтожает информацию! Следствием этого для фазового пространства P является слияние некоторых линий тока (рис. 8.6).

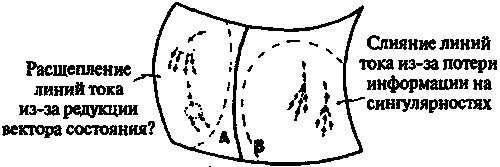
Рис. 8.6. В области B должно происходить слияние линий тока из-за потери информации на сингулярностях черных дыр. Компенсируется ли слияние порождением новых линий тока в результате R-процедуры (главным образом в области A)?

Два состояния до этого различные могут превратиться в одно, как только различающая их информация окажется уничтоженной. При слиянии линий тока в фазовом пространстве Р мы фактически имеем дело с нарушением теоремы Лиувилля. Наша жидкость больше не является несжимаемой, а непрерывно уничтожается в области B!

Похоже, что теперь мы оказались в действительно трудном положении. Если «жидкость» постоянно уничтожается в области B, то число линий тока из А в B должно превышать число линий тока из B в A, откуда следует, что породить новую черную дыру легче, чем уничтожить уже имеющуюся! Все это действительно имело бы смысл, если бы не то обстоятельство, что теперь количество «жидкости», покидающее область A, превышает количество «жидкости», которое возвращается в эту область. Черных дыр в области A нет, а существование белых дыр исключается ГВК — и поэтому теорема Лиувилля должна вне всякого сомнения абсолютно точно выполняться в области A! Однако теперь, похоже, нам нужно каким-то образом «порождать жидкость» в области A для восполнения ее потери в области B. Какой механизм может обеспечить увеличение числа линий тока? По-видимому, нам потребуется, чтобы в некоторых случаях одно и то же состояние могло приводить к более чем одному результату (т. е. допустить возможность бифуркации линий тока). Такого рода неопределенность эволюции физической системы в будущем «попахивает» квантовой теорией — ее R-частью. Возможно ли, чтобы R была в некотором смысле «оборотной стороной монеты» к ГВК? В то время, как ГВК обеспечивает слияние линий тока в области B, квантово-механическая R-процедура приводит к бифуркациям линий тока. Я действительно утверждаю, что именно объективный квантово-механический процесс R редукции вектора состояния приводит к бифуркациям линий тока и таким образом в точности компенсирует их слияние, вызываемое ГВК (см. рис. 8.6)!

Для того, чтобы такое расщепление произошло, R-процедура должна быть, как мы уже видели, асимметричной во времени: вспомним описанный выше эксперимент с лампой, фотоэлементом и полупосеребренным зеркалом. В случае излучения лампой фотона возможны два (одинаково вероятных) результата этого процесса: либо фотон попадает на фотоэлемент и последний регистрирует его, либо фотон попадает на стену в точке А и фотоэлемент не срабатывает. В фазовом пространстве этого эксперимента мы имеем линию тока, представляющую излучение фотона, и эта линия тока расщепляется на две: одна часть представляет ситуацию, когда фотоэлемент срабатывает, а другая — когда он не срабатывает. Здесь мы, по-видимому, имеем дело с самой настоящей бифуркацией: одно допустимое состояние на входе и два возможных состояния на выходе. Второе входное состояние, которое следовало бы рассмотреть, — это испускание фотона из точки В на лабораторной стене, и в этом случае мы имели бы два состояния на входе и два на выходе. Однако только что упомянутое альтернативное состояние на входе исключается по причине его противоречия со вторым началом термодинамики — т. е. исходя из изложенной здесь концепции, и, в конечном итоге, по причине противоречия с ГВК при отслеживании эволюции системы назад в прошлое.

Я должен еще раз отметить, что излагаемая мною здесь точка зрения на самом деле не является «традиционной» — хотя мне и не совсем понятно, как «традиционные» физики предлагают решать все поставленные здесь проблемы. (Я подозреваю, что немногие из них вообще серьезно над ними задумывались!) Разумеется, я слышал разные точки зрения. Например, время от времени некоторые физики выдвигали предположение о том, что хокинговское излучение никогда не приводит к полному исчезновению черной дыры, и что от нее всегда остается своего рода «ядрышко». (И, следовательно, согласно этой точке зрения стрелок из B в A нет!) На самом деле это почти никак не скажется на мои рассуждениях (и фактически даже усилит их). Можно, однако, избежать моих выводов, если постулировать, что общий объем фазового пространства Р на самом деле бесконечен, но это противоречило бы некоторым весьма фундаментальным представлениям об энтропии черных дыр и природе фазового пространства замкнутых (квантовых) систем, а другие технические приемы, позволяющие избежать моих выводов, о которых мне доводилось слышать, представляются еще менее удовлетворительными. Гораздо более серьезное возражение состоит в том, что построение ящика Хокинга требует слишком сильной идеализации, и что, предполагая возможность его создания, мы вынуждены преступать некоторые барьеры принципиального характера. Хотя я сам не до конца в этом уверен, но все же склоняюсь к тому, чтобы считать некоторую необходимую идеализацию вполне допустимой!

Наконец, есть один серьезный аспект, о котором я умолчал. Я начал обсуждение, предположив, что мы имеем дело с классическим фазовым пространством — а теорема Лиувилля относится к классической физике. Но затем пришлось рассмотреть квантово-механический феномен хокинговского излучения. (Кроме того, квантовая теория нужна для обеспечения конечной размерности и конечного объема Р.) Как мы видели в главе 6, квантовым аналогом фазового пространства является гильбертово пространство, и, поэтому, следовало бы, наверно, проводить все наши рассуждения в терминах гильбертова, а не фазового пространства. Для гильбертова пространства существует аналог теоремы Лиувилля, который следует из так называемого «унитарного» характера временно?й эволюции U. Не исключено, что все мои рассуждения можно сформулировать полностью в терминах гильбертового, а не классического фазового пространства, но мне трудно представить себе, каким образом в этом случае можно рассматривать классические явления, связанные с пространственно-временно?й геометрией черных дыр. Я считаю, что для правильной теории непригодно ни классическое фазовое пространство, ни гильбертово пространство, а потребуется какой-то новый, до сих пор еще не открытый тип математических пространств, занимающий промежуточное положение между двумя упомянутыми выше. Соответственно, мои рассуждения следует рассматривать только в эвристическом смысле, и они представляют собой скорее всего лишь общие предположения, а не окончательные выводы. Тем не менее, я действительно считаю свои рассуждения сильным доводом в пользу глубинной связи между ГВК и R, откуда вытекает, что R-процедура действительно должна представлять собой эффект квантовой теории гравитации.

Повторю свои выводы еще раз: я выдвигаю гипотезу, согласно которой квантовомеханическая редукция вектора состояния действительно является оборотной стороной ГВК. В соответствии с этой гипотезой два важнейших следствия нашей искомой правильной квантовой теории гравитации (ПКТГ) — это ГВК и процедура R. ГВК приводит к слиянию линий тока в фазовом пространстве, в то время как процедура R приводит к расщеплению линий тока, в точности компенсирующему их слияние, вызванное ГВК. Оба процесса теснейшим образом связаны со вторым началом термодинамики.

Отметим, что слияние линий тока происходит только в области B, в то время как их расщепление может иметь место как внутри области A, также и внутри области B.

Вспомним, что A представляет совокупность состояний, в которых черные дыры отсутствуют, и, следовательно, редукция вектора-состояния действительно возможна при отсутствии черных дыр. Ясно, что для выполнения R совсем необязательно иметь в лаборатории черную дыру (как в случае только что рассмотренного нами эксперимента с фотоном). Нас сейчас интересует лишь общий баланс между различными возможными событиями в той или иной ситуации. В рамках излагаемой концепции отсутствие детерминизма в квантовой теории должно всего лишь компенсироваться возможностью образования черных дыр на некотором этапе (и следующей отсюда возможностью уничтожения информации)!

Данный текст является ознакомительным фрагментом.