ГЛАВА 6 Еще о трамплинах…
Какие трамплины были или могли быть у Д. Менделеева при открытии периодического закона? Прежде чем перейти к области технических изобретений, рассмотрим несколько примеров трамплина в творчестве химиков. Вернемся к открытию периодического закона Д. Менделеевым. В чем именно состоял тогда основной ППБ — мы уже видели. Мы знаем также первые записи, сделанные рукой ученого на обороте присланного ему письма, которыми началось преодоление барьера, стоявшего на пути к истине. Но в чем конкретно заключался трамплин, подсказавший Дмитрию Ивановичу мысль о сближении химически несходных элементов по величине их атомных весов, мы не знаем. Можно только гадать об этом и высказывать гипотезы. Так как первая запись была «КС1», го вполне возможно, что знаменитый химик сделал ее как случайную, продиктованную тем, что первая часть «Основ химии» завершалась хлором (С1) и его аналогами, а вторая их часть, над которой он как раз и работал в тот момент, открылась калием (К) и его аналогами. В пользу такого предположения говорит свидетельство самого ученого, что «главное — периодичность элементов, найденная именно при обработке «Основ химии».
И тем не менее нельзя точно установить, как у него сработал трамплин в тот самый начальный момент. Но это можно сделать с большой достоверностью в отношении другого, гораздо менее значительного трамплина, проявившего себя в тот же день немного позднее.
Отметим, что Д. Менделеев любил во время отдыха от научных занятий раскладывать пасьянс. И вот, когда уже был найден ключ к открытию периодического закона, то есть преодолен барьер на пути к открытию, Д. Менделеев стал записывать расположение элементов в виде таблицы.
Однако далеко не сразу и отнюдь не для всех элементов находилось правильно место в строящейся системе. Элементы и даже целые их группы приходилось постоянно переставлять с места на место, а это требовало все нового и нового переписывания всей строящейся таблицы. А так как общее число элементов было достаточно большим (64), то доведение открытия до конца явно затягивалось надолго. В этот момент Дмитрия Ивановича навестил А. Иностранцев. Полвека спустя (в 1919 году) он вспоминал, что застал ученого стоящим у своей рабочей конторки в расстроенном состоянии. Д. Менделеев признался ему, что в отношении систематики элементов у него в голове все уже сложилось, а выразить таблицей (то есть записать на бумаге) он не может.
Когда А. Иностранцев ушел, произошло, если судить по последующим действиям Д. Менделеева, главное: он преодолел стоявший перед ним ППБ, согласно которому таблицу надо составлять, обязательно записывая ее сразу на бумаге, и понял, что необходим новый способ записи. Потом, уже в наше время, академик А. Ферсман назовет его раскладыванием «химического пасьянса». Сам жа Д. Менделеев в «Основах химии» запишет: «Вот я и стал подбирать, написав на отдельных карточках элементы, с их атомными весами и коренными свойствами, сходные элементы и близкие атомные веса, что быстро и привело к тому заключению, что свойства элементов стоят в периодической зависимости от их атомного веса…»
Здесь ничего еще не сказано о трамплине, который подсказал выдающемуся химику путь преодоления ППБ, переходя от написания таблицы на бумаге к раскладыванию пасьянса. Может быть, стоя в растерянности у конторки, Д. Менделеев увидел колоду игральных карт или же только вспомнил о ней, а может быть, ему на глаза попались лежавшие у него на конторке визитные карточки. Это неизвестно.
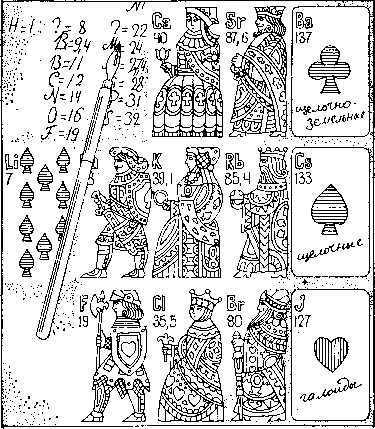
Но, вероятнее всего, трамплином оказался уже набросанный на бумаге первый незаконченный вариант таблицы. Присмотримся к его верхней части. Вот он:
Са=40 Mg=87,6 Ва=137 (щелочноземельные)
Li=7 Na=23 K=39,l Rb=85,4 Сz=133(щел. металлы)
F=19 01=35,5 Br=80 J=127 (галоиды).
Здесь ясно выступило (еще до раскладывания пасьянса), что элементы распределяются в горизонтальные ряды как бы «по масти» (например, щелочные металлы или галоиды), а в вертикальные столбы — «по значению», то есть по близости атомных весов (например, 40; 39,1; 35,5).
Любитель карточных пасьянсов, каким был Д. Менделеев, не мог не заметить удивительного сходства с расположением игральных карт в некоторых пасьянсах. Ведь для того, чтобы пасьянс получился, карты в нем должны располагаться в определенной зависимости от масти и значения.
Такое поразительное сходство не могло бы остаться незамеченным для ученого, наделенного ассоциативным мышлением, и, следовательно, не могло бы рано или поздно не выступить в ходе его научного творчества как трамплин, указавший путь к преодолению ППБ.
Добавим, что весь ход химического пасьянса ученый зафиксировал на бумаге, и это нами было дешифровано в 1949 году. Какие при этом возникали перед нами своеобразные барьеры и с помощью каких трамплинов они были преодолены, рассказано ниже.
Реконструкция менделеевского химического пасьянса. Прежде всего барьером (ППБ) при попытке реконструировать ход химического пасьянса, который был разложен Д. Менделеевым 17 февраля (1 марта) 1869 года, явилось само истекшее с того момента время. Казалось бы, никакие записи, сделанные Дмитрием Ивановичем, дошедшие до нас, не могли помочь нам установить, в какой последовательности раскладывались и переставлялись с места на место карточки с элементами. Задача решалась последовательными этапами, и ключ к выяснению очередного этапа ее решения находился каждый раз при тщательном анализе менделеевских записей. Я не могу здесь подробно разобрать каждый наш шаг (мы работали вместе с моей покойной женой Т. Н. Ченцовой), но отмечу лишь некоторые моменты.
В первую очередь надо было выяснить, с чего и как началось «раскладывание пасьянса». Легко было установить, что первыми заняли свои места, естественно, наиболее изученные элементы, начиная со щелочных металлов и следующих за ними галогенов (галоидов), в течение всего дальнейшего пасьянса они ни разу не меняли своих мест. Таких элементов оказалось 27, то есть немногим меньше половины всех вообще известных тогда элементов.
За ними следовали менее изученные, которые были выписаны на полях вне самой таблицы, на ее рижнем и верхнем краях и в других местах. Так, внизу таблицы было записано в случайном порядке 17 элементов, которые затем вычеркивались. Невычеркнутым остался один индий.
Легко было догадаться, что остальные 16 последовательно вычеркивались из подготовительного списка каждый раз, когда карточка соответствующего элемента включалась в пасьянс. В итоге в конце этого этапа в таблицу были вписаны еще 30 элементов, то есть всего уже 57.
Значит, к этому времени вне пасьянса оставалось только 7 карточек. Их Д. Менделеев записал в правом верхнем углу своей таблицы, и из него он вычеркнул три элемента: два он включил в пасьянс, а третий (тербий) обвел овальной рамкой и под ним подписал: «несу по б». Это был первый менделеевский ребус, который заставил нас поломать голову.
Что может означать это «несу»? Жена как-то спросила: «А не записан ли где-нибудь тербий в самой таблице?» Я ответил, что его там нигде нет. «А почему? Не объясняется ли это тем, что у Менделеева было основание считать, что тербия вообще не существует?» — спросила она.
Ее вопрос явился подсказкой: «несу» — значит не существует, догадался я тут же. А три следующие буквы «по б» должны означать, по мнению какого ученого тербия вообще нет в природе. Я бросился к первому изданию «Основ химии», к тем главам их второй части, которые писались после открытия периодического закона. И там я нашел ответ: по мнению Бунзена и Бара, тербия вообще не существует. Так был решен этот ребус.
Значит, общее число карточек оказалось на одну меньше, а именно 63. Из них теперь в пасьянс вошло 60.
Второй ребус, заданный нам Д. Менделеевым, оказался сложнее. Над нижним списком элементов, размещаемых в таблице, было записано: «невзо In, Er, Th, It».
Причем три последних записано общим росчерком. Что это могло значить?
Мы решили сначала, что недописанное слово означает имя какого-то химика. Если русского, то Невзорова, если иностранца — то, скажем, Хебсона (Hebson).
Но химиков с такими именами обнаружить не удалось. Покойный Г. Быков прочитал «невзо» как немного искаженное немецкое слово «Uber» (вверху или наверх). Он объяснил это тем, что упомянутые здесь четыре элемента попали у Дмитрия Ивановича на самый верх его окончательной таблицы. Но это нам показалось натяжкой, и ребус очень долго оставался нерешенным.
Наконец, причудливым образом пришла подсказка. Как-то раз мы с женой были на «Прекрасной Елене», и когда Менелай начал вопрошать: «Взошел ли Парис на ложе Елены или не взошел?» — мы оба внезапно догадались, что недописанное «невзо» означает «не взошли». Ведь Д. Менделеев частицу отрицания часто не отделял от основного слова, а это последнее сокращал на гласной букве. Значит, мучившая нас запись означала, что к концу пасьянса в него не были включены последние четыре карточки, причем три из них (зачеркнутые) были затем включены, а самой последней оставалась карточка индия.
Теперь оставался неразгаданным третий менделеевский ребус: на верхнем краю таблицы значилось: «надо (одно слово неразборчиво) Са Ва Sr».
Было непонятно, что «надо»? Я написал в Ленинград М. Менделеевой-Кузьминой, дочери ученого, и ее помощнику Р. Добротину, прося их помочь разгадать неразборчивое слово. При этом я рассказал о проделанной нами работе по реконструкции химического пасьянса и о том, что я установил следующее: в момент раскладывания этого пасьянса Дмитрий Иванович закончил написание первых двух глав второй части «Основ химии» — о щелочных металлах — и готовился приступить или уже приступил к написанию следующей, третьей, главы о теплоемкости.
В очередной свой приезд в Ленинград я услышал от Р. Добротина, что он разгадал интересовавшее меня слово: «надо теплоем[кость] Са Ва Sr». «Мне, — добавил он, — разгадку подсказало Ваше письмо, где Вы сообщили, что Д. Менделеев ко времени пасьянса занимался главой о теплоемкости».
Услышав это, я сам прочел названную главу в «Основах химии», и там значилось следующее: для того, чтобы убедиться в истинности атомных весов щелочноземельных металлов, надо определить теплоемкость кальция, бария, стронция. Не понимаю, как я мог раньше не обратить внимания на эту фразу! Ведь здесь и порядок перечисления — Са, Ва, Sr — был такой же, как наверху «пасьянсной» таблицы. По-видимому, мне не хватило тогда ассоциативного мышления, которое, к счастью, проявил Р. Добротин.
Последняя менделеевская загадка была особенно интересной. А. Иностранцев в 1919 году вспоминал, что Сказал ему Д. Менделеев после первой публикации, содержавшей сообщение о сделанном открытии. Ученый будто бы говорил, что долгое время у него ничего не получалось с таблицей элементов; усталый, он прилег и заснул. Во сне увидел таблицу, в которой элементы были расставлены «как надо». Встал и записал ее на бумаге. Впоследствии только в одном месте потребовалось исправление.
Так вспоминал А. Иностранцев. Но прошло целых полвека, и его память могла его подвести. А мы занялись этим вопросом еще 30 лет спустя, когда живых свидетелей происходившего в квартире Д. Менделеева в день открытия периодического закона не осталось. Можно ли было при таких условиях проверить правильность рассказа А. Иностранцева? Стоявший перед нами барьер, созданный протекшим временем был велик. Тем более что задача состояла в выяснении того, что мог увидеть ученый во сне после своего химического пасьянса.
М. Менделеева-Кузьмина дала мне на просмотр все сохранившиеся у нее в музее-архиве рукописные таблицы ее отца. И вот одна из них в точности соответствовала тому, что рассказывал А. Иностранцев: в ней элементы были расставлены «как надо», то есть не в порядке убывания атомных весов, а в порядке их возрастания, во-первых. А во-вторых, при ее публикации действительно только в одном месте Д. Менделеев сделал исправление, вычеркнув ошибочно предсказанные им два элемента («?=8;?=22») между водородом и медью.
После появления рассказа А. Иностранцева распространилась версия, будто Д. Менделеев сделал свое открытие во сне. Эта нелепость была теперь полностью опровергнута, поскольку во сне Дмитрий Иванович только «переписал» свою законченную таблицу в обратном порядке.
Таковы были познавательно-психологические ребусы и задачи, связанные с менделеевским химическим пасьянсом.
Трамплин при изобретении противогаза Н. Д. Зелинским. Вскоре после начала империалистической войны 1914–1918 годов, то есть первой мировой войны, кайзеровская Германия применила химическое оружие. На западном фронте, у реки Ипр, на французские и английские окопы немцы выпустили впервые огромное облако удушливого газа — хлора. Это случилось в конце апреля 1915 года. Спустя месяц такой же газовой атаке были подвергнуты русские войска на восточном фронте. В качестве защиты от газа стали использоваться марлевые маски, пропитанные водным раствором гипосульфита натрия (восстановитель!) и соды. Такой «мокрый противогаз» химически реагировал с хлором, удаляя его из воздуха.
Тогда был применен новый удушливый и вместе с тем отравляющий газ (хлорпикрин), который пробивал существовавшие тогда противогазы, так как не реагировал химически с гипосульфитом и содой. Но он химически связывался с другим веществом (уротропином), что привело к созданию нового химического противогаза.
Однако у противника всегда оставалась возможность прибегнуть к какому-нибудь третьему удушающему или отравляющему газу, который пробивал все известные химические противогазы, так что задача организации простой химической защиты оставалась бы все равно нерешенной.
Обратим внимание на то, что первоначальные средства защиты от газов основывались на учете специфических химических, то есть особенных, свойств газов и их поглотителей. Можно сказать так, что все дело химической защиты стояло вначале на ступени особенности. Это обстоятельство способствовало выработке некоторого ППБ, заключавшегося в том, что средства защиты от газов надо искать в химии, в использовании химических свойств веществ. Между тем все настойчивее вставала задача создания универсального противогаза, способного улавливать и удалять из воздуха все опасные для человека газы вообще — как ныне уже применяемые, так и газы, изобретение которых возможно в будущем. Такую задачу и решил в том же 1915 году Н. Зелинский.
Чтобы понять, в чем состояла сущность его изобретения, вспомним то, как был открыт периодический закон Д. Менделеевым: тогда совершился переход со ступени особенности, в рамках которой изучалась до тех пор элементы лишь по их химическому сходству, на ступень всеобщности, представленной общефизическим свойством массы (атомного веса), по которому можно было сближать несходные элементы между собой. Значит, особенное здесь было представлено химией, а всеобщее — физикой (см. главу 1). Затем точно такое же соотношение категорий особенного и всеобщего мы видели в главе 3, когда говорили о переходе от химического (препаративного) анализа к физическому (спектральному и физикохимическому).
Аналогичную картину мы видим и в истории создания Н. Зелинским своего универсального (сухого угольного) противогаза. Создать такой противогаз означало выйти за рамки изобретения все новых и новых химических средств защиты от газов (особенного) и подняться на уровень всеобщего, когда решается задача улавливания всех опасных для человека газов вообще.
Каким же образом Н. Зелинскому удалось преодолеть в данном случае ППБ, другими словами, что именно послужило ему подсказкой (трамплином) в решении этой исключительно важной задачи, в результате чего была спасена жизнь многим тысячам людей?
Автору этих строк посчастливилось в бытность свою студентом химфака 1-го МГУ слышать из уст самого Н. Зелинского рассказ о том, как был им изобретен противогаз.
После ухода (в 1911 году) из Московского университета в знак протеста против царского произвола Н. Зелинский переехал в Питер, где стал заведовать Центральной лабораторией министерства финансов. Лаборатория эта обслуживала предприятия спирто-водочной промышленности. Одной из применявшихся там операций была очистка спирто-водочных изделий от всякого рода механических примесей и взвесей при помощи активированного (древесного) угля. Очевидно, что действие древесного угля (адсорбция им других тел) носило чисто физический, но не химический характер.
Когда пришли сводки о первой (майской) газовой атаке, то выяснилось, что русские войска использовали как защиту от газов такие доморощенные средства, как завертывание головы в шинель, как дыхание через разрыхленную землю и т. п., что давало хороший эффект. Очевидно, что и здесь действовал физический фактор (адсорбция), но не химический; то есть всеобщее (по отношению к любому газу), а не особенное (по отношению только к одному данному).
Обладая в высокой степени способностью к наблюдению и ассоциативному мышлению, Н. Зелинский сумел связать два факта: сообщение о том, каким путем спасались от удушения газами люди на фронте, и каково действие древесного угля при очистке спирта. И там и тут выступал как всеобщее один и тот же физический фактор — адсорбция.
Именно сообщения с фронта о майской химической атаке и ее результатах явились трамплином для научно-изобретательской мысли Н. Зелинского, которая уже в июне 1915 года преодолела возникший тогда ППБ в деле противохимической защиты.
Вот как свидетельствовал об этом сам изобретатель: «В официальных сообщениях с фронта подробно описывалась обстановка газовых атак, случаи поражения от них и немногочисленные случаи спасения… Сообщалось, что только те оставались в живых, кто прибегал к таким простым средствам… как дыхание через рыхлую землю, плотно касаясь ее ртом и носом, или, наконец, спасались те, кто покрывал голову шинелью и спокойно лежал во время газовой атаки…
Последнее обстоятельство произвело на нас большое впечатление и, обсуждая затем вопрос о возможных мерах борьбы с газовыми атаками, мы решили испробовать и применить такое простое средство, действие которого было бы вполне аналогично действию материи шинели или гумусу почвы. Как в том, так и в другом случае ядовитые вещества связывались не химически, а поглощались, или адсорбировались, шерстью и почвой.
Такое средство мы думали найти в древесном угле».
Так сработал трамплин при осуществлении одного из самых замечательных и удивительно гуманных химических изобретений. Когда в 1929 году во время «чистки профессуры» Н. Зелинский отчитывался перед народом за свою научную деятельность, он с гордостью сказал, что, по сути дела, он вступил в социалистическое соревнование еще в 1915 году, изобретя угольный противогаз, который спас столько человеческих жизней. Зал клуба Дорогмиловского химзавода, где выступал Н. Зелинский, ответил бурными признательными аплодисментами на эти слова старого ученого.
Не могу не упомянуть в связи со сказанным еще об одном эпизоде. Вскоре после окончания Великой Отечественной войны я написал для журнала «Пропагандист Красной Армии» статью об изобретении Н. Зелинским противогаза. В ней я провел методологическую параллель между открытием периодического закона Д. Менделеевым и изобретением угольного противогаза Н. Зелинским. Ведь и там и тут совершился однотипный переход с химической ступени особенности на физическую ступень всеобщности.
Редакция журнала предварительно послала рукопись моей статьи на отзыв самому Н. Зелинскому, и вскоре от него был получен не просто одобрительный, а буквально восторженный отзыв. Из скромности он добавил только, что не считает свое столь рядовое, по его словам, открытие удобным ставить на одну доску с таким великим открытием всемирного значения, как менделеевское.
Я, как автор, безмерно счастлив, что сумел довести до сведения творца универсального противогаза оценку его изобретения как совершившегося в порядке восхождения от особенного ко всеобщему и получить его одобрение.
ППБ в парадоксе Гиббса и трамплин при его преодолении. В заключение этой главы позволю себе привести случай из личного опыта. В 1927 году мой университетский учитель, профессор А. Раковский читал курс по химической термодинамике; в одной из лекций он рассказал о так называемом парадоксе Гиббса, который состоял в следующем: когда смешиваются два различных химически не взаимодействующих газа, их энтропия S возрастает на одну и ту же. величину ?S. Но если смешиваются такие же количества одного и того же газа, то их энтропия остается без изменения, то есть ?S=0. Мы можем взять сколько угодно знало различающихся газов и уменьшить до предела их различия, и все же ?S при их смешении всегда будет иметь место, иначе говоря, их S будет возрастать на одну и ту же величину. Важно, чтобы оба газа хоть в чем-нибудь различались между собой. Но если в пределе они станут тождественными, то есть превратятся в две части одинакового газа, ?S немедленно скачком обратится в нуль.
Дж. Гиббс, увидевший этот парадокс, не мог его объяснить сам. Дело в том, что энтропия S есть чисто математическая величина и непосредственно не измерима физически. Для ее определения необходимо измерить работу, совершенную при данном физическом процессе (скажем, при смешении газов), а затем полученное ее значение разделить на абсолютную температуру. Поэтому ученые, пытавшиеся решить парадокс Дж. Гиббса, стали искать способы определения работы при смешении (взаимной диффузии) двух различных газов, так как только в таком случае можно было вычислить ?S для подобных процессов. При смешении же двух частей одного и того же газа (его автодиффузии) заранее было известно, что никакой работы при этом не может совершаться и что поэтому-то энтропия останется без изменения (?S=0).
Над этим парадоксом тщетно бились многие выдающиеся физики, такие, как В. Нернст, И. Ван дер Ваальс, Г. Лоренц, М. Планк, Э. Шредингер, П. Дюгем и многие другие. Были предложены различные частные решения, однако общего решения все же не было найдено.
Так нам, студентам, рассказывал А. Раковский. И он разобрал два типичных частных случая решения парадокса Гиббса. Оба они состояли в придумывании мысленного кругового процесса, результатом которого было бы получение, тоже, конечно, мысленное, определенной работы. Отсюда для разных газов выводилось бы значение ?S (возрастание энтропии), а для частей. одного и того же газа — отсутствие ее возрастания (?S=0). При этом каждый из обоих способов основывался на учете каких-то специфических свойств смешиваемых газов.
Так, один круговой процесс строился на применении мифических «полупроницаемых перегородок». Представим себе, что внутри цилиндра имеются два поршня-перегородки, двигающиеся в противоположных направлениях (см. рис. 1).
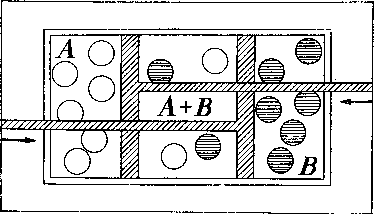
Рис. 1
Поршень левый проницаем для газа А, но не проницаем для газа В, а поршень правый, наоборот, пропускает только один газ В и не пропускает газ А. Тогда работа смешения обоих газов (А и В) будет равна работе расширения обоих газов вдвое, если они до смешения занимали равные объемы при одинаковой температуре. Отсюда легко получается значение ?S. Но очевидно, что подобных «полупроницаемых перегородок» в принципе нельзя придумать для двух частей одного и того же газа. Для большей убедительности назывались конкретные газы и соответствующие им перегородки. Скажем, А — это водород, а В — аммиак. В таком случае левая перегородка будет нагретая платиновая пластинка (она пропускает водород и не пропускает аммиак), а правая перегородка — водяная пленка, пропускающая аммиак, но не водород.
Искусственность и явная неполнота решения тут налицо; ведь в таком случае два изотопа одного и то же элемента, например хлора, а тем более неона, будут вести себя как части одинакового газа, то есть давать ?S=0, хотя они, несомненно, различаются между собой, а потому должны при смешении давать обычное ?S.
Другое решение — не менее искусственное и причудливое. Оно основано на различии газов по массе их частицы (молекулярном весе). Представим в поле земного тяготения бесконечно высокий столб газов. В нижней его части собрался один лишь тяжелый газ, в верхней — один легкий, а в середине — смесь обоих газов. Мы можем теперь мысленно представить, что по краям столба сверху и снизу вводятся равные количества обоих газов, а из середки столба извлекаются те же количества, причем совершается работа, как раз соответствующая ?S при смешении разных газов. Когда же массы частиц газов одинаковы, примыслить подобного столба, конечно, нельзя. В итоге якобы решается парадокс Гиббса.
Но ведь у газообразных изобаров тоже получится ?S=0. Значит, и в этом случае нельзя с помощью придуманного кругового процесса четко отделить все различные газы, ведущие себя при смешении одинаковым образом (дающие ?S во всех случаях, независимо от характера и степени их различия), от частей одного и того же любого газа, дающих при автодиффузии ?S=0.
Так рассказывал А. Раковский. Со своей стороны он высказал предположение, что причина парадокса кроется в обезличении идеальных газов, то есть в игнорировании индивидуальных членов А и В, которые (по Ван дер Ваальсу) должны входить в уравнение состояния реальных газов.
Мы умышленно привели так подробно изложение А. Раковским сущности парадокса Гиббса и историю попыток его решения многими выдающимися учеными. Нам хотелось показать, какой усложненно запутанной была вся эта проблехма к концу 20-х годов нашего века и как было рискованно еще не закончившему университетский курс студенту браться за ее решение. Но я все-таки взялся и настолько увлекся ею, что ходил как отрешенный, перестал спать, вовремя есть и пить, так что товарищи-сокурсники шептались о том, не заболел ли я психически? Опасения их, казалось бы, имели основания: возня со всякими там «полупроницаемыми перегородками» да «бесконечными столбами» для нормального рассудка не сулила ничего хорошего. Расскажу о ходе моей мысли.
Было ясно, что не следует придумывать каких-то новых круговых процессов и вообще связывать решение парадокса с индивидуальными свойствами различных газов. Ведь с самого начала было известно, что ?S при смешении любых газов равна (при одинаковых условиях) одной и той же величине, независимо от природы самих газов и степени их различия. Значит, не в их химических свойствах и не в массе их частицы надо было искать разгадку.
Теперь, так сказать задним числом, я бы сказал, что методологически вопрос здесь стоял так, как в случае с изобретением противогазов и других разобранных выше принципиально аналогичных случаях. Ступень особенности была уже исчерпана, и предстояло преодолеть ППБ, стоявший на пути ко всеобщему. Я тогда об этом не догадывался и только теперь могу сделать такой вывод.
Моя мысль работала так: я увлекался тогда книгой В. И. Ленина «Материализм и эмпириокритицизм», особенно ее пятой главой и вообще ленинской критикой «физического» идеализма. На меня особенно сильное впечатление произвел ленинский анализ кризиса физики и его резюме: «Материя исчезает», остаются одни уравнения». «Вот бы мне найти случай подобного исчезновения материи, — часто думал я, — и попытаться восстановить ее в ее правах!» Парадокс Гиббса мне и показался сразу же весьма подходящим случаем. Но как его решить?
Я занялся штудированием всей известной литературы на всех европейских языках, включая голландский. Из основного труда Гиббса, переведенного на немецкий язык В. Оствальдом, я подробно выяснил, как и откуда возник парадокс, а из других источников — как он решался до сих пор. Я установил, что при выведении формулы для энтропии S газовой смеси Дж. Гиббс воспользовался законом Дальтона, выражающим аддитивность парциальных давлений разных газов в их смеси, то есть независимость между собой. Однако никакого вывода отсюда я поначалу еще не сумел сделать. Главным препятствием казалась неясность того, как ведут себя смешиваемые газы по отношению друг к другу при их взаимной диффузии.
Как-то в начале осени я наблюдал падающие с деревьев листья. Они походили на большие частицы газов, которые смешивались между собой. Однако такой образ ничего мне не говорил, и я тщетно ломал голову над ответом на вопрос: как же ведут себя по отношению друг к другу разные газы во время диффузии? Задумавшись, я не заметил, как ко мне пбдсел мой сокурсник-химик, которого я не видел после летних каникул. Он что-то горячо говорил мне, но я даже не замечал его, думая о своем. Тогда мой собеседник сердито воскликнул: «Да ты не слушаешь меня! Я битый час говорю тут как в пустоту!» И тут до моего сознания дошли его последние слова: «Как в пустоту».
Это была долгожданная подсказка (трамплин, как я сказал бы сейчас): разные газы, смешиваясь, ведут себя как пустота по отношению друг к другу, а одинаковые — нет, и в этом ключ к решению так долго мучившей меня, да и не только меня, загадки! Схватив товарища за руку и боясь, что ослышался, я закричал на весь садик: «Что ты сказал? Что ты сказал? Повтори еще раз!» Он с удивлением и даже, как мне показалось, с некоторым испугом посмотрел на меня, вспомнив, вероятно, разговоры о моей психике. Ну а я помчался в лабораторию и принялся лихорадочно делать выкладки и записи.
Все сразу же стало на свои места. Если разные газы ведут себя по отношению друг к другу как пустота, то это значит только, что они в их смеси подчиняются одному общему физическому закону — закону Дальтона, гласящему, что давление смеси равно сумме давлений отдельных газов в этой смеси. Поэтому-то при образовании их смесн их суммарная энтропия и возрастает на величину ?S.
Но закон Дальтона и его действие совершенно не зависит от природы самих смешанных газов (лишь бы они химически не взаимодействовали между собой) и от степени их различия. Следовательно, этот закон отличается точно такими же чертами, как сама парадоксальная величина ?S. Когда же мы имеем дело с частями одного и того же газа, то закон Дальтона для них исчезает полностью и они ведут себя друг по отношению к другу не как пустота, а, напротив, как непроницаемое пространство.
Парадокс был решен, причем его решение носило не частный характер, касающийся лишь некоторых особенных газов, но всех газов вообще. Другими словами, удалось в данном случае осуществить переход со ступени особенности на ступень всеобщности.
Я, разумеется, тут же обнаружил, что ключ к решению своего парадокса дал сам же Дж. Гиббс, когда он положил закон Дальтона в основу вывода формулы для энтропии газовой смеси. Отсюда следовало непосредственно, что для газовых систем, где закон Дальтона не действует, не имеет места и возрастание энтропии ?S. Но ни мне, ни кому-либо другому такая простая мыель, с порога. устранявшая парадокс, почему-то не пришла в голову.
Вскоре в Большой химической аудитории на открытом заседании кафедры А. Раковского под его председательством я сделал доклад о предлагаемом мною решении парадокса Гиббса. Я говорил о том, что хотел вернуть на свое место якобы «исчезнувшую материю» с тем, чтобы оставшиеся математические уравнения получили физически вещественное обоснование, и это удалось сделать, связав математическую величину (энтропию) с совершенно точным физическим, материальным отношением (законом Дальтона).
А. Раковский, однако, выразил сомнение в том, как еще не окончивший вузовского курса студент мог найти решение задачи, с которой не могли до тех пор справиться выдающиеся ученые-специалисты. Тем не менее, как мне потом рассказывали, в своих лекциях при изложении парадокса Гиббса он неизменно упоминал предложенное мною его решение.
Добавлю, что вскоре я занялся решением того же парадокса в области физической статистики (раньше речь шла о химической термодинамике). Здесь имелись работы, кроме самого Дж. Гиббса, — Л. Больцмана, М. Планка, А. Эйнштейна, И. Тамма и других.
После анализа парадокса и закона Дальтона в их статистической трактовке (это заняло несколько лет) я защитил первую диссертацию летом 1935 года в Институте общей и неорганической химии Академии наук СССР. Моим главным оппонентом был А. Раковский. Председательствующий на заседании ученого совета Н. Курнаков просил меня, как я пришел к своему решению? Я не стал входить в детали и ответил, что решение было уже заключено в исходной работе самого Дж. Гиббса, где выведение парадоксальной формулы для ?S целиком опиралось на закон Дальтона, так что требовалось лишь вспомнить об этом.
Я потому так подробно остановился на парадоксе и своих исканиях его решения, что это была единственная возможность привести достоверные свидетельства того, как функционировал ППБ, а главное, как он был преодолен благодаря подсказке-трамплину. Ведь все это я пережил сам, испытал на себе самом, а потом мог подробно и всесторонне проследить весь ход разгадки стоявшей задачи.
ППБ и трамплин при изучении каучука. Приведу случай, как в моей научно-химической практике был преодолен ППБ с помощью подсказки-трамплина. В 1938–1939 годах я попал в Научно-исследовательский институт резиновой промышленности (НИИРП) в лабораторию профессора Б. Догадкина. Последний дал мне аадание изучить вязкость натурального (импортного) жидкого каучука-латекса. При этом он сообщил, что, пользуясь вискозиметром Дэнлопа, он со своей сотрудницей (Поварской) обнаружил и изучил так называемую «структурную вязкость» каучука-латекса. Я с жаром принялся за работу. Изготовил тончайшие капилляры, измерил их размеры и начал экспериментировать. Но, кроме обычной, никакой «структурной», то есть дополнительной, вязкости не обнаружил.
Надо сказать, что при определении вязкости пользуются относительными выражениями: вязкость изучаемой жидкости относят к вязкости воды, принимаемой за единицу сравнения. Разумеется само собой, что этот масштаб должен оставаться все время постоянным.
Замечу, что при достаточно малом диаметре капилляра жидкость (скажем, вода) вытекает из него плавно, спокойной вертикальной струей, без внутренних завихрений. Но если диаметр трубки будет сильно увеличен, то в струе вытекающей жидкости начинаются завихрения (турбулентное движение), и это резко сказывается на времени истечения жидкости, по которому судят о вязкости этой жидкости. Поэтому всегда надо следить за тем, чтобы не происходило турбулентных явлений.
Так как я при всей тщательности проводимых экспериментов никак не мог обнаружить злополучную «структурную вязкость», то этим вызвал неудовольствие профессора и упрек, что плохо, дескать, работаю. «Вот мы, — сказал он, — пользовались куда более грубым прибором и все же легко и сразу обнаружили то, что вы никак не можете найти. Поищите хорошенько!»
Я еще раз прочел внимательно их работу, но никак не мог понять, откуда взялась так резко выраженная «структурная вязкость» каучукового латекса. Помню, что я долго думал над этим вопросом. А так как все время в голове вертелась эта штука, то она и стала мерещиться мне по всякому поводу то в виде каких-то утолщенных нитей, образующихся при вязании шерсти, то в виде неровно очиненного карандаша, то в виде разбухшей макаронины.
Однажды, сидя в институтской столовке, я увидел большой бугор на клеенке и по обыкновению подумал о том, что он похож на «структурную вязкость». Когда же я поднял клеенку, то обнаружил, что целая полоска от фанеры, покрывавшая крышку стола, отщепилась и образовала выступ. Сама же клеенка оказалась вполне гладкой, без всякого бугра. А так как перед тем у меня возникла мысль о «структурной вязкости», тот тут же появилась другая, как ее продолжение или подсказка, что, может быть, никакой «структурной вязкости» у латекса Б. Догадкин не обнаружил, а принял за таковую нечто совсем другое, коренившееся в процессах, совершавшихся в воде, а вовсе не в латексе, так же как и я неровность фанеры принял за утолщение самой клеенки.
Это и была подсказка-трамплин, с помощью которой и был преодолен ППБ. Я тут же занялся вискозиметром Дэнлона и обнаружил, что диаметр его металлической трубки настолько велик, что вода вытекает из него турбулентным потоком. К тому же ее внутренние стенки явно были шероховаты. Значит, никакой «структурной вязкости» с помощью такого прибора вообще обнаружить было невозможно. А то, что было принято за таковую, в действительности оказалось результатом искажения Данных о времени истекания воды из прибора; следовательно, эти данные никак не могли служить масштабом для определения относительной вязкости латекса. Ведь точно так же пешеход мог бы сказать, что стал идти вдвое быстрее, если его часы стали бы идти вдвое медленнее.
Я не буду подробнее анализировать, в чем здесь состоял ППБ, преодолению которого помог трамплин в виде клеенки в столовой, надеясь, что читатель сам его увидит.
Химическая подсказка решения одной математической задачи. Эта задача касалась определения числа отношений между понятиями. В «Философских тетрадях», отвечая на вопрос, «в чем состоит диалектика», В. И. Ленин отвечал: «Каждое понятие находится в известном отношении, в известной связи со всеми остальными».
Разумеется, В. И. Ленин имел в виду самые различные по своему характеру и содержанию отношения между понятиями. Но для начала встала задача ограничиться самыми элементарными отношениями, которые в логике именуются объемными и касаются лишь количественной стороны относимых друг к другу понятий.
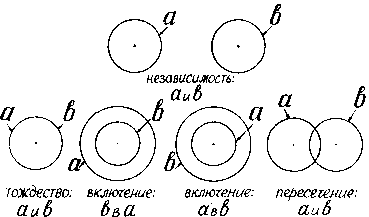
В простейшем случае для двух понятий существует, как известно, пять элементарно простых (объемных) отношений. Пользуясь геометрическими кругами, которые ввел в логику Л. Эйлер, легко установить пять отношений между двумя понятиями айв.
Встала задача определить теперь, сколько таких отношений может быть в случае трех, четырех и больше понятий; а в общем случае — n понятий.
Оказалось, что уже для трех понятий — а, в, с — это сделать чрезвычайно трудно, так как при наложении различных кругов друг на друга или их подсоединении друг к другу крайне трудно бывает установить, получаются ли одинаковые или разные системы из трех понятий. А для четырех, а тем более пяти и больше понятий практически это сделать невозможно. «В чем же дело?» — ломал я голову.
И тут неожиданно пришла подсказка из области истории органической химии, которой я подробно занимался, изучая труды К. Шорлеммера. Он писал, что первоначально к органическим причислялись такие вещества, которые получались из растительных и животных тел; иначе говоря, вещества классифицировались по их происхождению, генезису. Но в таком случае в число органических зачислялись многие неорганические только потому, что они встречались у живых существ, например, калий в растениях. Поэтому признак происхождения был отвергнут, и А. Лавуазье ввел аналитический признак химического состава: например, органическое вещество должно содержать углерод, отсюда органическая химия есть химия углеродистых соединений.
Когда я размышлял о том, почему не годится накладывание кругов друг на друга для определения числа отношений и понятий, я по ассоциации с органической химией увидел причину этого в том, что применяется генетический принцип (по происхождению), а не аналитический (по составу).
Теперь я могу сказать, что ППБ здесь состоял в привычке, начиная с Л. Эйлера, пользоваться обязательно геометрическими кругами, тогда как для большого числа понятий этот прием не годился. Химическая же подсказка, уловленная мною, указывала путь перехода от геометрических образов (по происхождению) к алгебраическим выражениям (по составу). И здесь мне снова помогла химия, а именно физико-химический анализ Н. Курнакова, которым я занимался экспериментально несколько лет в конце 20-х годов и теоретически в первой половине 30-х.
Согласно этому методу мы имеем дело с тремя категориями, характеризующими диаграмму «состав — свойства»: компонентами (в нашем случае а; в), фазами (а; в; ав) и системами, которые мы запишем так:
а + b ab ab + a ab + b ab + а + Ь
независимость; тождество; включение; включение; пересечение.
а и b а и b b в а а в b а и b
Как видим, здесь приведены те же пять отношений между двумя понятиями, которые были изображены выше посредством геометрических фигур, налагаемых друг на друга (по происхождению), здесь же они выражены алгебраическим способом (по их составу).
Так химия второй раз подсказала трамплин для преодоления существовавшего ППБ и для перехода к аналитическому (алгебраическому) способу описания отношений между понятиями.
Я не буду подробнее говорить о том, каким образом была вычислена мною общая формула для числа объемных отношений между n понятиями. Полученный мною результат я доложил на семинаре по математической логике, который вели профессора С. Яновская, П. Новиков и И. Жигалкин, одобрившие предложенное мною решение. Позднее его положительно оценил академик А. Колмогоров, после чего моя работа была опубликована.
* * *
Этим мы закончим затянувшийся разбор роли ППБ и трамплинов в ходе научных исследований и обратимся далее к выяснению их роли в ходе технических изобретений. Еще раз оговорюсь, что я так часто ссылался на свой весьма скромный личный опыт потому, что он позволил подробнее проследить действие подсказки-трамплина путем самонаблюдения, но отнюдь не по причине важности самих научных исследований, мною проведенных. Так я буду поступать и в дальнейшем.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК