6. Какие приемы облегчают нахождение логических ошибок
6. Какие приемы облегчают нахождение логических ошибок
Мы показали, какие правила необходимо знать для того, чтобы избежать логических ошибок. Однако одного знания правил логики недостаточно, как недостаточно знания правил грамматики для того, чтобы грамотно писать. Необходимо вырабатывать логические навыки правильного мышления. Наличие таких навыков позволяет правильно рассуждать, не поддаваясь действию разного рода аффектов, под влиянием которых возникают логические ошибки.
Иногда возражают, что человек может рассуждать правильно, совершенно не думая о логических правилах. Это верно. Если у человека уже имеется навык логичного мышления, то он рассуждает правильно, не думая о логических правилах, так же как человек, привыкший писать грамотно, не делает ошибок, хотя и не думает о грамматических правилах. Но навыки, позволяющие избегать логических ошибок, вырабатываются на основе знания логических правил с гораздо большим успехом, чем без них,
При отсутствии навыков, основанных на знании правил, человек не может быстро находить и точно квалифицировать логические ошибки. Это особенно относится к тем случаям, когда речь идет о малоизвестных или неизвестных вещах, когда ложность выводов не бросается в глаза.
Однако необходимо отличать неумение быстро найти и точно квалифицировать логическую ошибку в рассуждении от неумения определить, что в рассуждении есть какая-то, хотя и неизвестно какая, ошибка. В первом случае человек не сможет как следует понять сам и объяснить другим, почему та или иная мысль неправильна, почему нельзя доверять данному выводу. Во втором он вообще не будет видеть разницы между правильными и неправильными мыслями, будет доверять самым абсурдным выводам.
Если человек не имеет логических знаний, позволяющих ему быстро и четко определять сущность любой логической ошибки, если он не может показать, в какой мере и почему данное утверждение заслуживает или не заслуживает доверия, то было бы хорошо, если бы он умел, по крайней мере, тем или иным способом определять, что какая-то ошибка в рассуждении есть, поэтому целиком полагаться на него нельзя.
Для этой цели применяются некоторые приемы, с помощью которых, не зная твердо всех логических правил, можно установить наличие ошибки в том или ином рассуждении. Правда, эти приемы распространяются не на все рассуждения и не дают возможности квалифицировать ошибку, но они во многих случаях помогают избежать ошибки самому и заметить ее у других. В отдельных случаях с их помощью можно даже доказать, что данный вывод является неправильным.
Такие приемы мы неоднократно применяли в этой брошюре, когда хотели показать неправильность того или иного рассуждения. Они часто применяются и в повседневной жизни.
Применять их можно и даже необходимо, но нужно знать, в каких рамках это можно делать, к каким случаям применим и что дает каждый из этих приемов.
Самым универсальным и гибким из этих приемов является аналогия, которую можно применять к самым разнообразным случаям. Пусть мы имеем рассуждение: «Все планеты вращаются вокруг Солнца, следовательно, все тела, вращающиеся вокруг Солнца, — планеты». Как проверить правильность этого вывода, не зная правил обращения? Берем другое рассуждение, аналогичное первому по своей структуре, но имеющее вывод, истинность или ложность которого очевидна, например, «все воробьи — птицы, следовательно, все птицы — воробьи». Рассуждение это явно неправильно, следовательно, неправильно и аналогичное ему первое рассуждение.
Допустим, нам нужно проверить, правильно ли определение «школа — здание, в котором учатся школьники». Подбираем аналогичное определение, например, «Москва — город, в котором живут москвичи». Ошибочность определения во втором случае более очевидна, хотя оба они одного типа. Поэтому определение в том и другом случае дано неправильно. Пусть нам дан условно-категорический силлогизм:
если у человека повышенная температура, то он болен;
у него нет повышенной температуры;
————————————————————
следовательно, он здоров.
Верно ли это? Возьмем другое рассуждение, имеющее аналогичное строение;
если купленный в магазине продукт — колбаса, то этот продукт можно есть;
продукт, купленный в магазине, — не колбаса;
—————————————————————————
следовательно, его нельзя есть.
(Ясно, что колбаса — не единственный продукт, который можно есть). Поэтому оба рассуждения неправильны.
Выше таким же образом обосновывалась неправильность силлогизма:
все рыбы дышат жабрами;
кит — не рыба;
————————————
кит не дышит жабрами.
Другой силлогизм точно такого же строения дает явно абсурдный вывод, что доказывает неправильность всех силлогизмов такого типа:
помидоры съедобны;
огурцы — не помидоры;
————————————
огурцы не съедобны.
Частным случаем применения аналогии является использование графических схем для проверки правильности или неправильности тех или иных умозаключений. Здесь проводится аналогия между логическими и геометрическими отношениями. В самом деле, геометрическая фигура — круг, которым мы изображаем объем понятия, имеет совсем другую природу, чем это понятие. Например, понятие «тигр» имеет очень мало общего с кругом, так же как и понятие «животное». Но отношение по объему понятий «тигр» и «животное» аналогично отношению между кругами, из которых один составляет часть другого.
Рис. 13
С помощью графических схем можно наглядно показать соотношение понятий, входящих в рассуждение, и проверить, вытекает ли данный вывод при таком соотношении. Например, несостоятельность умозаключения
«все планеты вращаются вокруг Солнца;
Земля вращается вокруг Солнца;
—————————————————
Земля — планета»,
которая была выше выяснена другими способами, может быть показана и этим приемом. В первой посылке понятие «планеты» включается в понятие «тела, вращающиеся вокруг Солнца». Графически это можно изобразить так (рис. 13). Во второй посылке понятие «Земля» включается в понятие «то, что вращается вокруг Солнца». Изобразим понятие «Земля» точкой 3. Куда попадет эта точка? Конечно, она войдет в большой круг (рис. 14) на основании меньшей посылки. Но обязательно ли она попадет при этом в маленький круг — «планеты»? (рис. 15). У нас нет достаточного основания утверждать это. В посылках говорится только о том, что Земля должна войти в круг «тела, вращающиеся вокруг Солнца». Следовательно, делать отсюда категорический вывод «Земля — планета» будет неправильным. Земля — действительно планета, но из данных посылок это не вытекает.
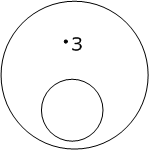
Рис. 14
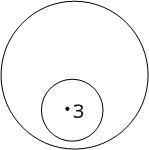
Рис. 15
Так же наглядно можно показать неправильность такого силлогизма (рис. 16):
все рыбы дышат жабрами;
киты — не рыбы;
————————————
киты не дышат жабрами.
В меньшей посылке говорится, что киты — не рыбы, значит, круги, изображающие тех и других, должны полностью исключать друг друга. При этом допускаются следующие возможности:
1) киты включаются в число дышащих жабрами;
2) киты полностью исключаются из числа дышащих жабрами;
3) часть китов дышит жабрами, часть — не дышит жабрами.
Можем ли мы выбрать только одну из этих трех возможностей для вывода о китах? Ясно, что нет. Никаких оснований у нас для этого нет.
Возьмем такое рассуждение:
«Бородин мог стать либо писателем, либо ученым, либо композитором. Он стал композитором. Следовательно, Бородин не был ни писателем, ни ученым».
Опыт показывает, что многие из тех, которые делают такой неправильный вывод, могут вместе с тем без особого труда справиться с задачей правильного — графического изображения отношений по объему понятий «писатели», «композиторы» и «ученые» (рис. 17).
Рис. 16
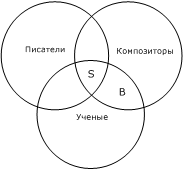
Рис. 17
А получив такую схему, уже совсем легко понять, что Бородин (B) в принципе мог быть одновременно и тем, и другим, и третьим (S). Кстати, он был ученым-химиком. В тех случаях, когда члены деления исключают друг друга, избежать ошибки значительно легче. Если этот человек может быть или пионером, или комсомольцем и известно, что он пионер, то ясно, что он не комсомолец (рис. 18).
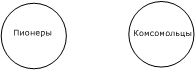
Рис. 18
В некоторых случаях можно определить правильность или неправильность рассуждения с помощью такого приема. Если плохо усвоены или забыты правила, которые должны соблюдаться в данной форме мысли, можно эту мысль свести к другой форме, правила которой известны лучше. Например, правила условно-категорического силлогизма усвоить и применять значительно легче, чем правила категорического силлогизма. Они очень просты и кратки: необходимый вывод получается от утверждения основания к утверждению следствия и от отрицания следствия к отрицанию основания. В остальных случаях — вывод лишь вероятный.
Предположим, нам нужно проверить правильность рассуждения
«планеты вращаются вокруг Солнца;
Земля вращается вокруг Солнца;
—————————————————
Земля — планета».
Это умозаключение — категорический силлогизм. Если мы забыли правила распределенности терминов в категорическом силлогизме, то мы можем свести его к условно-категорическому: «Если Земля — планета, то она вращается вокруг Солнца. Земля вращается вокруг Солнца. Следовательно, Земля — планета». Мы видим, что вывод делается от утверждения следствия к утверждению основания. Следовательно, умозаключение неправильное.
Другой пример:
все рыбы дышат жабрами;
кит не рыба;
————————————
кит не дышит жабрами.
После замены большей посылки получаем условно-категорический силлогизм: «Если кит — рыба, то он дышит жабрами. Кит — не рыба. Следовательно, кит не дышит жабрами». Вывод делается от отрицания основания к отрицанию следствия, следовательно, он является неправильным.
Возьмем силлогизм:
все честные люди против войны;
этот человек не против войны;
————————————————
этот человек не честен.
Преобразуем этот силлогизм в условно-категорический:
если человек честен, он против войны;
этот человек не против войны;
————————————————
он не честен.
Здесь вывод сделан от отрицания следствия к отрицанию основания. Следовательно, этот вывод с необходимостью вытекает из посылок и рассуждение является правильным.
Наконец, можно обнаружить, что в рассуждении есть какая-то ошибка, путем подбора определенного факта из жизни, несовместимого с данным выводом. Если этот вывод сделан из истинных посылок, то наличие такого факта явно будет указывать на наличие ошибки в рассуждении, например:
в правильно решенной задаче результат совпадает с ответом, данным в задачнике;
в этой задаче результат совпадает с ответом, данным в задачнике;
———————————————————————————————————
следовательно, эта задача решена правильно.
Если человек может привести хотя бы один такой факт или даже просто быть уверенным в возможности такого факта, когда в задаче, решенной неправильно, ответ совпадает с заданным, то тем самым он докажет, что вывод в данном случае сделан неправильно.
Разумеется, все эти приемы не могут заменить логических навыков, основанных на знании правил логики. Каждый из них по-своему ограничен и не может дать полной гарантии от ошибок в рассуждениях. Метод аналогии связан с необходимостью придумывать в каждом отдельном случае какой-то пример для сравнения, что удается далеко не всем и не всегда. К тому же применение аналогии без знания ее правил может привести к ошибочной аналогии. В результате сама проверка правильности рассуждения окажется неправильной. Применяя аналогию, нужно строго следить за тем, чтобы логическая форма того рассуждения, которое берется для сравнения, в точности совпадала с формой того рассуждения, правильность которого проверяется. В этом случае будет выполняться и первое правило аналогии о совпадении признаков или отношений в сравниваемых предметах и второе правило — о том, что если интересующий признак есть в одном предмете, то он есть и в другом. В самом деле, нас интересует в данном случае правильность вывода. А вывод в умозаключениях определяется, как мы знаем, исключительно строением умозаключения, его логической формой. Значит, если в умозаключении определенного строения вывод правильный, он обязательно будет правильным и в другом умозаключении, имеющем точно такое же строение. Другими словами, признак, сосуществующий с остальными признаками в одном предмете, сосуществует и в другом. Конечно, во многих случаях интуитивно удается подбирать правильные аналогии. Но это далеко не всегда. А ошибка в аналогии может привести к неправильному признанию или отрицанию того вывода, который проверяется с помощью этой аналогии.
Так, вывод «квадрат является равносторонним четырехугольником, следовательно, всякий равносторонний четырехугольник есть квадрат» является, несомненно, правильным. По аналогии с ним строится рассуждение «квадрат является фигурой с взаимно-перпендикулярными диагоналями, следовательно, всякая фигура с взаимно-перпендикулярными диагоналями есть квадрат». Однако ромб имеет взаимно-перпендикулярные диагонали, но ромб — это не квадрат. Следовательно, аналогия является неправильной. Почему? Потому что для сравнения взяты рассуждения, логически различные: в первом случае имеется общеутвердительное суждение, являющееся определением, поэтому его можно обращать в общеутвердительное; во втором случае — общеутвердительное суждение, не являющееся определением, поэтому его можно обращать только в частно-утвердительное: «некоторые фигуры с взаимно-перпендикулярными диагоналями — квадраты».
Все другие приемы также имеют свои недостатки.
Графические схемы можно применять в довольно ограниченном количестве случаев, так как далеко не все логические формы сводятся к отношениям объемов понятий. То же самое можно сказать и о сведении одних форм мышления к другим, как это было показано на примере категорических и условных силлогизмов. Сделать это бывает трудно, а часто и совсем невозможно. К тому же в процессе сведения может быть допущена логическая ошибка.
Наконец, ни один из этих приемов не дает возможности точно определять логическую сущность каждой ошибки и свободно ориентироваться в правильности и неправильности самых разнообразных рассуждений, выводов, доказательств и т. д. Действительную, по-настоящему высокую логическую культуру могут дать человеку только приобретенные прочные навыки правильного мышления, основанные на знании общих законов мышления и вытекающих из них логических правил.