9. Правдоподобность и поиск истины
9. Правдоподобность и поиск истины
Возьмем квадрат, представляющий класс всех высказываний, и разделим его на две равные подобласти — истинных высказываний (T) и ложных высказываний (F):
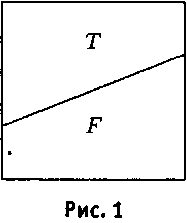
Изменим теперь немного нашу диаграмму, собрав класс истинных высказываний вокруг центра квадрата.
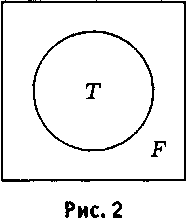
Задача науки, говоря метафорически, — покрывать попаданиями как можно большую часть мишени (T), то есть области истинных высказываний, и как можно меньшую часть области ложности (F), выдвигая теории или предположения, которые кажутся нам многообещающими.
Очень важно, чтобы в качестве предположений (conjectures) мы пытались выдвигать истинные теории. Однако истинность — не единственное важное свойство наших предположительных теорий, поскольку мы не очень заинтересованы в том, чтобы предлагать тривиальности или тавтологии. «Все столы — столы», несомненно, истина — более несомненная истина, чем ньютоновская или эйнштейновская теория тяготения, но она интеллектуально не волнует. Вильгельм Буш как-то сочинил то, что я назвал стихами для эпистемологической детворы[56]:
Дважды два четыре — верно,
Только пусто и легко.
Интереснее безмерно
То, что тяжко и полно.
Другими словами, мы ищем не просто истину — мы ищем интересную и просвещающую истину, мы ищем теории, предлагающие решения интересных проблем. Если это вообще возможно, то мы ищем глубокие теории.
Мы не просто пытаемся попасть в точку внутри нашей мишени T, мы хотим покрыть как можно более широкую и интересную область нашей мишени. Дважды два четыре, хотя это и истинно, не является в том смысле, который мы здесь имеем в виду, «хорошим приближением к истине» просто потому, что сообщает слишком малую часть истины, чтобы покрыть цель науки или даже ее существенную часть. Теория Ньютона является гораздо «лучшим приближением к истине», даже если она ложна (что правдоподобно), в силу громадного количества интересных и информативных истинных следствий, которые она содержит: ее истинностное содержание очень велико.
Существует бесконечное число истинных высказываний, и они имеют очень разную ценность (value). Один из способов их оценки — логический: мы оцениваем размер, или меру, их содержания (которое в случае истинных высказываний — но не ложных высказываний — совпадает с их истинностным содержанием). Высказывание, передающее больше информации, имеет большее информативное, или логическое, содержание — это лучшее (из двух сравниваемых) высказывание. Чем больше содержание истинного высказывания, тем лучше оно как приближение к нашей цели Tt то есть к истине (точнее, к классу всех истинных высказываний). Ведь мы стремимся узнать не только то, что столы — это столы. Когда мы говорим о подходе, или приближении, к истине, мы имеем в виду «ко всей истине», то есть ко всему классу истинных высказываний — классу T.
Если высказывание ложно, ситуация аналогична. Всякое недвусмысленное высказывание истинно или ложно (хотя мы можем и не знать, какая из этих двух возможностей фактически имеет место). Логика, которую я использую[57], имеет только эти два истинностные значения, и третьей возможности не дано. Однако одно ложное высказывание может показаться ближе к истине, чем другое ложное высказывание: «Сейчас 9.45 утра» кажется ближе к истине, чем «Сейчас 9.40 утра», если это замечание высказано в 9.48.
Однако в такой форме наше интуитивное впечатление ошибочно: эти два высказывания несовместимы и, следовательно, несравнимы (если только мы не введем меру вроде ct). Но в этой ошибочной интуиции кроется зерно истины: если мы заменим эти два высказывания интервальными высказываниями (см. следующий раздел), то первое действительно будет ближе к истине, чем второе.
Мы можем действовать следующим образом: первое высказывание заменяем высказыванием «Сейчас время между 9.45 и 9.48 утра», а второе — высказыванием «Сейчас время между 9.40 и 9.48 утра». Таким образом, мы заменяем каждое из наших высказываний таким, которое включает некоторую область последовательных значений (values) — область ошибки. В этом случае два замещенных высказывания становятся сравнимыми (поскольку из первого следует второе), причем первое действительно оказывается более близким к истине, чем второе; и это должно иметь место для любой непротиворечивой функции меры содержания, такой как ct или ctT- Поскольку в системе с функцией меры типа ctTнаши исходные высказывания сравнимы (в такой системе все высказывания в принципе сравнимы), мы можем заключить, что меру истинностного содержания можно определить так, чтобы ctT первого высказывания действительно было по крайней мере не меньше, — или даже больше, — чем у второго, что в известной мере оправдывает нашу первоначальную интуицию.
Заметим, что слово между в замещаюших высказываниях можно интерпретировать так, чтобы оно либо включало, либо не включало любую из границ области ошибки. Если мы интерпретируем его так, чтобы оно включало верхнюю границу, то оба высказывания истинны, и для обоих выполняется равенство ct = ctT. Они оба истинны, однако первое имеет большую правдоподобность, поскольку истинностное содержание у него больше, чем у второго. Если же мы интерпретируем между так, чтобы исключить верхнюю границу, то оба высказывания становятся ложными (хотя их можно назвать «почти истинными»), но остаются сравнимыми (не в смысле меры), и мы все еще можем — во всяком случае, я так думаю [58] — утверждать, что правдоподобность первого больше, чем второго.
Таким образом, не нарушая исходного принципа двузначной логики («всякое недвусмысленное высказывание либо истинно, либо ложно, и третьего не дано»), мы можем иногда говорить о ложных высказываниях, которые более или менее ложны, дальше от истины или ближе к ней. И эта идея более высокой или более низкой правдоподобности применима как к ложным, так и к истинным высказываниям: существенно здесь их истинностное содержание, а это понятие полностью входит в область двузначной логики.
Другими словами, похоже на то, что мы можем отождествить идею приближения к истине с идеей высокого истинностного содержания при низком «ложностном содержании».
Такое отождествление важно по двум причинам: оно снимает опасения некоторых логиков, связанные с использованием интуитивного представления (idea) о приближении к истине и позволяет нам сказать, что целью науки является истина — в смысле лучшего приближения к истине или большей правдоподобности.