§ 2. Некоторые ошибочные доказательства

§ 2. Некоторые ошибочные доказательства

Мы сможем более ясно осознать потребность в осторожном анализе умозаключений, если рассмотрим еще два примера исторически известных умозаключений.

1. Первый пример представляет попытку развить идеи Евклида. Свой великий труд «Начала» Евклид начал с двадцати трех определений, пяти аксиом (являвшихся недоказанными допущениями, общими для всех наук) и пяти постулатов (которые были недоказанными суждениями, относящимися только к геометрии). Пятый постулат (Книга I) является суждением о параллельных прямых, но Евклид не считал нужным его использовать до тех пор, пока не дошел до двадцать пятого суждения в своей книге. Если все другие аксиомы и постулаты Евклида представлялись его последователям самоочевидными, то пятый постулат, казалось, требовал доказательства. Прокл, математик V века, писал: «…тот факт, что когда уменьшаются прямые углы, прямые начинают сходиться, является истинным и необходимым; однако утверждение о том, что, поскольку они сходятся все больше по мере своего продолжения, они на определенном этапе пересекутся, является возможным, но не необходимым, если не будет предоставлен аргумент, показывающий истинность данного утверждения в случае прямых» [121] . На протяжении многих веков считалось, что введение пятого постулата без доказательства было серьезным недостатком «Начал», и осуществлялись множественные попытки его доказать.

Мы рассмотрим доказательство, предложенное Птолемеем и изложенное Проклом. Однако сначала нам нужно будет привести релевантные определения и постулаты Евклида. Согласно Евклиду (определение 23), параллельные прямые являются «прямыми линиями, которые находятся на одной плоскости и, будучи продолженными неограниченно в обе стороны, не пересекаются ни в одной стороне». Пятью постулатами являются следующие:

Постулат 1. От всякой точки до всякой точки можно провести прямую.

Постулат 2. Ограниченную прямую можно непрерывно продолжать по прямой.

Постулат 3. Из всякого центра всяким раствором может быть описан круг.

Постулат 4. Все прямые углы равны между собой.

Постулат 5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

Евклид ввел этот последний постулат для того, чтобы доказать суждение (теорему) 29: «Прямая, пересекающая две параллельные прямые, делает противоположные углы равными друг другу, а внешний угол равным внутреннему углу и противолежащему углу, а внутренние углы на одной и той же стороне равными двум прямым». Чтобы доказать постулат о параллельных прямых, Птолемей сначала доказал теорему 29 без помощи этого постулата, а затем показал, что постулат является следствием этой теоремы. Воспроизведем предложенное им доказательство теоремы:

Прямая линия, пересекающая две параллельные прямые, должна делать сумму внутренних углов на одной и той же стороне равной, большей или меньшей двум прямым углам.

Пусть АВ, CD – параллельные прямые, и пусть FG – секущая прямая. Я говорю, 1) что FG не делает внутренние углы на одной и той же стороне больше, чем два прямых.

Поскольку если углы AFG и CGF больше двух прямых углов, то оставшиеся углы BFG и DGF – меньше двух прямых.

Однако эти же два угла оказываются больше двух прямых углов, ибо AF, CG являются такими же параллельными, как и FB, GD, поэтому, если прямая, пересекающая AF, CG, делает внутренние углы больше двух прямых, то прямая, пересекающая FB, GD, также сделает внутренние углы больше двух прямых.

Однако эти же углы также и меньше двух прямых углов, ибо четыре угла AFG, CGF BFG, DGF равны четырем прямым углам, что невозможно.

Сходным образом 2) мы можем показать, что прямая, пересекающая две параллельные прямые, не делает внутренние углы одной и той же стороны меньше, чем два прямых угла.

Однако 3) если она не делает их ни больше, ни меньше двух прямых углов, то она может сделать внутренние углы на одной и той же стороне только равными двум прямым углам» [122] .

Обосновано ли доказательство Птолемея? Следует ли теорема 29 с необходимостью из приведенных аксиом и постулатов без пятого постулата? Рассмотрим более подробно рассуждение, которое мы выделили курсивом. Птолемей утверждает, что если мы допустим, что углы AFG, CGF больше двух прямых углов, то мы также должны допустить, что BFG, DGF также больше (равно как и меньше) двух прямых углов, поскольку все, что истинно для внутренних углов, находящихся на одной стороне секущей FG, с необходимостью одновременно истинно и для внутренних углов, находящихся на другой стороне секущей. Однако данное допущение не включено в постулаты. Птолемей защищает его, утверждая, что AF, CG также параллельны в одном направлении, как FB, GD в другом. Однако это просто сводится к утверждению о том, что через точку F можно провести только одну прямую, параллельную прямой CD. Данное допущение в точности эквивалентно постулату 5, который он и пытается доказать [123] .

Таким образом, доказательство Птолемея неудовлетворительно, и более тщательный анализ его рассуждения смог бы продемонстрировать ему, что это именно так. На самом деле мы знаем, что нельзя показать, что пятый постулат является необходимым следствием остальных постулатов, поскольку можно доказать, что он является независимым от остальных постулатов. Метод доказательства независимости разобран в главе VIII. На данном же этапе читателю следует обратить внимание на то, что строгое разложение аргумента на ряд шагов позволяет обнаружить все допущения, требующиеся для того, чтобы доказательство было обоснованным. Признание делаемых нами допущений и готовность исследовать все их возможные альтернативы являются отличительным признаком метода науки. Этот метод является единственной доступной нам гарантией от догматизма и самонадеянности.

2. Вторым примером значимого в историческом смысле «доказательства» является попытка доказать одно важное суждение в элементарной алгебре. Без сомнения, читатель знаком с правилом, согласно которому произведение двух отрицательных чисел всегда является положительным. Так, (-3) ? (-4) = (+ 12). Можно ли доказать данное суждение? Разумеется, доказательство будет возможным, только если другие суждения будут приняты в качестве посылок. Оказывается, что алгебра тоже может разрабатываться систематически на основании аксиом, относящихся к сложению и умножению количеств. Поэтому наш вопрос должен быть сформулирован следующим образом: можно ли доказать, что суждение о том, что произведение двух отрицательных чисел является положительным, является логическим следствием допущений, относящихся к сложению и умножению только положительных чисел?

К сожалению, систематический анализ алгебры является крайне абстрактным, и его понимание требует существенной интеллектуальной зрелости,

поэтому новичкам данный материал излагается просто в виде набора некоторых правил. Однако иногда осуществляются попытки приведения доказательств и для важных правил, и следующий аргумент зачастую приводится для обоснования суждения о произведении двух отрицательных чисел. Данный аргумент нацелен на то, чтобы показать, что правило умножения отрицательных чисел является необходимым следствием правил умножения и сложения положительных чисел.

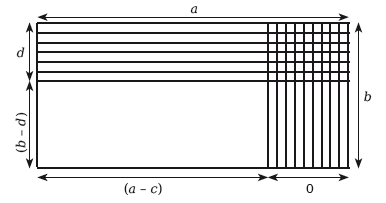
Приведенный выше четырехугольник имеет стороны а и Ь соответственно. Его площадь, согласно теореме планиметрии, равна ab. Площадь меньшего незаштрихованного прямоугольника со сторонами, равными (а – с) и (Ь – d) соответственно, равна (а – с)(Ь – d). Теперь выразим эту последнюю площадь в терминах большего прямоугольника и меньших заштрихованных прямоугольников. Анализ данной фигуры показывает, что площадь незаштрихованной фигуры может быть получена сначала путем вычитания из большого прямоугольника прямоугольника, который заштрихован вертикально (его площадь равна Ьс), а также горизонтально заштрихованного прямоугольника (его площадь равна ad), а затем путем прибавления прямоугольника, заштрихованного обоими способами (его площадь равна cd). Таким образом, мы можем записать уравнение 1:

(а – с)(Ь – d) = ab – be – ad + cd.

Далее припишем а и Ь значение нуль. Тогда мы получим уравнение 2:

(0 – с)(0 – d) = 0 ? 0 – 0 ? с – 0 ? d + cd;

или уравнение 3:

(-c)(-d) = (+cd).

В общем, заключением доказательства является положительное произведение двух отрицательных величин.

Является ли данное доказательство обоснованным? Читатель с легкостью увидит, что не является, поскольку уравнение 1 было развито на основе предположения, что а и Ь не равны нулю. Мы не можем получить уравнение 3 из уравнения 1, если не введем дополнительное допущение, что уравнение 1 будет истинным для всех возможных значений а и Ь. Однако это дополнение эквивалентно допущению о том, что все законы, распространяющиеся на сложение и умножение положительных чисел, также истинны и для отрицательных чисел. Но именно это суждение изначально и доказывалось.

На самом деле мы знаем, что правила оперирования отрицательных чисел независимы от правил оперирования положительных чисел. В очередной раз становится очевидной ценность разложения аргумента на составляющие его шаги. Точно так же как изучение допущений, требующихся для доказательства пятого постулата Евклида, привели Лобачевского и Больяя к открытию неевклидовых геометрий, так и исследование основополагающих правил алгебры привели сэра Уильяма Р. Гамильтона и Г. Г. Грассмана к открытию различных алгебраических систем. Без неевклидовых геометрий вряд ли было бы возможно развитие более сложной общей алгебры и современной физики. Важно отметить, что метод, требующий проявления всех требующихся для доказательства допущений, а также беспристрастные исследования всех альтернатив подобных допущений имеют далеко идущие следствия. Наилучший способ прояснить значимость логического метода для цивилизации – это задуматься о том, какую роль он сыграл в истории развития науки.

Данный текст является ознакомительным фрагментом.