Глава VII. Природа логической или математической системы

Глава VII. Природа логической или математической системы

1. Установите то, что нижеследующие постулаты являются непротиворечивыми. Также покажите, что они независимы друг от друга.

Постулат 1. Если а и Ь – различные элементы класса К, и < – некоторое отношение, то а < b или Ь < а.

Постулат 2. Если а < Ь, то а и Ь различны.

Постулат 3. Если а < Ь, то Ь < с, тогда а < с [134] .

2. Покажите, что набор операций (сложения, умножения, деления и вычитания) над целыми числами является изоморфным набору операций над дробями.

3. Обсудите отношение алгебры к аналитической геометрии в свете вопроса об изоморфизме.

4. Докажите, что аристотелевский принцип dictum de omni et nullo для категорического силлогизма является эквивалентным пяти аксиомам обоснованности, сформулированным в § 3 главы IV.

5. Покажите, что аксиома I для категорического силлогизма (средний термин должен быть распределен хотя бы единожды) является эквивалентной аксиоме 2 (ни один термин не может быть распределенным в заключении, если он не распределен в посылках).

6. «Напишите на одной карточке любое нечетное число, например 35, а на другой – любое четное, например 46. Попросите, чтобы кто-то дал одну карточку А, а другую – Б, но при этом так, чтобы вы не знали, у кого из них какая карточка. Ваша задача сообщить А о том, какое число написано у него на карточке. Скажите, чтобы А умножил свое число на любое четное, а В свое – на любое нечетное. Попросите А и В сложить получившиеся у них в результате умножения числа и назвать вам получившуюся сумму. Если сумма – четная, то у А изначально на карточке было нечетное число, если сумма – нечетная, то у А изначально было четное число» [135] . Докажите, что данный результат будет всегда сохраняться.

7. Покажите, что невозможно разложить целое число на множители, являющиеся простыми числами, более чем одним способом.

8. Что такое аксиома?

9. Что имеется в виду, когда утверждается, что суждение является самоочевидным?

10. Какого рода вопросы может задавать и разрешать логика относительно суждений?

11. Докажите с помощью математической индукции:

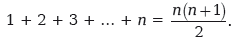
12. Прочитайте главы 6 и 7 «Введения в математику» Уайтхеда. Обсудите способы, которыми отличаются друг от друга целые, рациональные, действительные и мнимые числа.

Для дальнейшего изучения:

Younq J. W. Fundamental Concepts of Algebra and Geometry.

Chaps. II, III, IV, V.

Carmichael R. D. The Logic of Discovery. Chaps. II, III, IV, V, VI. Whitehead A. N. Introduction to Mathematics.

Jourdain R E. B. The Nature of Mathematics.

Russel B. Mysticism and Logic. Chaps. IV, V.