1. К вопросу модернизации математической теории

1. К вопросу модернизации математической теории

Для модернизации физической теории, как уже говорилось в разд. 1, необходимо, в первую очередь, создание сопряженной с актуальной действительностью матрицы научного поиска, то есть необходим переход к очередному структурному уровню философской концепции, который явится результатом интенсивного этапа в развитии философии, этапа изменения основ философской концепции с учетом уровня развития современного естествознания. Такой матрицей может стать представленная в первой части книги концепция мадэализма. Но модернизация естествознания невозможна без предварительной модернизации языка науки — математики. В рамках предлагаемой концепции можно сделать некоторые замечания по поводу возможных путей модернизации математической теории.

Модернизация математической теории, так же, как и физической теории, возможна только в союзе с философией. На важность и необходимость выбора правильных исходных общих посылок в изучении действительности указывали многие крупные ученые. Например, английский материалист XVII века Ф. Бэкон сравнивал философский метод с фонарем, который способен осветить путнику дорогу, чтобы он не заблудился. Без фонаря путник, в лучшем случае, может отыскать дорогу лишь ощупью. Любая частная наука, не опирающаяся на философию, «представляется чем-то крайне шатким». Аналогичной точки зрения придерживались выдающиеся исследователи Луи де-Бройль, М. Планк, А. Эйнштейн, великий русский физиолог И.П. Павлов, один из основоположников кибернетики Н. Винер и многие другие ученые (9,35).

Значение философии признают и представители математики. Так, например, Н. Бурбаки считает необходимым признать, что «точка зрения математиков на вопросы философского порядка, даже если эти вопросы имеют существенное значение для их науки, в большинстве случаев основана на мнениях, полученных из вторых и третьих рук и из источников сомнительной ценности» (8,21). Интересны высказывания на этот счет академика А.Д. Александрова. Он пишет, что «утверждение о ненужности диалектики, философии и прочее есть не более чем самодовольная некультурность, которую проявляет иной неразвитый «работяга», чванящийся тем, что «все эти теории не нужны»» (73,258). «Можно отметить тот исторический факт, что почти все действительно великие математики были философами-мыслителями. Философские принципы имеют огромное методологическое значение, обладают большой эвристической силой, дают возможность более интенсивно развивать специальные науки» (9,37).

Тесную взаимосвязь и взаимоопределенность этапов развития составляющих областей науки, в частности, философии, математики, естествознания, можно проиллюстрировать на примере разрешения одного из парадоксов науки — проблемы взаимоотношения прерывного-непрерывного и конечного-бесконечного.

Проблема анализа бесконечного впервые была рассмотрена в философии Древней Греции. Открытие этой проблемы приписывают Зенону Элейскому (около 450 г. до н.э.), который учил, что разум постигает только абсолютное бытие и что изменение есть только кажущееся. «Сформулированные Зеноном парадоксы ставили под сомнение реальность изменений и подчеркивали противоречия в понятиях движения и времени. Рассуждения Зенона вызвали сильное волнение философской мысли и можно даже говорить о «настоящем логическом скандале» — о кризисе греческой математики» (5,61).

Вслед за Зеноном Элейским, Платоном и Аристотелем проблема активно рассматривается в средние века Оригеном, Фомой Аквинским и другими философами-схоластами. «Ученые средневековья рассматривали понятия прерывного и непрерывного, конечного и бесконечного преимущественно в связи с философскими и физическими (анализ процессов движения) проблемами. Однако физика еще не стала экспериментальной наукой, математика не располагала достаточно удобным языком алгебраических обозначений, так что в логическом анализе понятий непрерывного и бесконечного схоласты четырнадцатого века оперировали в сущности тем же материалом, который был в распоряжении античной науки, и наталкивались на те же трудности» (5,112). В фундаменте проблем лежала неразработанность понятий «изменение» и «развитие» в философской науке.

«Мышление древних не знало идеи развития в точном смысле слова, так как время тогда понималось как протекающее циклически. Представление об абсолютно совершенном космосе, на которое опиралось античное мышление, исключало постановку вопроса о направленных изменениях, ведущих к возникновению принципиально нового. Идея направленности времени выдвигается в христианстве, которое относит ее лишь к сфере духа. Только в эпоху Возрождения с возникновением экспериментальной науки идея линейного направления времени распространяется на природу — формируется представление о естественной истории, то есть необратимых и направленных изменениях природных объектов. Это нашло выражение в космогонических гипотезах, а затем в теориях эволюции в зоологии и биологии» (13,400). Натурфилософские концепции Дж. Бруно, Н. Кузанского, И. Кеплера и Г. Галилея явились тем мировоззренческим фундаментом, опираясь на который Р. Декарт пришел к необходимости введения переменной величины в математическую теорию. Дальнейшее развитие математического языка описания движения, изменения привели к созданию Ньютоном и Лейбницем дифференциального и интегрального исчислений, которые базировались на сформулированных Декартом представлениях о переменной величине. «Поворотным пунктом в математике, — замечает в связи с этим Ф. Энгельс, — была Декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика и благодаря этому же стало немедленно необходимым дифференциальное и интегральное исчисление, которое тотчас и возникает и которое было в общем и целом завершено, а не изобретено, Ньютоном и Лейбницем» (7,573). Таким образом, именно становление понятий «изменение» и «развитие» в философской науке привело к изобретению исчисления бесконечно-малых в семнадцатом веке, которое в совокупности с теорией пределов, наконец, прояснило пути решения проблемы прерывного-непрерывного, конечного-бесконечного.

Но теория развития не остановилась на представлениях эпохи Возрождения. Глубокую философскую разработку она получила в немецкой классической философии XVIII—XIX в.в., особенно у Гегеля, «открывшего», по словам К. Маркса, и построившего диалектику как учение о всеобщем развитии духа. «Диалектический метод, — утверждает Гегель, — есть душа всякого научного развертывания мысли», именно он и только он «вносит необходимую внутреннюю связь в содержание науки» (53,63). Дальнейшую разработку, уже в материалистическом аспекте, учение о развитии получило в марксизме, трактующем развитие как универсальное свойство материи и, вместе с тем, как всеобщий принцип, служащий основой объяснения истории общества и познания. Показана всеобщность, универсальность диалектического механизма процессов развития. Однако до настоящего времени эти философские разработки не нашли адекватного отражения в математическом аппарате, то есть не «переведены» на язык науки и, соответственно, не доступны современному естествознанию.

Между тем одна из актуальнейших дискуссионных проблем современного естествознания — проблема «нарушения причинности», потери детерминизма на микроуровне, проблема соотношения причины и следствия (74). В собственно математике это так называемый «третий кризис основ», связанный с теорией множеств и соотношением части и целого (9). Проблемы части и целого возникли и в квантовой физике. Не имеют ли эти проблемы общих корней?

В каком же направлении искать пути выхода из кризиса? Может быть, исторически проверенным методом — использовать философию как матрицу научного поиска?

Используя историческую аналогию, можно предположить, что в математике должен появится новый теоретический уровень, который отразит универсальный всеобщий диалектический характер процессов движения, изменения, развития, совершающегося в соответствии со всеми требованиями развертывания диалектического противоречия. Тем самым математика переведет на язык науки тот потенциал диалектической теории, который накоплен человечеством за последние несколько столетий. В этом, конечно, есть серьезные трудности, так как «противоречие, — по словам Гегеля, — выступает непосредственно лишь в определении отношения. А в движении, импульсе и т.п. противоречие скрыто для представления за простотой этих определений». Но, тем не менее, «все вещи противоречивы в самих себе». «Противоречие — это имманентный источник движения, развития. Это принцип всякого самодвижения». «Противоречие — вот что на самом деле движет миром» (23).

Согласно мадэалистической концепции, в фундаменте любых процессов актуальной действительности лежит универсальный структурный «кирпичик мироздания» — структурный слой. Диалектика структурного слоя, рассмотренная в разделах 7.1 и 7.2, являясь отражением универсального механизма эволюции, заключает в себе мощный методологический потенциал. Появилась возможность создать эквивалентную конструкцию и в математической теории. Предположительно область математики, оперирующую формальными конструкциями такого рода, можно определить как «детерминальное» исчисление. Детерминальное исчисление позволит рассматривать статику и динамику причинно-следственных связей и сделать анализ соотношения части и целого. Детерминальное исчисление уже давно востребовано естествознанием, так как проблемы его (естествознания) модернизации связаны в свою очередь с проблемой модернизации математической теории как языка науки. Детерминальное исчисление предполагает введение новой математической символики, отражающей универсальный диалектический характер любых процессов. Следует заметить, что в истории математики нередко лишь благодаря новому способу записи становились возможными новые результаты, что отражает глубокую зависимость между содержанием и формой. Одним из примеров этого является введение индийско-арабских цифр, другим примером может быть символика Лейбница в анализе. «Лейбниц — один из самых плодовитых изобретателей символов. Немногие так хорошо понимали единство формы и содержания. На этом философском фоне можно понять, как он изобрел анализ: это было результатом его поисков «универсального языка», в частности языка, выражающего изменение и движение» (5,151). Подходящие обозначения лучше отражают действительность, чем неудачные, и они оказываются как бы наделенными собственной жизненной силой, которая, в свою очередь, порождает новое знание. Таким образом, возможно, требуется введение в математическую теорию новой символики, которая (в рамках детерминального исчисления) отразит универсальный диалектический характер процессов изменения, развития.

Интересно заметить, что в последовательности возникновения основных разделов математики проявляется закон отрицания отрицания (9,70) (см. схему).

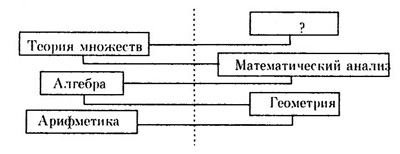
«Так, — пишет Н.И. Жуков, — создание системы символов для обозначения переменных величин в алгебре (работы Ф. Виета), введение буквенного коэффициента в уравнения представляет собой как бы возврат к арифметике, но на новой основе. В свою очередь, возникновение математического анализа есть не что иное, как распространение понятия переменной величины из области дискретного на область непрерывного с последующим освобождением функций от их геометрической интерпретации. Наконец, появление теоретико-множественного подхода определило перенесение центра тяжести снова на область дискретного» (9,70). Таким образом, следующий раздел математики должен перенести центр тяжести опять в область непрерывного, то есть исходить из теории множеств и иметь какие-то аналогии с разделом исчисления бесконечно малых. На наш взгляд, таким разделом может стать детерминальное исчисление.

Математической дисциплиной, наиболее близко подошедшей к осознанию необходимости символьного отражения диалектического характера процессов изменения, развития, является математическая логика. «Идея логического исчисления высказываний, суждений содержалась еще в трудах Лейбница (в работе «Искусство комбинаторики», например). Однако основы математической логики удалось заложить лишь в XIX веке Дж. Булю, который создал алгебру логики. Впрочем, его работы современниками всерьез не принимались и многими, даже видными, учеными рассматривались как простой курьез, плод досужего ума, в лучшем случае. Одновременно основы новой науки успешно разрабатывал А. Морган, но главным образом — Э. Шредер, так что начиная с конца XIX века она стала называться алгеброй Буля — Шредера. Большой вклад в ее дальнейшее развитие внесли П.С. Порецкий, Фреге, Пеано и, конечно же, известный философ Рассел, который совместно с А. Уайтхедом в начале XX века создал капитальный труд «Принципы математики». Именно с Фреге и Рассела начинается новый этап в развитии логики как исчисления. С середины XX века она получила особенно большое развитие в связи с успехами кибернетики и информатики и является ныне важнейшей областью математического знания» (9,59).

«В основе математической логики лежит исчисление высказываний и предикатов, в котором суждения обозначаются знаками, с которыми впоследствии можно оперировать как с обычными математическими символами. В кибернетике и информатике идут еще дальше: «атомарные» (далее неразложимые) высказывания обозначают буквами или знаками, а связки, рассматриваемые в качестве логических операторов, моделируют с помощью инверторов, конъюнкторов и дизъюнкторов, что позволяет для последующих исчислений использовать компьютер. Особого внимания заслуживает родство, общность математической логики с теорией множеств. Это обстоятельство дает право говорить о математической логике как об особой области современной математики, смыкающейся с теорией множеств» (9,60—61).

Современная математическая логика есть результат символизации и математизации традиционной логики, так что «и обычная, и математическая логика чаще всего обозначаются одним, более общим термином — «формальная»» (9,56). Она интерпретируется многими «как современный этап развития формальной логики» (9,57). Естественно узнать, почему математическая логика конца XX века базируется на построенной Аристотелем более двух тысячелетий назад формальной логике, игнорируя разработанную Гегелем менее двухсот лет назад диалектическую логику?

«Формальная логика, — пишет Н.И. Жуков, — наука о законах и формах правильного (последовательного и непротиворечивого) мышления. Только следование ее правилам делает рассуждения четкими, ясными и последовательными» (9,55). Но при этом далее уточняет: — «Однако адекватными действительности формами мышления будут те, которые являются предметом диалектической логики, способной выразить реальное противоречие внешнего мира, движение в объективной действительности» (9,56). Еще Ф. Энгельс отмечал, что «именно диалектика является для современного естествознания наиболее важной формой мышления, ибо только она представляет аналог и тем самым метод объяснения для происходящих в природе процессов развития, для всеобщих связей природы, для переходов от одной области исследования к другой» (7,367). Вот почему теория диалектики дает основополагающие принципы познания и преобразования действительности, являясь универсальной методологической, «принципиальной, выверенной основой естественнонаучного и социального познания» (9,55).

Таким образом, признается определяющая роль именно диалектической логики. Проблемы же математизации диалектики связаны с противоречием мышления и языка. Как пишет Н.И. Жуков: — «Прерывно-непрерывный процесс мышления, в котором адекватно отображаются явления внешней действительности, осуществляется в дискретных по своей форме сложных знаках — словах естественного языка. Для формальной логики понятия есть нечто неизменное, статичное и дискретное (соответствующее языку, но противоречащее мышлению). Данное реальное противоречие языка и мышления, в общем случае противоположность дискретного и непрерывного, будучи главной причиной основного различия между диалектикой и формальной логикой, порождает парадоксы… и в математике, и в логике, которая является необходимым способом ее построения, средством формально-дедуктивного метода» (9,67). «В движении понятий, — пишет Н.И. Жуков, — в их гибкости схватывается движение, присущее всем без исключения объектам внешнего мира, но в силу особенностей формальной логики, правила которой должны выполняться в каждом акте мышления, происходит раздвоение единого на противоположности, фиксация отдельных сторон движения, в частности, вычленение устойчивости и дискретности в прерывно-непрерывном процессе мышления. Подобная дихотомия и приводит к возникновению парадоксов. Следует заметить, что речь при этом идет об огрублении диалектических, а не формально-логических понятий. Последние, как показали еще Гегель и Кант, фиксируют только одну из двух противоположных сторон движения объектов реальной действительности и соответствующих ему диалектических понятий — устойчивость и дискретность. В результате этого и возникает неожиданная на первый взгляд ситуация: избегая противоречий, формальная логика и дискретная математика сами неизбежно порождают своеобразные коллизии в виде парадоксов. Такова цена точности, непротиворечивости и однозначности в математике и формальной логике» (9,68).

Таким образом, можно утверждать, что математическая теория вплотную подошла к осознанию необходимости построения математического аппарата, отражающего диалектический механизм процессов развития, изменения, и остановилась в нерешительности. По этому поводу можно привести высказывание Ф. Энгельса: «Великая основная мысль, — писал Ф. Энгельс, — что мир состоит не из готовых, законченных предметов, а представляет собой совокупность процессов, … эта великая основная мысль со времени Гегеля до такой степени вошла в общее сознание, что едва ли кто-нибудь будет оспаривать ее на словах, другое дело — применить ее в каждом отдельном случае и в каждой данной области исследования» (14,302). Сказано больше века назад, а как актуально звучит в наше время!

Таким образом, применить диалектику в области математической теории, преодолеть противоречие между языком и мышлением — актуальнейшая задача современности, требующая, с т. зрения мадэализма, максимальной концентрации интеллектуальных сил.

При этом, возможно, произойдет и обратный эффект: давно назревшее внедрение математических методов в философскую науку. Очевидно, что математизация практически любой отрасли знаний ведет к ее прогрессивному развитию. Не случайно К. Маркс, по словам П. Лафарга, отмечал, что «наука только тогда достигает совершенства, когда ей удается пользоваться математикой» (75,66). «Современная философия, как правило, не пользуется математикой, хотя в самой философии нет существенных препятствий для применения математики. В самом деле, круг вопросов, составляющих ее главный интерес, не накладывает каких бы то ни было ограничений на методы их решения. История знает немало примеров «математической философии». Это и пифагореизм, и древнекитайские учения, и изыскания Декарта, Лейбница, Луллия и многое другое. Правда, результаты этих поисков, по-своему интересные, по некоторым причинам не привлекли в дальнейшем серьезных исследователей и не стали, к сожалению, достоянием современной философии» (69,46). Одна из причин состоит в том, что они не могли опереться на соответствующий уровень математического аппарата. Детерминальное исчисление, возможно, и будет представлять собой этот необходимый уровень.