3.4. Математическая структура как модель актуальной действительности

3.4. Математическая структура как модель актуальной действительности

Что такое познание? Полезно вспомнить высказывания В.И. Ленина, записанные им по поводу учения о понятии в «Науке логики» Гегеля: «Познание есть отражение человеком природы. Но это не простое, не непосредственное, не цельное отражение, а процесс ряда абстракций, формирования, образования понятий, законов, каковые понятия, законы (мышление, наука = «логическая идея») и охватывают условно, приблизительно универсальную закономерность вечно движущейся и развивающейся природы» (6,164). Там же: «абстракции отражают природу глубже, вернее, полнее. От живого созерцания к абстрактному мышлению и от него к практике — таков диалектический путь познания истины…» (6,152). Абстрактное мышление, создание теории, изучение свойств понятий не отрывает познание от действительного мира, а позволяет, если только они правильны, познавать его глубже, является необходимым шагом любого познания.

Согласно основным принципам диалектики, все процессы и явления объективной действительности глубоко взаимосвязаны друг с другом (принцип взаимосвязи), причем в соответствии с принципом развития, изменения, связи эти динамические. Суть процесса познания можно определить как вскрытие, определение этих динамических связей объективной реальности, отражение «универсальной закономерности вечно движущейся и развивающейся природы» тем или иным методом. Одни из таких универсальных методов познания — моделирование связей при помощи определенного набора модельных элементов (например, чисел или других знаков), т.е. создание модельных структур, отражающих способ связи элементов, преобразование этих модельных структур в соответствии с законами преобразования, сохраняющими связи неразрывными, получение новых структур, новых совокупностей связей и соотнесение этих новых связей с объективной действительностью.

В качестве средства абстрактного моделирования при помощи набора символов и правил их объединения выступает математика. Математика является значительно большим, чем наука, поскольку она есть, по выражению Н. Бора, язык науки (29). «Определяющим признаком всякой математической дисциплины всегда является некоторый формальный метод, потенциально допускающий самые различные материальные воплощения, а следовательно, и практические применения. Может ли тот или иной предмет, то или иное явление реального мира быть исследовано с помощью данного математического метода — этот вопрос решается не конкретной природой данного предмета или явления, но исключительно их формальными структурными свойствами и прежде всего теми количественными соотношениями и пространственными формами, в которых они живут или протекают» (103,9).

Каков же предмет исследований математики? Согласно Ф. Энгельсу, «чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира» (7,37). Н. Бурбаки утверждают, что «единственными математическими объектами становятся, собственно говоря, математические структуры» (8,251). С этой группой французских математиков можно согласиться. Но откуда берутся эти структуры и какое отношение они имеют к миру действительности? Если это абстракции некоторых сторон реального мира, то позиция Бурбаки вполне согласуется с точкой зрения Ф. Энгельса. Сами Н. Бурбаки писали, что «…основная проблема состоит во взаимодействии мира экспериментального и мира математического. То, что между материальными явлениями и математическими структурами существует тесная связь — это, как кажется, было совершенно неожиданным образом подтверждено недавними открытиями современной физики, но нам совершенно неизвестны глубокие причины этого, и быть может, мы их никогда не узнаем» (8,258). Это пессимистический вывод, и, по мнению акад. Б.В. Гнеденко (103), он означает только то, что Н. Бурбаки лишь поверхностно затронули важнейший вопрос: каков объект изучения математики. Они не попытались выявить процесс формирования основных понятий и основных задач математики в историческом аспекте. Подобные вопросы не могут возникнуть в связи с определением Ф. Энгельса, поскольку в нем уже содержится утверждение о том, что математические понятия являются лишь абстракциями от некоторых отношений и форм реального мира, они берутся из реального мира и поэтому естественным образом с ним связаны. В сущности этим объясняется поразительная применимость результатов математики к явлениям окружающего нас мира, объясняется успех того процесса, который мы сейчас наблюдаем и который называется «математизацией» знаний. «Удивительная, непостижимая эффективность математики в естествознании, тот факт, что ее современные модели зачастую описывают довольно неплохо сложные процессы материальной действительности, говорит о том, что математика отражает не только количественную, но и в какой-то мере качественную сторону явлений объективной действительности, о чем писали еще Кант и Гегель» (9,16).

Если проанализировать состояние современной математики как области науки, как языка науки в историческом аспекте, выявить процесс формирования основных понятий, то становится очевидным, что современная математика имеет логически стройную структуру, элементами которой являются, в свою очередь, те самые математические структуры, поразительная применимость которых так удивляет («принцип иерархии структур» по Н. Бурбаки). В этой связи возникает вопрос — не отражает ли общая структура современной математики глубинную, фундаментальную структуру действительности? Не является ли внутренняя структура математики моделью актуальной действительности? Если это так, то открывается уникальная возможность взглянуть на актуальную действительность через призму структуры современной математики. Итак, что же лежит в основе современной математики?

В соответствии с исследованиями школы Н. Бурбаки, фундаментом современного математического знания является теория множеств. «Возможно вывести почти всю современную математику, — пишет Бурбаки, — из единого источника — теории множеств» (10,26). Таким образом, можно предположить, что в фундаменте логической структуры математики лежат два понятия — понятие «множество» и понятие «отношение». «Множество» есть совокупность элементов. Элемент множества — основная структурная единица при моделировании актуальной действительности средствами математики. Понятие «отношение» отражает наличие связей между элементами множества. Совокупность элементов множества и связей, отношений между ними образуют конкретную математическую структуру (11). Так, если задать некоторое множество элементов, то отношение (другой термин — закон композиции) между собственными элементами этого множества определяют как внутреннее (унарное, бинарное, тернарное — в зависимости от количества элементов). Если же в отношении участвуют элементы разных множеств, то такой закон композиции определяется как внешний для этих множеств. Простейшая математическая структура — группоид — задается как множество элементов с заданным на нем внутренним бинарным законом композиции (11,62). Можно определить закон композиции на структурном уровне, единичным элементом которого является группоид. Для этого вводят понятие «гомоморфизм», которое отражает связи между группоидами (как разновидности — «изоморфизм», «эндоморфизм» и др.). «Группа» — частный случай группоида. Последующие уровни иерархии математических структур: «кольцо» — множество с заданными на нем двумя законами композиции (группа с дополнительными связями), «тело» — множество с заданными на нем двумя группами, «векторное пространство» — конструкция на основе группы, тела и закона композиции между ними, «тензор», «спинор», «твистор» и др. (11). Получается иерархическая последовательность математических структур, в которой новые структуры формируются путем задания отношений, связей между объектами предшествующих уровней сложности.

Как видим, в математике проявляется логически стройная структура, в которой всякий отдельный структурный уровень определяется своим единичным элементом, который, в свою очередь является сложной математической структурой по отношению к нижнему (по степени сложности) структурному уровню, но является составной частью элемента верхнего структурного уровня. Иными словами, единичный элемент очередного структурного уровня — это совокупность элементов предыдущего с заданным на нем отношением (связями между элементами). Как единое целое, этот элемент является, в свою очередь, единичным элементом для формирования следующего структурного уровня. Общий принцип иерархии математических структур можно схематично представить следующим образом:

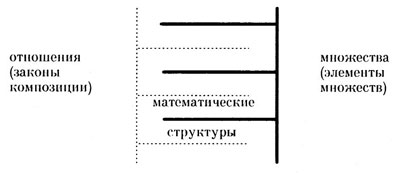
Таким образом, в современной математике можно выделить явно выраженную внутреннюю иерархическую структурность. Не может ли она отражать структуру актуальной действительности?