Глава VI. Обобщенная или математическая логика
Глава VI. Обобщенная или математическая логика
1. Укажите, какое отношение имеет место в каждом из следующих примеров: транзитивное, интранзитивное, симметричное, асимметричное, одно?однозначное, одно?многозначное или много?многозначное.
a. Он самый низкорослый в армии.
b. Джозеф имел тех же родителей, что и Бенжамин.
c. Адам является предком всех нас.
d. Нетерпение не является свойством хорошего преподавателя.
e. Смит является соседом Джонса.
f. Россия потерпела поражение от Японии.
g. Ромео – возлюбленный Джульетты.
h. Агент по продаже билетов знаком со многими знаменитостями.
i. Браун – наемный работник Джексона.
2. Обсудите содержание данного отрывка:
«Крайне ошибочным трюизмом, считающимся прописной истиной и повторяемым в речах высокопоставленных людей, является утверждение о том, что мы должны вырабатывать привычку думать о том, что мы делаем. На самом же деле, происходит обратное. Цивилизация развивается, увеличивая количество важных операций, выполнять которые мы можем, не думая. Мысленные операции подобны кавалерийским расчетам при сражении – их число крайне ограничено, им требуются свежие лошади и задействоваться они должны исключительно в решающих ситуациях» [133] .
3. Сформулируйте следующие выражения словами и упростите их:
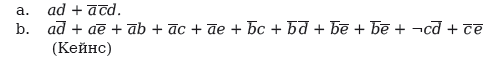
4. Покажите, что:
5. Приведите суждения, противоречащие данным:
6. Приведите суждения, противоречащие данным:
a. Цветущие растения являются либо эндогенными, либо экзогенными, но ни то и другое одновременно.
b. Цветущие растения являются васкулярными, а также являются либо эндогенными, либо экзогенными, но ни то и другое одновременно.
7. Назовите некоторые сложности использования разговорного языка для отдельных целей науки.
8. Проверьте по толковому словарю изменение в значении таких слов, как «вид», «рукопись», «часы», «род», «доктор».
9. Что означает класс?
10. Что означает логическая сумма двух классов? Логическое произведение двух классов?
11. Что означает утверждение, что один из двух классов включен в другой?
12. Что такое нуль-класс и каковы отношения между этим классом и любым другим классом?
13. Выразите нижеприведенные суждения в символической форме:
a. Только настойчивые добиваются успеха.
b. Некоторые профессора не являются седыми.
c. Никто, кроме молодых, не способен на героизм.
d. Все книги по логике содержат опечатки.
e. Ни один спортсмен не живет долго.
14. Докажите в символической форме:
a. Все а суть Ь; следовательно, все не-b суть не-а.
b. Ни один а не является Ь; следовательно, все а являются не-Ь.
c. Некоторые а суть Ь; следовательно, некоторые Ь суть а.
d. Некоторые а не суть Ь; следовательно, некоторые не-Ь не суть не-а.
15. Выразите в символической форме:
a. Если р имплицирует q, a q имплицирует г, то р имплицирует г.
b. Если р и q имплицируют г, то р и не-г имплицируют н e-q.
c. Если р или q имплицирует г, то либо р имплицирует г, либо q имплицирует г.
Для дальнейшего изучения:
Couturat L. Algebra of Logic.
Whitehead A. N. Universal Algebra, Bk. I, Chap. I and Book II. Lewis С. I., Langford. Symbolic Logic.
Eaton R. M. Symbolism and Truth. Chap. VII.
О природе символов:
Johnson W. E. Logic, Part II. Chap. III.
Whitehead A. N. An Introduction to Mathematics. Chap. V.
Eaton R. M. Symbolism and Truth. Chap. II.
Данный текст является ознакомительным фрагментом.