Знаки-символы

Для этих типов знаков знаковые действия не тождественны действиям с объектами Х, которые знаки-символы замещают. Если, например, мы рассмотрим процесс «сложения» чисел 1 и 2 (1+2=3), то увидим, что эта операция по своему строению не имеет ничего общего с объединением в пространстве двух реальных совокупностей, что, скажем, имеет место, когда складываются два числа древних египтян | и || (к числу | присоединяют число || и получают число |||). Примером знаков-символов могут служить не только современные числа, но и число 10 древних египтян – ?, и шумеров – ?. Нетрудно заметить, что эти числа не представляют собой совокупности из десяти элементов, их нельзя пересчитать или разбить на части. Хотя на более раннем этапе египетское число 10 представляло собой именно десять черточек – ||||||||||.

Знаки-символы могут использоваться, во-первых, для тех же целей, что и знаки-модели (например, счета), во-вторых, для осуществления различных формальных операций (умножение, деление, сложение, вычитание и пр.), в-третьих, они подобно знакам-символам могут стать самостоятельными объектами. Рассмотрим одну иллюстрацию – использование египетских чисел для пересчета военного отряда, построенного в 7 шеренг, в каждой из которой стоит по 12 воинов. Сначала египетский писец пересчитывает количество шеренг и число воинов в каждой шеренге. Затем перемножает число 7 на 12 (в древнем Египте умножение осуществлялось путем многократного сложения и удвоения чисел). Слева я записал операцию умножения, как она делалась в Египте, а справа для понимания современными числами:

Теперь ту же деятельность я изображу как действия со знаками-символами С.

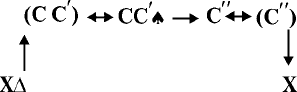
(схема 5)

Здесь Х – количество воинов в отряде, С и С' – числа 7 и12, ? – операция египетского умножения, С' – результат умножения, число 84.

Рассмотрим происхождение некоторых видов знаков-символов, например, как могло сложиться египетское число 10. Сначала, как я уже отмечал, числа записывались с помощью определенного количества черточек, т. е. знаков-моделей М. Однако при подсчете больших совокупностей предметов и операциях с соответствующими числами возникали проблемы: не хватало писчего материала, а простые действия сложения, вычитания, деления на равные части или умножения были исключительно утомительными и долгими. Здесь на помощь приходят вспомогательные (разделительные) знаки. Поскольку единицей устного счета была десятка, в практике совокупности чисел М (в нашей интерпретации – это знаки-модели) стали разбивать на группы из десяти элементов (десять человек составляли единицу в войсках, налог сдавали и собирали по десяткам единиц и т. п.). Разбитые на десятки числа М подобно прочим числам «складывались», «вычитались», «делились» на равные части. Чтобы не путать одни десятки с другими, каждая группа из десяти элементов отделялась от других специальным иероглифом – ?.

Эти иероглифы выступали в роли особых знаков С, которые можно отнести к знакам-индексам. Когда возникли указанные выше трудности с большими числами, вместо того, чтобы действовать со знаками-моделями стали работать со знаками-индексами, поскольку их было в десять раз меньше, чем чисел.

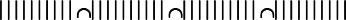
(схема 6)

Здесь М' – числа, разбитые на десятки, С – иероглифы, разделяющие десятки между собой.

С изменением употребления знаков-индексов С постепенно изменился и взгляд на их природу: эти знаки начинают пониматься тоже как числа, но особые – каждое новое число рассматривается как эквивалентное старому числу |||||||||| (десять). Другими словами, знак С (о) начинает обозначать определенный знак М (число десять), т. е. становится знаком-символом. Получается, что знаки-символы фиксируют содержания, сложившиеся на основе употребления знаков-моделей.