Отношения между объемами понятий

Если мы попытаемся сравнить между собой объемы различных понятий, то сразу же заметим, что у одних понятий объемы большие, у других — поменьше, что объем одного понятия может включаться в объем другого понятия и т. п. Однако сначала мы обнаружим, что некоторые понятия вообще невозможно сравнивать с этой точки зрения — настолько далеки они друг от друга по своему содержанию. Ну как, в самом деле, сравнивать понятия «оперная ария» и «дерево», «время года» и «бифштекс»?! Такие понятия, в содержаниях которых нет ничего общего, называются несравнимыми.

Сравнимыми называют понятия, содержания которых имеют общие элементы, т. е. имеются какие-то свойства, черты, признаки, которые входят в содержание как одного, так и другого понятия. В дальнейшем мы будем говорить только о сравнимых понятиях.

Совместимыми называются понятия, объемы которых имеют общие элементы, т. е. существуют предметы, которые включаются в объем как одного, так и другого понятия. Будем изображать объемы понятий в виде кругов, в центре которых стоит буква, представляющая некоторое понятие, например, объем понятия A (скажем, «слон») будет выглядеть так:

Этот кружок включает в себя всех слонов, живущих на Земле. Тогда с помощью этих кругов мы можем представить следующие отношения между совместимыми понятиями:

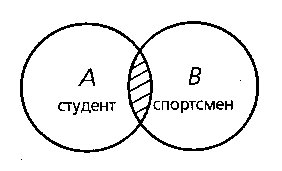
Пересечение

Объемы двух понятий A и B имеют общую часть — это те студенты, которые одновременно занимаются спортом, и те спортсмены, которые учатся в вузе. В то же время есть студенты, не занимающиеся спортом, и спортсмены, которые не являются студентами.

Подчинение

Объем понятия B полностью включается в объем понятия A, например, объем понятия «дуб» полностью включается в объем понятия «дерево». Иногда отношение подчинения называют «родо-видовым» отношением: более широкое по объему понятие A называют «родом», а понятие B называют «видом».

Тождество

Объемы понятий A и B совпадают, т. е. это одна и та же совокупность предметов, отображаемая с точки зрения разных существенных свойств двумя понятиями, например: «первый космонавт» и «Ю.А. Гагарин», «квадрат» и «равноугольный ромб», «храбрый» и «смелый».

Несовместимыми называются понятия, объемы который не имеют общих элементов, т. е. нет предметов, которые одновременно включались бы как в объем одного, так и в объем другого понятия. Существует три разных отношения между объемами таких понятий.

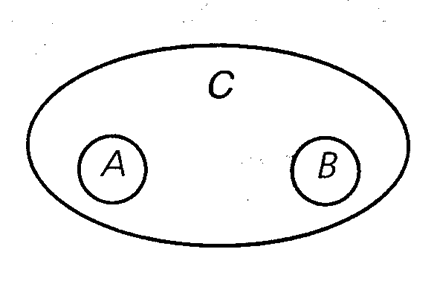
Соподчинение

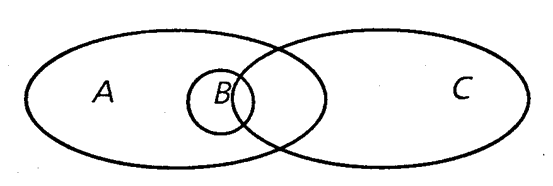
Объемы понятий A и B полностью различны, но они все-таки сравнимы, т. е. имеют в своих содержаниях какие-то общие черты. Именно это мы и имеем в виду, когда помещаем их в объем третьего, более широкого понятия C, видами которого являются наши несовместимые понятия. Например, понятие A — «дуб», понятие B — «береза». Эти понятия не имеют общих элементов, нет предмета, который одновременно был бы и дубом и березой, однако и дубы, и березы включаются в объем более широкого понятия «дерево» (C).

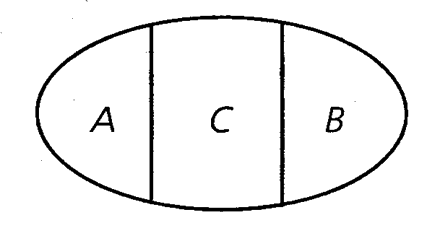
Противоположность

Выше нам было безразлично, как именно располагаются наши дубы и березы в объеме понятия «дерево». Но иногда это имеет значение, ибо предметы, входящие в объемы сравниваемых понятий, стремятся как можно дальше отодвинуться друг от друга, как бы тяготеют к разным полюсам в объеме третьего родового понятия. Например, «богатые» — «бедные», «трусливые» — «храбрые», «здоровые» — «больные» и т. п. Такие понятия называются «противоположными».

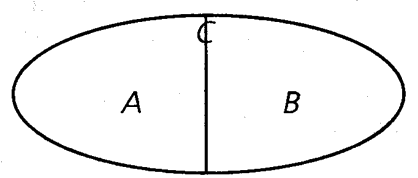
Противоречие

Два сравниваемых понятия не просто тяготеют к разным полюсам в объеме третьего понятия, но вместе полностью исчерпывают объем этого третьего понятия, например, «богатый» — «небогатый», «здоровый» — «нездоровый» и т. п. Такие понятия называются «противоречащими» друг другу. При выражении противоречащих понятий в языке одно из них содержит, как правило, отрицательную частицу: «неумелый», «невежливый», «невысокий» и т. п. Отличить противоположность от противоречия нетрудно: противоположные понятия оставляют между своими объемами некоторую «прокладку», т. е. те предметы, которые не включаются ни в первое, ни во второе понятие; противоречащие понятия полностью исчерпывают объем третьего, более широкого понятия.

Порой бывает полезно с помощью этих простых схем наглядно представить себе отношения между объемами тех или иных понятий. В каком, например, отношении находятся следующие понятия:

A — врач,

B — хирург,

C — женщина.

Берем первую пару понятий. Каково отношение между врачами и хирургами? Пересечение? Нет, ибо тогда часть хирургов окажется вне круга врачей. А что это за хирурги, которые не являются врачами? Бандиты! Все хирурги должны войти в число врачей. Тогда между объемами этих понятий должно быть отношение подчинения: все хирурги врачи, но не все врачи — хирурги. Теперь можно приняться за женщин. Могут женщины быть хирургами? Могут. Могут женщины быть врачами других специальностей — терапевтами, отоларингологами, психиатрами? Могут. А могут ли они быть просто женщинами, не врачами? Еще как могут! Тогда круг женщин пересекаем с обоими кругами:

Рисование кружков кажется детским занятием. Однако оно полезно в том отношении, что заставляет нас задуматься над содержанием даже хорошо известных нам понятий. Смысл, содержание многих слов мы схватываем довольно поверхностно, поэтому плохо представляем себе, к каким объектам они относятся. Пытаясь точно представить отношения между объемами понятий, мы гораздо яснее и глубже начинаем понимать их содержание. Попробуйте изобразить отношения между объемами очень хорошо известных вам понятий: 5) мать — дочь — бабушка — женщина, и вы убедитесь, как мало мы вдумываемся в значения этих слов!

Пора немного подумать! Многие из вас помнят детскую задачку о волке, козе и капусте, которых нужно было по очереди перевезти на другой берег реки и при этом не допустить, чтобы коза съела капусту, а волк сожрал козу. Она представляет собой упрощенный вариант довольно старой задачи, имеющей множество сложных вариантов. Вот один из них.

6) На берег реки приехали 3 рыцаря, каждый со своей дамой. У берега реки стоит лодка, способная вместить не более двух человек. Как с помощью этой лодки рыцарям и их дамам переправиться на другой берег, если должно быть выполнено условие: ни одна дама не может оказаться в обществе других рыцарей, если рядом с ней нет ее собственного рыцаря? Лошади переплывают реку сами, дамы способны грести веслами не хуже рыцарей, в лодку входят и из нее выходят по одному, лодка может пересекать реку сколько угодно раз, обратно лодку кто-то должен пригнать и т. п. Не выдумывайте ситуаций, когда кто-то прыгает из лодки на берег, а с берега другой прыгает в лодку и оказывается, что оба парят в воздухе!

Попробуйте найти хотя бы один способ переправы.