§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ

§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ

Сложные суждения, как и простые, могут быть сравнимыми и несравнимыми.

Несравнимые — это суждения, которые не имеют общих пропозициональных переменных (простых суждений). Например, р ? q и m ? n.

Сравнимые — это суждения, имеющие одинаковые препозиционные переменные (простые суждения) и различающиеся логическими связками, включая отрицание. Например, сравнимыми являются два суждения: «Норвегия или Швеция имеют выход в Балтийское море» (р ? q); «Ни Норвегия, ни Швеция не имеют выхода в Балтийское море» (?р ? ?q). Хотя эти суждения различны по логической форме (первое из них — дизъюнктивное суждение, а второе — конъюнкция отрицаний, вместе с тем они сравнимы, поскольку включают одинаковые составляющие (простых суждений) (р и q). Сравнимы следующие пары суждений: 1) р ? q и ?р ? q; 2) ?r ? s и ?(r ? s); 3) ?m ? ?n и ?(m ? n). Наличие в каждой паре общих переменных позволяет сопоставлять их по смыслу и устанавливать истинность отношения.

Сложные сравнимые суждения могут быть совместимыми и несовместимыми.

Отношение совместимости

К совместимым относятся такие сравнимые суждения, которые одновременно могут быть истинными. В сложных суждениях, как и в простых, различают три вида совместимости: эквивалентность, частичная совместимость и подчинение.

1. Эквивалентные — это суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными.

В таблице 8 показано эквивалентное отношение между сложными суждениями. А и В — схемы суждений; знак ? — отношение эквивалентности для сложных суждений.

Таблица 8

Таблица 9

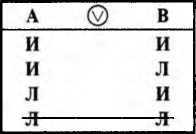
Таблица 10

1-я и 4-я строки таблицы показывают, что А и В одновременно принимают одинаковые значения — И и Л; зачеркнутые 2-я и 3-я строки показывают, что эквивалентные суждения одновременно не могут принимать различные значения.

Отношение эквивалентности позволяет выражать одни сложные суждения через другие — конъюнкцию через дизъюнкцию или импликацию и наоборот. Приведем четыре известные эквивалентности, которые являются законами логики.

1) Выражение конъюнкции через дизъюнкцию:

?(A ? B) ? ?A ? ?B

2) Выражение дизъюнкции через конъюнкцию:

?(A ? B) ? ?A ? ?B

Эти две эквивалентности называются законами де Моргана.

3) Выражение импликации через конъюнкцию:

?(A ? B) ? (A ? ?B)

4) Выражение импликации через дизъюнкцию:

A ? B ? ?A ? B

2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

Отношение частичной совместимости для сложных суждений показано в таблице 9, где А и В — схемы сложных суждений; ? — знак частичной совместимости. 1-я строка таблицы говорит об одновременной истинности А и В; 2-я и 3-я — несовпадение значений; 4-я строка зачеркнута, поскольку исключается одновременная ложность А и В.

3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным.

В таблице 10 показано отношение подчинения между сложными суждениями: А и В — схемы суждений; ? — знак подчинения. 1-я строка показывает, что в случае истинности А истинным является и В. В 3-й и 4-й строках А является ложным, а В принимает произвольные значения. 2-я строка в таблице зачеркнута, поскольку отношение подчинения исключает ложность подчиненного В при истинности подчиняющего А.

Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующею все виды рассуждений.

Отношение несовместимости

Несовместимыми являются суждения, которые одновременно не могут быть истинными. Это противоположность и противоречие.

1. Противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.

В таблице 11 показано отношение противоположности между суждениями: А и В — схемы суждений; ? — знак логической противоположности. 1-я строка таблицы зачеркнута. Это означает, что оба суждения одновременно не могут быть истинными; 2-я и 3-я строки показывают, что суждения могут принимать исключающие значения; 4-я строка — оба суждения могут быть ложными. Это значит, что при ложности одного из противоположных суждений нельзя установить значения другого: оно может быть как истинным, так и ложным.

2. Противоречие — отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое ложно, а при ложности первого второе истинно.

Противоречащие отношения между сложными суждениями показаны в таблице 12; А и В — схемы сложных суждений, ? — знак отношения противоречия.

Таблица 11

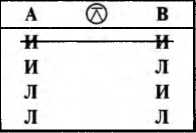
Таблица 12

Вычеркнутые 1-я и 4-я строки показывают, что А и В могут принимать лишь альтернативные значения.

Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию. Так, например, для р противоречащим будет ?р; для конъюнкции р ? q противоречием будет ее отрицание — ?(р ? q) и т. п.

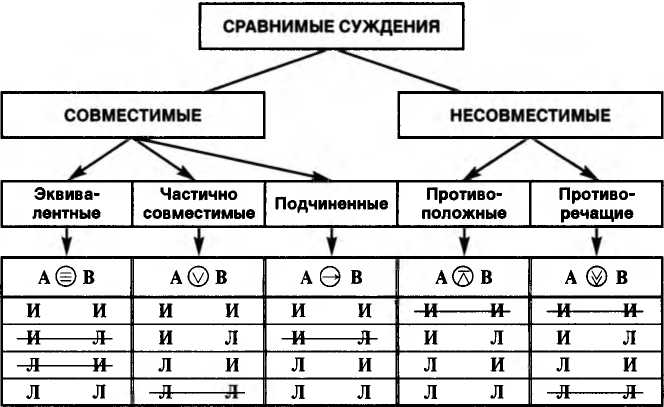
Обобщенная таблица логических отношений между сложными суждениями (таблица 13).

Таблица 13

Сопоставление суждений в дискуссиях

Отчетливое представление об отношениях, в которых могут находиться суждения, позволяет логически грамотно анализировать высказывания участников дискуссий. Бывают ситуации, когда логический анализ показывает совместимость различных по структуре суждений. Нередко это случается с частными суждениями. Пропонент утверждает, что «Некоторые S есть Р»; оппонент настаивает, что «Некоторые S не есть Р». На поверку же выходит, что эти суждения не исключают друг друга, а являются частично совместимыми и оба могут оказаться истинными.

В спорах и дискуссиях могут смешиваться противоречащие и противоположные суждения. Например, обвинитель утверждает, что в рассматриваемом случае имело место убийство (р), которое совершено умышленно (q). Защитник не отрицает факта убийства (р), но считает, что оно было совершено без умысла (?q). Каждый из них считает, что эти утверждения — (р ? q) и (р ? ?q) исключают друг друга как альтернативные. В действительности же оказывается, что эти высказывания находятся в отношении противоположности.

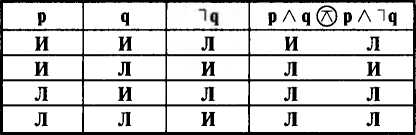
В этом легко убедиться с помощью таблицы 14. Анализ показывает, что эти высказывания несовместимы, поскольку ни в одной строке не являются одновременно истинными. Вместе с тем они могут быть ложными (3-я и 4-я строки), значит, находятся в отношении противоположности. Отсюда следует, что если будет показана в целом несостоятельность утверждения обвинителя, то это еще не означает правоту защитника. Точно так же опровержение утверждений защитника логически не обязывает принимать точку зрения обвинителя. Может оказаться, что оба утверждения ложны и задача сведется к поиску нового объяснения фактам.

Таблица 14

Вопросы для самопроверки

1. Какие сложные суждения являются несравнимыми и какие — сравнимыми?

2. На какие виды делятся сравнимые суждения?

3. На какие виды совместимости делятся сложные суждения?

4. Какие значения принимают эквивалентные отношения совместимости и несовместимости?

Данный текст является ознакомительным фрагментом.