Правило XVIII

Правило XVIII

Для этого требуются только четыре действия: сложение, вычитание, умножение и деление; два последних здесь зачастую не следует производить, как для того, чтобы невзначай не запутать чего-нибудь, так и потому, что впоследствии они могут быть выполнены более легко.

Многочисленность правил часто проистекает из неопытности учителя, и то, что могло бы быть сведено к единому общему предписанию, становится менее очевидным, если разделяется на многие частности. Вот почему все действия, которыми нужно пользоваться при рассмотрении вопросов, т. е. при выведении каких-то величин из других, мы сводим здесь лишь к четырем главным; то, каким образом они оказываются достаточными, познается из их объяснения.

А именно, если мы приходим к познанию одной величины благодаря тому, что мы знаем части, из которых она составлена, это делается посредством сложения; если мы узнаём часть благодаря тому, что знаем целое и превышение целого над той же самой частью, это делается посредством вычитания; и какая-либо величина не может быть большим числом способов выведена из других, взятых в абсолютном смысле, величин, в которых она определенным образом содержится. Если же какая-либо величина должна быть найдена на основании других, от которых она совершенно отлична и в которых она никоим образом не содержится, необходимо соотнести ее с ними каким-нибудь способом; и когда это отношение, или соответствие, нужно обозреть прямо, тогда следует пользоваться умножением, когда косвенно — делением.

Чтобы ясно описать два последних действия, надо знать, что единица, о которой мы уже говорили, является здесь основанием и фундаментом всех отношений и в ряде непрерывно пропорциональных величин она занимает первую ступень, данные же величины содержатся на второй ступени, а искомые — на третьей, четвертой и остальных, если соотношение прямое, если же оно косвенное, искомая величина содержится на второй и других промежуточных ступенях, а данная — на последней.

Действительно, когда говорится, что, как единица относится к а, или к данному числу 5, так b, или данное число 7, относится к искомому, которое равно ab, или 35, тогда а и Ь находятся на второй ступени, и ab, являющееся их произведением, — на третьей. Равным образом, когда добавляют, что, как единица относится к с, или 9, так ab, или 35, относится к искомому аbс, или 315, тогда abc находится на четвертой ступени и получается посредством двух действий умножения ab на с, т. е. величин, находящихся на второй ступени, и т. д. Равным образом, как единица относится к а, (или) 5, так а, (или) 5, относится к а², или 25; и опять-таки как единица относится к (а, или) 5, так а², (или) 25, относится к а³, (или) 125; и, наконец, как единица относится к а, (или) 5, так а³, (или) 125, относится к а⁴, т. е. к 625, и т. д.: ведь когда одна и та же величина умножается на саму себя, умножение производится так же, как и тогда, когда она умножается на другую, совершенно отличную от нее величину.

Когда же теперь говорится, что, как единица относится к а, или 5, данному делителю, так В, или искомое число 7, относится к ab, или 35, данному делимому, тогда порядок является обратным и косвенным, вследствие чего искомое В не может быть получено иначе, кроме как посредством деления данного ab на а, также данное. Равным образом, когда говорится, что, как единица относится к А, или искомому числу 5, так А, или 5, искомое, относится к а², или 25, данному; или же как единица относится к А, (или) 5, искомому, так А², или 25, искомое, относится к а³, или 125, данному, и т. д. Все это мы охватываем названием «деление», хотя следует отметить, что последние из примеров такого вида заключают в себе большее затруднение, чем первые, ибо в них чаще встречается искомая величина, которая поэтому предполагает многие отношения. Ведь смысл этих примеров тот же самый, как если бы было сказано, что надо извлечь квадратный корень из а, или <из> 25, либо кубический из а³, или из 125, и т. д.; такой способ выражения употребителен у счетчиков. Или, если объяснить их также в терминах геометров, это то же самое, как если бы было сказано, что надо найти среднюю пропорциональную между той принятой величиной, которую мы называем единицей, и той, которая обозначается а², либо две средние пропорциональные между единицей и а³, и т. д.

Из этого легко сделать вывод о том, каким образом двух названных действий достаточно для отыскания любых величин, которые должны быть выведены из других величин благодаря какому-либо отношению. После того как мы поняли это, нам следует изложить, каким образом эти действия должны быть рассмотрены воображением и каким образом они должны также предстать перед глазами, для того чтобы затем мы наконец объяснили их использование, или применение.

Если нужно произвести сложение или вычитание, мы представляем себе предмет в виде линии или в виде протяженной величины, в которой должна быть рассмотрена только длина: действительно, если нужно прибавить линию

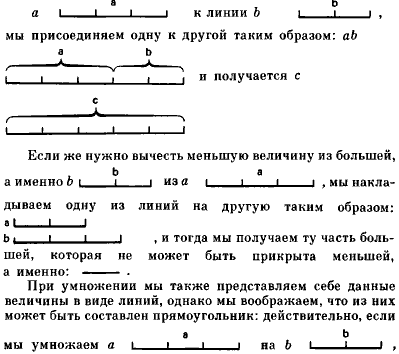
мы прикладываем одну линию к другой под прямым углом таким образом:

и получается прямоугольник

Наконец, при делении, в котором дан делитель, мы воображаем, что делимая величина представляет собой прямоугольник, одна сторона которого является делителем, а другая — частным; так, если прямоугольник ab нужно разделить на а,

из него убирают ширину а, и остается b в качестве частного: . Или, наоборот, если тот же прямоугольник делят на b, то убирают высоту b, и а будет частным: .

Что же касается тех делений, в которых делитель не дан, а только обозначен через посредство какого-либо отношения, как, например, когда говорится, что нужно извлечь квадратный или кубический корень и т. д., то следует отметить, что в этих случаях и подлежащий делению, и все другие термины нужно всегда представлять себе как линии, расположенные в ряде непрерывно пропорциональных величин, первой из которых является единица, а последней — делимая величина. О том, каким образом между этой величиной и единицей должно быть найдено сколько угодно средних пропорциональных, будет сказано в своем месте. Теперь же достаточно уведомить, что здесь, как мы предполагаем, подобные действия еще не были доведены до совершенства, так как они должны производиться при посредстве непрямых и обратных актов воображения, а сейчас мы говорим только о вопросах, которые следует обозревать прямо.

Что касается других действий, то они, конечно, весьма легко могут быть осуществлены тем способом, которым, как мы сказали, их надлежит понимать. Вместе с тем остается изложить, каким образом должны быть подготовлены используемые в них термины; ибо, хотя, впервые занимаясь каким-либо затруднением, мы вольны представлять себе его термины как линии или как прямоугольники и никогда не приписывать этим терминам других фигур, как было сказано в четырнадцатом правиле, тем не менее в рассуждении часто бывает, что прямоугольник, после того как он был образован умножением двух линий, затем следует представлять себе в виде линии, для того чтобы выполнить другое действие, либо тот же самый прямоугольник или линию, полученную в результате какого-то сложения или вычитания, затем следует представлять себе как некоторый другой прямоугольник, построенный на обозначенной линии, которой он должен быть разделен.

Итак, здесь стоит изложить, каким образом всякий прямоугольник можно преобразовать в линию и в свою очередь линию или даже прямоугольник — в другой прямоугольник, сторона которого обозначена. Это весьма легко сделать геометрам, если только они заметят, что в виде линий, всякий раз когда мы, как здесь, сравниваем их с каким-либо прямоугольником, мы неизменно представляем себе прямоугольники, одна сторона которых является той длиной, какую мы приняли за единицу. Ведь тогда вся эта задача сводится к положению такого вида: по данному прямоугольнику построить другой, равный ему, на данной стороне.

Хотя это действие известно даже новичкам в геометрии, тем не менее мне хочется объяснить его, чтобы не показалось, будто я что-либо упустил.