Правило XVI

Правило XVI

Что же касается вещей, которые не требуют наличного внимания ума, хотя и необходимы для заключения, то их лучше обозначать посредством наиболее сокращенных знаков, чем посредством полных фигур, ибо тогда память не сможет ошибаться, а вместе с тем и мысль не будет отвлекаться на то, чтобы удержать их, в то время как она занята выведением других.

Впрочем, поскольку мы сказали, что из бесчисленных измерений, которые могут быть изображены в нашей фантазии, нужно созерцать одним взором глаз или ума не более двух различных измерений, то важно удерживать в памяти все остальные таким образом, чтобы они легко представлялись всякий раз, когда потребует необходимость; по-видимому, с этой целью память и была создана природой. Но так как память зачастую подвержена ошибкам, то для того, чтобы мы не были вынуждены уделять некоторую часть нашего внимания ее восстановлению, в то время когда мы заняты другими мыслями, искусство весьма кстати открыло возможность применения письменности. Полагаясь на ее помощь, мы здесь совершенно ничего не вверяем памяти, но, предоставив свободной фантазии в целом наличные идеи, изображаем на бумаге все, что должно быть сохранено, и делаем это посредством наиболее сокращенных знаков, чтобы, после того как в соответствии с девятым правилом мы рассмотрели каждый из них в отдельности, мы смогли в соответствии с одиннадцатым правилом обозреть их все в наибыстрейшем движении мысли и одновременно охватить взором наибольшее их число.

Итак, все, что для разрешения затруднения надлежит рассматривать как нечто единое, мы будем обозначать одним знаком, который может быть изображен как угодно. Но ради удобства мы воспользуемся буквами а, b, с и т. д. для выражения уже известных величин и А, В, С и т. д. для выражения неизвестных. Мы часто будем ставить перед ними цифры 2, 3, 4, и т. д. для того, чтобы обозначить количество этих величин; вместе с тем мы будем располагать цифры и позади них, для того чтобы обозначать число отношений, которые надлежит в них уразуметь: так, если я напишу 2а³, это будет то же самое, как если бы я сказал: удвоение величины, обозначаемой буквой а и содержащей три отношения. И благодаря этому приему мы не только произведем сокращение многих выражений, но и, что особенно важно, представим термины затруднения в столь чистом и подлинном виде, что, не упуская ничего полезного, мы вместе с тем никогда не найдем в них ничего излишнего и того, что напрасно отвлечет способности ума, в то время как нужно будет одновременно охватить умом многие вещи.

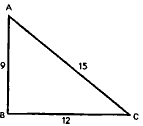
Для того чтобы яснее уразуметь все это, нужно прежде всего заметить, что счетчики имели обыкновение обозначать каждую из величин посредством многих единиц или посредством какого-либо числа, мы же в данном случае отвлекаемся от самих чисел не меньше, чем несколько ранее от геометрических фигур или от любой другой вещи. Мы делаем это как для того, чтобы избежать пресыщения долгим и ненужным вычислением, так и в особенности для того, чтобы части предмета, которые имеют отношение к природе затруднения, всегда оставались раздельными и не скрывались за бесполезными числами: например, если отыскивается основание прямоугольного треугольника, данные стороны которого равняются 9 и 12, счетчик скажет, что оно равно ?225, или 15; мы же вместо 9 и 12 поставим а и b и найдем, что основание равно ?(а² + b²), при этом те два члена а² и b², которые в числе являются слитыми, останутся раздельными.

Нужно также заметить, что под числом отношений надлежит понимать следующие в непрерывном порядке пропорции, которые в общепринятой алгебре иные пытаются выразить посредством многих измерений и фигур; первую из них они называют корнем, вторую — квадратом, третью — кубом, четвертую — биквадратом и т. д. Признаюсь, что эти названия долгое время вводили меня самого в заблуждение, ибо мне казалось, что после линии и квадрата моему воображению ничто не может представиться яснее, чем куб и другие фигуры, созданные по их подобию; и действительно, с помощью этих фигур я разрешил немало затруднений. Однако в конце концов после многих опытов я убедился в том, что никогда не находил благодаря этому способу понимания ничего такого, чего я не сумел бы познать гораздо легче и отчетливее и без него, а также в том, что нужно полностью отбросить такие названия, чтобы не извратить ими наше представление, ибо одна и та же величина, хотя она и называется кубом или биквадратом, тем не менее, согласно предшествующему правилу, никогда не должна представляться воображению иначе как в виде линии или поверхности. Поэтому нужно особо отметить, что корень, квадрат, куб и т. д. являются не чем иным, как непрерывно пропорциональными величинами, которым, как предполагается, всегда предпослана та принятая единица, о коей мы уже говорили выше. Первая пропорциональная величина связана с этой единицей непосредственно и одним лишь отношением, вторая же связана с ней через посредство первой и потому — двумя отношениями, третья — через посредство первой и второй и тремя отношениями и т. д. Итак, отныне мы будем называть первой пропорциональной ту величину, которая в алгебре именуется корнем, второй пропорциональной — ту, которая именуется квадратом, и т. д.

Наконец, нужно заметить, что, хотя мы отвлекаем здесь термины затруднения от некоторых чисел для того, чтобы исследовать его природу, тем не менее часто бывает так, что оно может быть разрешено более простым способом с помощью данных чисел, чем если бы оно было отвлечено от них: это происходит благодаря двойному применению чисел (которого мы уже коснулись ранее), а именно потому, что одни и те же числа раскрывают то порядок, то меру. И стало быть, после того как мы исследовали это затруднение, выраженное в общих терминах, нужно свести его к данным числам, чтобы увидеть, не наведут ли они нас тогда, быть может, на какое-то более простое решение: например, после того как мы увидели, что основание прямоугольного треугольника со сторонами а и b равно ?(a² + b²) и что вместо а² надо поставить 81, а вместо b² — 144, т. е. числа, дающие в сумме число 225, корень которого, или средняя пропорциональная между единицей и 225, равен 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому, что оно вообще является основанием прямоугольного треугольника, одна сторона которого относится к другой, как 3 к 4. Все это различаем мы, стараясь обрести очевидное и отчетливое познание вещей, а не счетчики, которые, когда им попадается искомая сумма, бывают удовлетворены, даже если они не замечают, каким образом она зависит от данных чисел; однако только в этом, собственно, и заключается наука.

Вообще же следует заметить, что никогда не нужно вверять памяти какую-либо из тех вещей, которые не требуют постоянного внимания, если мы можем изложить их на бумаге, а именно для того, чтобы бесполезным воспоминанием не отвлекать какую-то часть нашего ума от познания наличного объекта. И надо составить таблицу, в которую мы запишем термины вопроса в том виде, в каком они будут изначально представлены, а затем то, каким образом они отвлекаются и посредством каких знаков выражаются, чтобы, после того как решение будет найдено в этих самых знаках, мы легко и без всякой помощи памяти применили его к частному предмету, о котором будет стоять вопрос; действительно, никогда нельзя отвлекать что-либо, кроме как от чего-то менее общего. Итак, я пишу следующим образом: в прямоугольном треугольнике ABC отыскивается основание АС, — и представляю затруднение в отвлеченном виде, чтобы вообще отыскивалась величина основания по величинам сторон; затем вместо стороны АВ, которая равна 9, я ставлю а, вместо стороны ВС, которая равна 12, я ставлю b, и т. д.

Необходимо отметить, что мы еще воспользуемся этими четырьмя правилами в третьей части настоящего трактата и будем понимать их несколько шире, чем они были истолкованы здесь, так, как будет сказано в своем месте.