Вопросы и задания к главе 1
Вопросы и задания к главе 1
1. Что такое логика? Чем она отличается от многих наук, которые занимаются мышлением? Что такое содержание и форма мышления? Почему логика часто называется формальной логикой? Какие существуют формы мышления? Приведите несколько примеров понятий, суждений и умозаключений. Что такое законы логики? Какую роль они играют в нашем мышлении? Что такое софизмы?
2. Когда и где появилась логика? Кто считается ее создателем? Что такое традиционная логика? Когда появилась символическая, или математическая логика? Какие идеи лежат в ее основе? Чем отличается традиционная логика от символической, и в чем заключается их сходство? Являются ли традиционная логика и символическая логика различными науками? Что называется «исчислениями» в символической логике?
3. Как вы думаете, зачем нужна человеку логика? Какую роль она играет в его жизни? Можно ли, на ваш взгляд, без нее обойтись? Что такое интуитивная логика? Попытайтесь привести примеры, иллюстрирующие тот факт, что даже никогда не изучавшие логику люди все равно интуитивно ей пользуются.
4. Что такое понятие? Как соотносятся понятие и слово? Можно ли утверждать, что понятие и слово – это одно и то же? Что такое содержание и объем понятия? Как они соотносятся? Что представляет собой принцип обратного отношения между содержанием и объемом понятия? Приведите примеры понятий, иллюстрирующие этот принцип.
5. Какими бывают понятия по объему и содержанию? Приведите по 10 примеров для понятий единичных, общих, нулевых, собирательных, несобирательных, конкретных, абстрактных, положительных, отрицательных. Что такое логическая характеристика понятия? Как она составляется? Какие ошибки часто допускаются при составлении логической характеристики понятий?
6. Дайте логическую характеристику следующим понятиям: 1. Луна, 2. растение, 3. столица государства, 4. музыкальный коллектив, 5. знаменитый художник, 6. кентавр, 7. датский физик Нильс Бор, 8. древний философ, 9. Антарктида, 10. Атлантида, 11. сборная России, 12. лист бумаги, 13. молекула воды, 14. преступное сообщество, 15. уровень преступности, 16. невежество, 17. глупость, 18. умный человек, 19. драгоценный камень, 20. пьяная компания, 21. неправда, 22. водород, 23. геометрия, 24. рота солдат, 25. несправедливость, 26. эксплуатация, 27. воздух, 28. философы милетской школы, 29. знаменитое произведение искусства, 30. тишина.
7. Придумайте понятия, соответствующие следующим логическим характеристикам:
а) общее, несобирательное, конкретное, положительное.
б) единичное, несобирательное, конкретное, положительное.
в) единичное, собирательное, конкретное, положительное.
г) общее, собирательное, конкретное, положительное.
д) общее, несобирательное, абстрактное, отрицательное.
е) нулевое, несобирательное, абстрактное, положительное.
ж) нулевое, собирательное, конкретное, положительное.
з) общее, собирательное, конкретное, отрицательное.
е) единичное, несобирательное, абстрактное, положительное.
и) нулевое, несобирательное, конкретное, отрицательное.
8. Что такое определенное понятие? В каком случае можно говорить, что понятие имеет ясное содержание и резкий объем? Что представляют собой неопределенные понятия? Объясните, что такое неясное содержание и нерезкий объем понятия? Каковы основные причины появления и существования неопределенных понятий? Можно ли без них обойтись, вообще исключив их из мышления и языка? Если невозможно, то почему?
9. Представляют ли неопределенные понятия сами по себе, вне зависимости от ситуации, в которой они употребляются, коммуникативные помехи? Почему, на ваш взгляд, употребление неопределенных понятий в повседневном общении не приводит нас к коммуникативным затруднениям? В каких случаях неопределенные понятия могут стать причиной различных затруднений и сыграть негативную роль? Каким образом возможно бороться с ними в этих ситуациях?
10. Почему процедура превращения неопределенного понятия в определенное всегда условна и относительна, в силу чего неопределенное понятие, в конечном итоге, остается неопределенным?
Приведите по десять примеров для определенных и неопределенных понятий.
11. Какие из следующих понятий являются определенными, а какие неопределенными: 1. карась, 2. млекопитающее животное, 3. большая собака, 4. дикая кошка, 5. престижное учебное заведение, 6. московское учебное заведение, 7.планета Нептун, 8. яркая звезда, 9. талантливый человек, 10. богач, 11. бездарный преподаватель, 12. кандидат физико-математических наук, 13. хулиган, 14. известный писатель,
15. высокие горы, 16. учебник по химии, 17. хорошая музыка, 18. скучная лекция, 19. добротная одежда, 20. скромная пища, 21. сборная России по футболу, 22. крупный город, 23. столица государства?
12. Путем прибавления к содержанию следующих понятий каких-либо признаков превратите их из неопределенных в условно-определенные: высокий человек, старик, богач, лысый, толстая книга, современная музыка, плохая погода, высокая зарплата, хорошие соседи, двоечник, известный писатель, крупное военное сражение, большой стадион, плохой учитель, несвежие продукты, редкая удача, безрассудный поступок.
13. Что такое сравнимые и несравнимые понятия? Приведите по пять примеров для сравнимых и несравнимых понятий. Какие понятия называются в логике совместимыми, а какие – несовместимыми? Приведите по пять примеров для совместимых и несовместимых понятий.
14. В каких отношениях могут быть совместимые понятия? Что представляют собой отношения равнозначности, пересечения и подчинения между понятиями? Что такое видовые и родовые понятия? В каких отношениях могут быть несовместимые понятия? Что представляют собой отношения соподчинения, противоположности и противоречия между понятиями? Чем отличается противоположность от соподчинения и противоречие от противоположности?
15. Каким образом изображаются отношения между понятиями? В каком отношении находятся понятия, обозначающие часть и целое? Почему между этими понятиями не может быть отношения подчинения?
Почему возможно утверждать, что несравнимые понятия находятся в отношении соподчинения? Приведите пять примеров несравнимых понятий для иллюстрации своего ответа, прокомментировав каждый из них.
16. Почему невозможно точно установить отношения между неопределенными понятиями? Приведите примеры, иллюстрирующие ваш ответ. Приведите по три примера для каждого случая отношений между понятиями: равнозначности, пересечения, подчинения, соподчинения, противоположности и противоречия.
17. В каких отношениях находятся следующие понятия: 1. двоечник и студент, 2. композитор и человек, 3. город и деревня, 4. Антарктида и ледовый материк, 5. небесное тело и звезда, 6. треугольник и сторона треугольника, 7. школа № 5 и учебное заведение, 8. майор и россиянин, 9. знаменитый человек и немецкий писатель, 10. дом и крыша дома, 11. собака и кошка, 12. умный человек и неумный человек, 13. монарх и самодержец, 14. физика и химия, 15. геометрия и тригонометрия, 16. столица и населенный пункт, 17. книга и интересная книга, 18. телевизор и планета солнечной системы, 19. растение и крапива, 20. окружность и круг, 21. Николай II и последний русский царь, 22. олимпийские игры и спортивные состязания?
18. С помощью круговых схем Эйлера изобразите отношения между следующими группами понятий:
19. Подберите понятия, соответствующие следующим схемам:
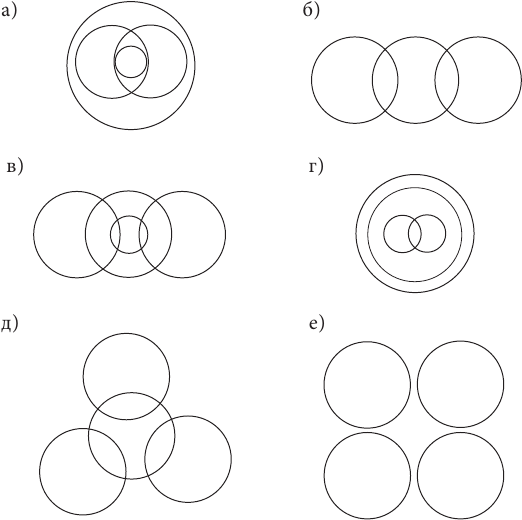
20. Что такое ограничение понятия? Почему для уменьшения объема понятия надо прибавлять какие-либо признаки к его содержанию? Что представляет собой логическая операция обобщения понятия? Каким образом ограничения и обобщения понятий складываются в логические цепочки? Каковы пределы цепочек ограничений и обобщений?
21. Какие ошибки часто допускают при ограничении и обобщении понятий? Продемонстрируйте на самостоятельно подобранных примерах, что целое и часть нельзя путать с видом и родом. Всякое ли понятие можно подвергнуть ограничению и обобщению? Какие понятия не поддаются этим логическим операциям?
22. Подберите десять любых понятий и сделайте с каждым из них ограничение и обобщение, т. е. подберите для каждого из них как видовое, так и родовое понятие, иллюстрируя эти операции круговыми схемами Эйлера. Возьмите какое-либо понятие и постройте логическую цепочку его ограничения до предела. Возьмите какое-либо понятие и постройте цепочку его обобщения до предела.
23. Совершите ограничение и обобщение со следующими понятиями: 1. школа, 2. знаменитый писатель, 3. математическое действие, 4. картина, 5. предмет мебели, 6. университет, 7. планета, 8. американский президент, 9. актер, 10. химический элемент, 11. древнегреческий ученый, 12. балет, 13. уровень преступности, 14. музей, историческое событие, 15. яблоня, 16. всемирно известный спортсмен, 17. материк, 18. книга, 19. хищник, 20. высотное здание, 21. молодой человек, 22. музыкальный коллектив, 23. сборная России, 24. ураган, 25. электричество, 26. стихотворение.
24. Какие из приведенных ниже понятий невозможно подвергнуть ограничению или обобщению: 1. тетрадь, 2. МГУ, 3. галактика, 4. русский писатель XIX века, 5. первый космонавт земли, 6. Вселенная, 7. химический элемент, 8. Россия, 9. древнее государство, 10. Солнце, 11. современный автомобиль, 12. млекопитающее животное, 13. небоскреб, 14. атомная электростанция, 15. столица Франции, 16. нечто существующее, 17. планета Юпитер, 18. Третьяковская галерея, 19. московский кинотеатр, 20. толстая книга, 21. бытие?
25. Что представляет собой логическая операция определения понятия? Чем отличаются явные определения от неявных? Придумайте по три примера явных и неявных определений. Что такое реальные и номинальные определения? Как вы думаете, почему возможно утверждать, что любое реальное определение можно свести к номинальному и наоборот?
26. Что представляет собой классический способ определения понятия? Дайте определения каким-нибудь трем понятиям, пользуясь классическим способом определения. Каковы основные правила определения понятия? Какие ошибки возникают при их нарушении? Приведите, подобрав самостоятельно, по три примера для каждой ошибки в определении понятия.
27. Допущены ли ошибки в определениях, приведенных ниже? Если допущены, то какие?
а) Фильтрование – это процесс разделения какого-либо вещества с помощью специального приспособления – фильтра.
б) Кость – это орган, обладающий сложным строением.
в) Бескорыстие – это отсутствие личной заинтересованности при оказании какой-либо помощи.
г) Гравитация – это явление, которое выражается во взаимодействии двух физических тел.
д) Барометр – это метеорологический измерительный прибор.
е) Математика – это гимнастика ума.
ж) Сверхпроводник – это вещество, обнаруживающее явление сверхпроводимости.
з) Логика – это наука о формах и законах правильного мышления.
и) Извлечение квадратного корня – это математическое действие, которое не является ни умножением, ни делением, ни возведением в степень.
28. Что представляет собой логическая операция деления понятия? Чем она отличается от операции определения? Какова структура деления? Что такое основание деления? Какое деление называется дихотомическим? Попробуйте отметить достоинства и недостатки дихотомического деления. Какую роль в научном и повседневном мышлении играет логическая операция деления понятия?
29. Каковы основные логические правила деления понятия? Какие ошибки возникают при их нарушении? Придумайте по три примера для каждой ошибки в делении понятия. Почему дихотомическое деление понятия всегда является безошибочным? Каким образом оно исключает все возможные в делении ошибки?
30. Допущены ли ошибки в приведенных ниже примерах деления? Если допущены, то какие?
а) Воды земного шара бывают пресными и солеными.
б) Учащиеся бывают успевающими, отстающими и отличниками.
в) Речь бывает устной, письменной, путанной и заумной.
г) Спортивные состязания бывают мировыми, международными, олимпийскими и другими.
д) Треугольники бывают тупоугольными и прямоугольными.
е) Жиры бывают растительными, животными и твердыми.
ж) Люди бывают высокими и невысокими.
з) Оружие бывает холодным, огнестрельным и старинным. и) Высшие учебные заведения делятся на университеты, институты, академии и высшие училища.
31. Что представляют собой логические операции сложения и умножения понятий? Что такое логическая сумма и логическое произведение? Возьмите три пары каких-нибудь понятий и сделайте с ними логические операции сложения и умножения, иллюстрируя их результаты с помощью круговых схем Эйлера.
32. Каковы результаты сложения и умножения понятий во всех случаях отношений между ними? Могут ли эти результаты полностью совпадать? Может ли логическая сумма или логическое произведение быть нулевым понятием?
33. Какие союзы естественного языка являются, как правило, выражением результатов сложения и умножения понятий? Проиллюстрируйте свой ответ самостоятельно подобранными примерами. В чем заключается неоднозначность употребления союза или как показателя логического сложения понятий?
34. Произведите сложение и умножение следующих понятий, изобразив результаты этих операций с помощью круговых схем Эйлера: 1. майор и военнослужащий, 2. атом и молекула, 3. квадрат и ромб с прямым углом, 4. известный актер и россиянин, 5. млекопитающее животное и лошадь.
Данный текст является ознакомительным фрагментом.