ГЛАВА XIX: Искусственный Интеллект: виды на будущее

ГЛАВА XIX: Искусственный Интеллект: виды на будущее

Ситуации «почти» и ситуации гипотетические

ПРОЧИТАВ «КОНТРАФАКТУС», один из моих друзей сказал мне: «Мой дядя был почти президентом США!» «Правда?» — спросил я. «Конечно», — ответил он, — «он был капитаном торпедного катера ПТ108». (Джон Ф. Кеннеди был капитаном ПТ109.)

Именно об этом идет речь в «Контрафактусе». У нас в голове каждый день рождаются мысленные варианты ситуаций, с которыми нам приходится сталкиваться, идей, которые у нас возникают или событий, происходящих вокруг. При этом некоторые детали остаются без изменений, в то время как другие «сдвигаются». Какие детали мы сдвигаем? Какие нам даже в голову не приходит изменить? Какие события воспринимаются нами на некоем глубинном интуитивном уровне как близкие родственники событий, случившихся на самом деле? Что мы считаем «почти» случившимся, чем-то, что «могло» случиться, хотя совершенно точно знаем, что в действительности этого не произошло? Какие альтернативные версии событий сами собой возникают у нас в мозгу, когда мы слышим какой-нибудь рассказ? Почему одни контрафактические ситуации кажутся нам менее «контрафактическими», чем другие? В конце концов, совершенно ясно, что чего не было, того не было. У «неслучаемости» нет никаких степеней. То же самое верно и в отношении «почти» случившихся ситуаций. Мы часто жалуемся, что какое-то событие «чуть не случилось»; не менее часто мы произносим те же слова с облегчением. Но это «чуть не» находится в нашем мозгу, а не во внешних фактах.

Вы едете на машине по проселочной дороге и внезапно перед вами появляется рой пчел. Вместо того, чтобы беспристрастно отметить происходящее, ваш мозг тут же создает целый рой «повторов». Как правило, вы думаете что-то вроде: «Хорошо, что окошко было закрыто!» — или же: «Ах, черт, если бы только окошко было закрыто…» «Хорошо, что я не на велосипеде!» «Лучше бы я проехал здесь на пять секунд раньше.» Странными, но возможными повторами были бы: «Если бы это был олень, я мог бы быть сейчас мертв!» или «Могу поспорить, что эти пчелы предпочли бы столкнуться с розовым кустом!» А вот повторы еще страннее: «Жаль, что это были пчелы, а не долларовые купюры!» «Хорошо, что пчелы не цементные!» «Лучше бы это была всего одна пчела, вместо целого роя.» «Не хотел бы я оказаться на месте этих пчел!» Какие сдвиги кажутся нам естественными, а какие нет — и почему?

В недавнем номере журнала «Нью-Йоркер» был перепечатан следующий отрывок из «Филадельфия Уэлкомат»:[81]

Если бы Леонардо да Винчи родился женщиной, потолок Сикстинской капеллы мог бы никогда не быть расписан. А если бы Микеланджело был сиамскими близнецами, то работа могла бы оказаться законченной вдвое быстрее.

Смысл этого замечания не в том, что подобные гипотетические ситуации ложны, а в том, что люди, которым может придти в голову «сдвинуть» пол или число данного человека, должны быть не совсем нормальными. Интересно то, что в том же номере, ничтоже сумняшеся, напечатали следующую фразу, завершающую обзор книги:

Я думаю, что ему (профессору Филиппу Франку) очень понравились бы обе эти книги.[82]

Однако бедный профессор Франк уже умер; ясно, что бессмысленно предполагать, что кто-то может прочитать книги, изданные после его смерти. Почему же эта фраза воспринимается нами всерьез? Дело в том, что в каком-то трудноуловимом смысле сдвиг параметров в этом случае не нарушает нашего чувства «возможного» так сильно, как в предыдущих примерах. Что-то здесь позволяет нам вообразить легче, чем в других случаях, что «при прочих равных» меняется именно этот параметр. Но почему? Каким образом наша классификация событий и людей позволяет нам на каком-то глубоком уровне определять, что может быть сдвинуто без проблем и что не подлежит сдвигу?

Посмотрите, насколько естественным кажется нам переход от скучного утверждения «Я не знаю английского» к более интересному сослагательному наклонению «Я бы хотел знать английский» и, наконец, к богатому смыслом гипотетическому «Если бы я знал английский, я бы читал Диккенса и Шекспира в оригинале». Насколько плоским и мертвым был бы разум, для которого отрицание являлось бы непроницаемым барьером! Живой разум всегда способен увидеть окно в мир возможностей.

Мне кажется, что гипотетические «почти» ситуации и бессознательно вырабатываемые возможные миры представляют из себя один из богатейших источников информации о том, каким образом люди организуют и классифицируют свои впечатления о мире. Красноречивый сторонник подобного взгляда, лингвист и переводчик Джон Штейнер написал в своей книге «После Вавилонского столпотворения»:

Гипотетические ситуации, воображаемые условия, синтаксис контрафактического и случайного вполне могут быть порождающим центром человеческого языка… (Они) не просто придают речи философскую и грамматическую сложность. Не менее, чем будущие времена, с которыми, как мы чувствуем, они тесно связаны и вместе с которыми, возможно, должны быть отнесены к более широкой категории предположительных или альтернативных событий, «если бы» предложения лежат в основе динамики человеческих чувств…

Мы отличаемся умением и необходимостью отрицать и переигрывать реальные ситуации, воображать и выражать мир иначе.... Нам нужно какое-то слово, которое обозначало бы эту возможность языка, это стремление к выражению «иначести». … Может быть, слово «альтерность» подошло бы для определения ситуаций, отличных от данной, — контрафактических высказываний и миров, куда нас уводит наше воображение, образов, которыми мы населяем свою голову и с помощью которых создаем изменчивую и часто фиктивную среду своего физического и общественного существования.

В завершение, Штейнер поет контрафактический гимн контрафактичности:

Маловероятно, что человек, существовал бы таким, каким мы его знаем, если бы в языке не было фиктивных, контрафактических, анти-детерминистских оборотов, если бы он не обладал семантической способностью, рожденной и сохраняющейся в «лишних» областях коры мозга, — способностью представлять и выражать возможности, лежащие за пределами органического разложения и смерти.[83]

Создание «гипотетических миров» происходит настолько случайно и естественно, что мы почти не отдаем себе отчета в том, что делаем. Мы выбираем из всех воображаемых миров тот, который в каком-то внутреннем, интеллектуальном смысле ближе всего к реальности. Мы сравниваем реальность с тем, что воспринимаем как почти реальное. Благодаря этому мы получаем некое неуловимое чувство перспективы по отношению к действительности. Наш Ленивец — это странный вариант действительности: мыслящее существо, неспособное к созданию гипотетических миров (по крайней мере, он утверждает, что такой способности у него нет — но вы, вероятно, заметили, что на самом деле его речь полна контрафактов!) Подумайте, насколько беднее была бы наша интеллектуальная жизнь, если бы мы не обладали творческой способностью выбираться из реального мира в эти соблазнительные «а что, если бы…». С точки зрения изучения человеческого мышления эти экскурсы очень интересны, поскольку в большинстве случаев они происходят бессознательно. Это означает, что знание о том, что попадает в область гипотетических миров, а что нет, открывает для нас окно в подсознание.

Один из способов увидеть природу нашей мысленной метрики в перспективе состоит в том, чтобы «вышибить клин клином». Это сделано в Диалоге, где нашей «гипотетической способности» пришлось вообразить такой мир, в котором само понятие гипотетической способности действует в воображаемом мире. Первый гипотетический повтор Диалога, в котором мяч не оказывается вне игры, вообразить совсем нетрудно. На самом деле, он пришел мне в голову благодаря вполне обычному замечанию человека, сидевшего рядом со мной на футбольном матче. Это замечание меня удивило и заставило задуматься о том, почему кажется естественным вообразить именно такой гипотетический мир, а не тот, в котором изменен счет или количество штрафных. Затем я стал перебирать другие, еще менее вероятные изменения, такие, как погода (это есть в Диалоге), вид игры (тоже в Диалоге) и другие, еще более сумасбродные варианты (и это в Диалоге). Однако я заметил, что то, что смешно варьировать в одной ситуации, может оказаться легко вообразимым в другой. Например, иногда вы можете вполне естественно задуматься о том, как пошла бы игра, если мяч был другой формы (например, когда вам приходится играть в баскетбол слабо накачанным мячом); однако когда вы смотрите баскетбол по телевизору, такое просто не приходит вам в голову.

Уровни стабильности

Тогда мне показалось (и кажется до сих пор), что возможность изменения какой-либо черты события (или обстоятельства) зависит от множества вложенных один в другой контекстов, в которых это событие (или обстоятельство) нами воспринимается. Сюда хорошо подходят математические термины постоянная, параметр и переменная. Часто математики, физики и другие ученые, производя вычисления, говорят:«с — постоянная, p — параметр и v — переменная.» Они имеют в виду, что каждая из этих величин, включая постоянную, может варьироваться, но при этом существует некая иерархия изменяемости. В ситуации, представляемой символами, с устанавливает некое основное условие; p — менее основное условие, которое может варьироваться, пока с остается неизменным; и, наконец, v может меняться сколько угодно при неизменных с и p. Нет смысла представлять, что v остается фиксированным, а изменяются с и p, поскольку с и p устанавливают тот контекст, в котором v приобретает значение. Представьте себе, к примеру, зубного врача, у которого есть список его пациентов и для каждого пациента — описание его зубов. Вполне разумно (и весьма выгодно) иметь постоянного пациента и менять состояние его зубов. С другой стороны, совершенно бессмысленно пытаться оставлять неизменным какой-то определенный зуб и менять пациентов. (Разумеется, иногда наилучшим решением бывает сменить зубного врача…)

Мы строим наше мысленное представление о ситуации постепенно, слой за слоем. Низший уровень устанавливает самый глубокий аспект контекста, иногда настолько глубокий, что он вообще не может варьироваться. Например, трехмерность мира настолько вошла в наше сознание, что большинству из нас не приходит в голову воображать какие-либо вариации на эту тему. Это, так сказать, постоянная постоянная. Затем идут слои, временно устанавливающие некие зафиксированные аспекты ситуаций; их можно назвать глубинными допущениями. Это те вещи, которые мы обычно считаем за неизменные, хотя и знаем, что в принципе они могли бы измениться. Этот слой все еще можно назвать «постоянным». Например, когда мы смотрим футбол, такими постоянными являются правила игры. Далее следуют «параметры» — они могут варьироваться с большей легкостью, но мы временно принимаем их за неизменные. В нашем футбольном примере параметрами могут являться погода, команда противников и так далее. Скорее всего, существуют несколько слоев параметров. Наконец, мы достигаем самого неустойчивого аспекта ситуации — переменных. Это такие вещи, как положение «вне игры», неудачный удар по воротам и тому подобное; здесь нам легко на мгновение представить себе альтернативное положение дел.

Фреймы и вложенные контексты

Термин фрейм (кадр, группа данных) сейчас в моде среди специалистов по искусственному интеллекту; его можно определить, как численное представление данного контекста. Этот термин, как и многие идеи о фреймах, обязан своим происхождением Марвину Минскому, хотя само это понятие витало в воздухе уже несколько лет. Можно сказать, что мысленные представления о ситуациях включают фреймы, вложенные один в другой. Каждый из аспектов ситуации обладает собственным фреймом. Такие вложенные фреймы напоминают мне множество комодов. Выбирая фрейм, вы выбираете определенный комод. В него может быть вставлено несколько ящиков — «подфреймов». При этом каждый из этих ящиков, в свою очередь, является комодом. Как можно вставить целый комод в отверстие для одного-единственного ящика? Проще простого — надо уменьшить и деформировать второй комод. В конце концов, он ведь не физический предмет, а воображаемый! Во внешнем комоде может быть несколько разных гнезд, куда должны быть вставлены ящики; затем мы начинаем вставлять ящики в гнезда внутренних комодов (или подфреймов). Этот процесс может продолжаться рекурсивно.

Живая сюрреалистическая картина того, как комод сплющивают и сгибают, чтобы запихать его в гнездо любой величины, очень важна, так как она намекает на то, что наши понятия сплющиваются и сгибаются в зависимости от контекстов, в которые мы их запихиваем. Что происходит с вашим представлением о «человеке», когда вы думаете о футболистах? Безусловно, это искаженное представление, навязанное вам общим контекстом. Вы засунули фрейм «человек» в гнездо фрейма «футбольный матч». Теория представления знаний в форме фреймов опирается на идею, что мир состоит из почти закрытых подсистем, каждая из которых может служить контекстом для других, при этом они не слишком прерываются и почти не причиняют перебоев в процессе.

Одна из основных идей, касающихся фреймов, состоит в том, что каждый фрейм ожидает некоего определенного содержания. Этому образу соответствуют комоды, в каждом гнезде которых есть по встроенному, но непрочно закрепленному ящику под названием значение по умолчанию. Если я попрошу вас представить себе берег реки, у вас в голове появится некая картина; однако большинство ее черт могут быть изменены, если я добавлю какие-либо детали: «во время засухи», или «в Бразилии», или «без пляжа». Благодаря значениям по умолчанию рекурсивный процесс заполнения гнезд может быть завершен. В самом деле, вы можете сказать: «Я заполню гнезда на трех уровнях, а дальше буду пользоваться значениями по умолчанию.» Взятый вместе с этими значениями фрейм содержит информацию о собственных границах и эвристику для переключения на другие фреймы в том случае, если эти границы нарушаются.

Многоуровневая структура фрейма дает возможность увидеть его крупным планом и рассмотреть все его детали с какого угодно приближения. Для этого надо только сосредоточить внимание на соответствующем фрейме, затем на одном из его подфреймов и так далее, пока вы не получите всех требуемых деталей. Это похоже на дорожный атлас России, в котором кроме карты страны на первой странице есть карты областей, областных центров и даже некоторых небольших городов, если вам понадобится больше сведений. Можно вообразить себе атлас с каким угодно количеством деталей, включая кварталы, дома, комнаты и так далее — словно вы смотрите в телескоп с линзами разной мощи, каждая из которых имеет свое предназначение. Важно то, что можно свободно выбирать между различными масштабами; детали часто бывают неважны и только мешают.

Поскольку сколь угодно разные фреймы можно засунуть в гнезда других фреймов, возможны конфликты и «столкновения». Схема аккуратно организованного всеобщего множества слоев «постоянных», «параметров» и «переменных» — всего лишь упрощение. На самом деле, у каждого фрейма есть собственная иерархия изменяемости. Именно поэтому анализ нашего восприятия такой сложной игры как футбол, со множеством подфреймов, подподфреймов и так далее, представляется весьма запутанной операцией. Каким образом все эти фреймы взаимодействуют между собой? Как разрешаются конфликты, когда один фрейм утверждает: «Это постоянная», а другой в то же время говорит: «Это переменная»? Я не могу дать ответа на эти глубокие и сложные вопросы теории фреймов. Пока еще не достигнуто соглашение по поводу того, что в действительности представляют из себя фреймы и как можно использовать их в программах ИИ. Некоторые из моих предположений на этот счет вы найдете в следующем разделе, в котором говорится о некоторых задачах в области узнавания зрительных структур — я называю их «задачами Бонгарда».

Задачи Бонгарда

Задачи Бонгарда (ЗБ) — это проблемы, подобные тем, которые предложил в своей книге «Проблема узнавания» русский ученый Михаил Моисеевич Бонгард. На рис. 119 показана типичная ЗБ — #51 из ста задач, приведенных в книге.

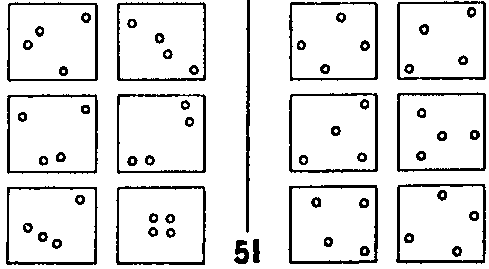
Рис. 119. Задача Бонгарда #51. (Из книги М. Бонгарда «Проблема узнавания».)

Эти интереснейшие задачи могут быть предложены людям, компьютерам или даже представителям внеземных цивилизаций. Каждая задача состоит из двенадцати фигур, взятых в рамку (они так и называются рамками): шесть левых рамок составляют класс I, шесть правых — класс II. Рамки можно пронумеровать следующим образом:

I-А I-Б  II-А II-Б

I-В I-Г  II-В II-Г

I-Д I-Е  II-Д II-Е

Задача состоит в том, чтобы обнаружить, чем рамки класса I отличаются от рамок класса II.

В программе для решения задач Бонгарда было бы несколько ступеней, на которых первичные данные постепенно превращались бы в описания. Ранние ступени относительно негибки; гибкость последующих ступеней увеличивается. Последние ступени обладают свойством, которое я называю «экспериментальностью». Это означает, что на этой стадии представление о картине всегда пробное. Описание высшего уровня может быть переделано в любой момент при помощи приемов, используемых на последних ступенях. Идеи, представленные ниже, также экспериментальны. Сначала я попытаюсь дать общие идеи, не останавливаясь на трудностях; затем постараюсь объяснить все тонкости, трюки и так далее. Таким образом, ваше понимание того, как это все работает, может изменяться по мере того, как вы читаете дальше. Это будет как раз в духе нашей дискуссии!

Предварительная обработка выбирает мини-словарь

Представьте себе, что дана некая задача Бонгарда. Прежде всего, телекамера считывает первичные данные. Затем эти данные проходят предварительную обработку. Это значит, что в них выделяются наиболее важные черты. Названия этих черт составляют «мини-словарь» задачи; они выбираются из общего «словаря выдающихся черт». Вот некоторые типичные термины из этого словаря:

отрезок, поворот, горизонтальный, вертикальный, черный, белый, маленький, большой, остроконечный, круглый…

На второй стадии предварительной обработки используются некоторые знания об элементарных фигурах; если таковые обнаруживаются, их названия также включаются в мини-словарь. Здесь могут быть выбраны такие термины:

треугольник, круг, квадрат, углубление, выступ, прямой угол, вершина, точка пересечения, стрелка…

Приблизительно в этот момент в человеческом интеллекте встречаются сознательное и бессознательное. Что же происходит потом?

Описания высшего уровня

После того, как ситуация до некоторой степени «понята» в знакомых нам терминах, программа «оглядывается кругом» и предлагает пробное описание одной или нескольких рамок. Эти описания весьма просты. Например:

наверху, внизу, справа от, слева от, внутри, снаружи, близко от, далеко от, параллельно, перендикулярно, в ряд, рассеяны, на равном расстоянии друг от друга, на неравном расстоянии друг от друга и т. д.

Могут использоваться также определенные и неопределенные числовые описания:

1,2,3,4,5, … много, несколько и т. д

Могут быть построены и более сложные описания, такие как:

правее, менее близко к, почти параллельно и т. д.

Таким образом, типичная рамка — скажем, 1-Е из ЗБ #47 (рис. 120) — может быть описана различными способами. Можно сказать, что в ней имеются:

три фигуры

или

три белых фигуры

или

один круг направо

или

два треугольника и круг

или

два повернутых кверху треугольника

или

одна большая фигура и две маленьких фигуры

или

одна изогнутая фигура и две прямолинейных фигуры

или

круг с одной и той же фигурой внутри и снаружи него.

Рис. 120. Задача Бонгарда # 47. (Из книги Бонгарда «Проблема узнавания»)

Каждое из этих описаний рассматривает рамку сквозь некий «фильтр». Вне контекста, каждое из описаний может быть полезно. Однако оказывается, что в контексте данной задачи все они «ошибочны». Иными словами, зная различие между классами I и II, вы не смогли бы, исходя только из этих описаний, сказать, к какому классу принадлежит данная рамка. В данном контексте основной чертой описываемой рамки является то, что она включает:

 круг с треугольником внутри.

Обратите внимание, что человек, услышавший это описание, не сможет восстановить оригинальную картинку, однако сумеет узнать картинки, отличающиеся данной чертой.

Это напоминает музыкальный стиль: вы можете безошибочно распознавать произведения, написанные Моцартом, и в то же время быть неспособным написать ничего похожего на его музыку.

Взгляните теперь на рамку I-Г задачи #91 (Рис. 121). Перегруженным, но «верным» описанием в контексте ЗБ #91 будет:

круг с тремя прямоугольными выемками.

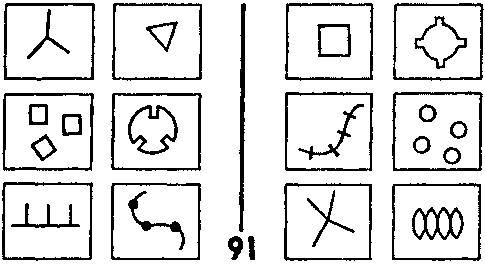
Рис. 121. Задача Бонгарда # 91. (Из книги Бонгарда «Проблема узнавания».)

Обратите внимание, насколько сложно это описание: слово «с» действует в нем как отрицание, давая понять, что «круг», на самом деле, не является кругом — это почти круг, но… Более того, выемки не являются полными прямоугольниками. В нашем использовании языка для описания предметов есть немало тонкостей. Ясно, что большое количество информации здесь опущено и можно было бы опустить еще больше. A priori очень трудно понять, какую информацию лучше отбросить, а какую необходимо сохранить. Поэтому нам нужно, путем эвристики, закодировать некий метод для разумного компромисса. Разумеется, если нам необходимо восстановить отброшенную информацию, мы всегда можем спуститься на низшие уровни описания (к менее блочной картине), так же как люди могут все время обращаться к данной задаче Бонгарда с тем, чтобы проверить правильность их догадок. Таким образом, метод состоит в создании правил, объясняющих, как

создавать пробные описания для каждой рамки;

сравнивать их с пробными описаниями других рамок каждого класса

переделывать описания

(1) добавляя информацию;

(2) отбрасывая информацию;

(3) рассматривая ту же информацию под другим углом.

Этот процесс повторяется до тех пор, пока мы не найдем различия между двумя классами.

Эталоны и детектор сходства

Хорошей стратегией было бы построение описаний, как можно более структурно схожих между собой, поскольку любая схожая структура облегчает процесс сравнения. К этой стратегии относятся два важных элемента теории. Один из них — идея «описания-схемы» или эталона; другой — идея детектора сходства.

Сначала рассмотрим детектор сходства. Это особый активный элемент, присутствующий на всех уровнях программы (На разных уровнях могут быть детекторы различных типов.) Он беспрерывно работает, проверяя индивидуальные описания и сравнивая их между собой в поисках черт, повторяющихся от одного описания к другому. Обнаружение сходства приводит в действие операции, изменяющие одно или несколько описаний.

Теперь перейдем к эталонам. После окончания обработки данных мы сразу пытаемся создать эталон или схему описаний — один и тот же формат для описаний всех рамок данной задачи. Идея здесь состоит в том, что каждое описание может быть разбито на несколько подописаний, а те, если это необходимо, в свою очередь могут быть разбиты на подподописания. Вы достигаете дна, спускаясь к примитивным понятиям на уровне препроцессора. Важно найти такой способ разбивания на подпрограммы, который отразил бы общность между всеми рамками; иначе «псевдо-порядок», который вы введете в мир, окажется бессмысленным и ненужным.

На основе какой информации строятся эталоны? Рассмотрим это на примере. Возьмем ЗБ #49 (рис. 122). Предварительная обработка информации сообщает нам, что каждая рамка состоит их нескольких маленьких «о» и большой замкнутой кривой. Эти ценные сведения стоит включить в эталон. Таким образом, наша первая попытка создания эталона выглядит так:

большая замкнутая кривая: —

маленькие «о»: —

Это очень просто: в описании-эталоне есть два гнезда, куда надо будет вставить подописания.

Рис. 122. Задача Бонгарда #49. (Из книги Бонгарда «Проблема узнавания»).

Гетерархическая программа

Теперь происходит интересная вещь, вызванная к жизни словами «замкнутая кривая». Один из важнейших узлов в программе — это нечто вроде семантической сети или сети понятий, в которой все известные программе существительные, прилагательные и так далее связаны и соотнесены между собой. Например, «замкнутая кривая» тесно связана с понятиями «внутри» и «снаружи». Сеть понятий битком набита информацией о связях между терминами: она говорит нам, что противоположно чему, что сходно с чем, какие вещи часто встречаются вместе и так далее. Небольшой кусочек концептуальной сети показан на рис. 123; я объясню его позже. Пока давайте вернемся к задаче #49. Понятия «внутри» и «снаружи» активируются благодаря тому, что в сети понятий они находятся вблизи от «замкнутой кривой». Это влияет на постройку эталона, в который вводятся гнезда для внутренней и внешней сторон кривой. Таким образом, вторым приближением эталона является:

большая замкнутая кривая: —

маленькие «о» внутри: —

маленькие «о» снаружи: —

В поисках дальнейших подразделений, термины «внутри» и «снаружи» заставят процедуры программы рассмотреть эти районы рамки. В районе рамки I-A ЗБ #49 обнаруживается следующее:

большая замкнутая кривая: круг

маленькие «о» внутри: три

маленькие «о» снаружи: три

Описанием рамки II-А той же задачи может быть:

большая замкнутая кривая: сигара

маленькие «о» внутри: три

маленькие «о» снаружи: три

В этот момент детектор сходства, работающий параллельно с другими операциями, обнаруживает повторение понятия «три» во всех гнездах, описывающих «о»; этого оказывается достаточно, чтобы снова модифицировать эталон. Обратите внимание, что первая модификация была предложена сетью понятий, а вторая — детектором сходства. Теперь наш эталон для задачи #49 приобретает такой вид:

большая замкнутая кривая: —

три маленьких «о» внутри: —

три маленьких «о» снаружи: —

Теперь, когда «три» поднялось уровнем выше и вошло в эталон, имеет смысл обратиться к его соседям по сети понятий. Один их них — «треугольник», что означает, что треугольники, состоящие из «о», могут оказаться важными для решения задачи. В результате оказывается, что эта дорога заводит в тупик, — но как мы могли знать об этом заранее? Человек, решающий эту задачу, скорее всего пошел бы тем же путем, так что хорошо, что наша программа нашла эту дорогу.

Описание рамки II-Д может быть таким:

большая замкнутая кривая: круг

три маленьких «о» внутри: равносторонний треугольник

три маленьких «о» снаружи: равносторонний треугольник

Разумеется, при этом было отброшено огромное количество информации о размерах, положении и ориентации этих треугольников и т. п. Но именно в этом и заключается смысл создания описаний вместо использования необработанных данных! Это похоже на «воронку», которую мы обсуждали в главе XI.

Сеть понятий

Нам не понадобится рассматривать решение задачи #49 целиком, поскольку мы уже показали, каким образом индивидуальные описания, эталоны, детектор сходства и сеть понятий непрерывно взаимодействуют между собой. Рассмотрим более подробно, что представляет из себя сеть понятий и каковы ее функции. Упрощенный ее фрагмент, приведенный на рис. 123, кодирует следующие идеи:

«высоко» и «низко» противоположны.

«сверху» и «снизу» противоположны.

«высоко» и «сверху» схожи.

«низко» и «снизу» схожи.

«справа» и «слева» противоположны.

различие между «справа-слева» подобно различию между «высоко-низко».

«противоположно» и «схоже» противоположны.

Обратите внимание, что мы можем говорить как об узлах, так и о связях сети. В этом смысле ни один объект в сети не находится уровнем выше другого. В другой части данной схемы закодированы следующие понятия:

Квадрат — это многоугольник.

Треугольник — это многоугольник.

Многоугольник — это замкнутая кривая.

Разница между треугольником и квадратом в том, что у первого 3 стороны, а у второго — 4.

4 схоже с 3.

Круг — это замкнутая кривая.

У замкнутой кривой есть внутренний и внешний районы. «Внутри» и «снаружи» противоположны.

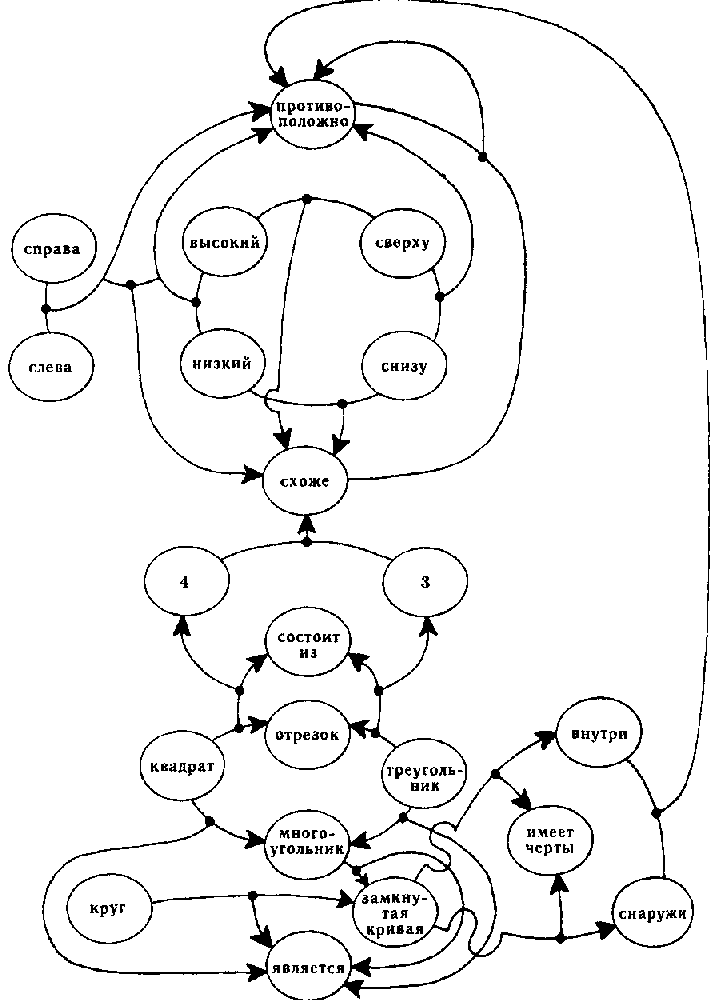
Рис. 123. Небольшая часть сети понятий программы для решения задач Бонгарда. «Узлы» соединены между собой «связями», которые, в свою очередь, могут быть связаны. Принимая связи за глаголы, а соединенные ими узлы за подлежащие и дополнения, можно построить на основе этой диаграммы разные русские предложения.

Сеть понятий очень широка. Кажется, что знания закодированы в ней только статистически, или декларативно, — но это верно лишь наполовину. На самом деле, ее знания граничат с процедурными, потому что сходство в сети действует как гид, или «подпрограммы», сообщая основной программе, как лучше понимать картинки в рамках.

Например, какая-нибудь из первых догадок может оказаться ошибочной, но при этом содержать зерно правильного ответа При первом взгляде на ЗБ #33 (рис. 124) можно подумать, что класс I содержит «колючие» фигуры, а класс II — «гладкие». Однако, если присмотреться, эта догадка оказывается неверной. Все же в ней есть ценная информация, и можно попытаться развить эту идею дальше, работая с теми понятиями сети, которые связаны с «колючим». Это понятие схоже с «острым», которое и оказывается отличительной чертой класса I. Таким образом, одна из основных функций сети понятий состоит в том, чтобы позволять модификацию ранних ошибочных идей и переход к вариациям, которые могут оказаться правильными.

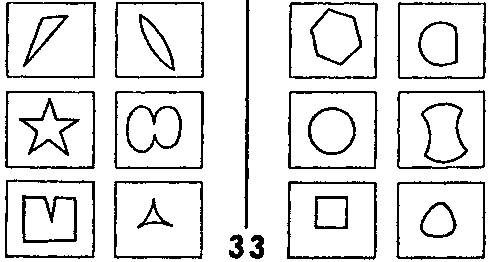
Рис. 124 Задачи Бонгарда.

Переход и пробность

Понятие перехода между похожими предметами родственно понятию восприятия одного предмета как вариации другого. Мы уже видели прекрасный пример этого — «круг с тремя выемками», который на самом деле вовсе не круг! Наши понятия должны быть до определенной степени гибкими. Ничто не должно оставаться совершенно неизменным. С другой стороны, они также не должны быть настолько бесформенными, что в них пропадет всякое значение. Все дело в том, чтобы знать, когда одно понятие может перейти в другое.

Такой переход лежит в основе решений задач Бонгарда ##85 — 87 (рис. 125). ЗБ #85 довольно проста. Предположим, что наша программа в процессе  предварительной обработки данных узнает некий «отрезок». После этого ей легко посчитать отрезки и найти различие между классом I и классом II в ЗБ #85.

Теперь программа переходит к задаче #86. Ее основная методика состоит в том, чтобы опробовать все недавние идеи, оказавшиеся удачными. В реальном мире повторение сработавших ранее приемов часто увенчивается успехом, и Бонгард в своих задачах не стремится перехитрить этот тип эвристики—к счастью, он даже поощряет его. Таким образом, мы переходим к ЗБ #86, имея на вооружении две идеи («считать» и «отрезок»), слитые в одну: «считать отрезки». Но оказывается, что в ЗБ #86 вместо отрезков нужно считать последовательности линий. Последовательность линий здесь означает сцепление (одного или более) отрезков. Программа может догадаться об этом, например, благодаря тому, что ей известны оба понятия, «отрезок прямой» и «последовательность прямых», и что они расположены близко друг от друга в сети понятий. Другим, способом было бы изобретение понятия «последовательность прямых» — задача, мягко выражаясь, не из простых.

Далее следует ЗБ #87, в которой понятие «отрезок» обыгрывается по-иному. Когда один отрезок становится тремя? (См. рамку II-А.) Программа должна быть достаточно гибкой, чтобы переходить взад и вперед между различными описаниями данного фрагмента рисунка. Разумно сохранять в памяти старые описания, вместо того, чтобы их забывать и затем составлять снова, поскольку нет гарантии того, что новое описание окажется лучше прежнего. Таким образом, вместе с каждым старым описанием программа должна запоминать его сильные и слабые стороны. (Не правда ли, это начинает звучать довольно сложно?)

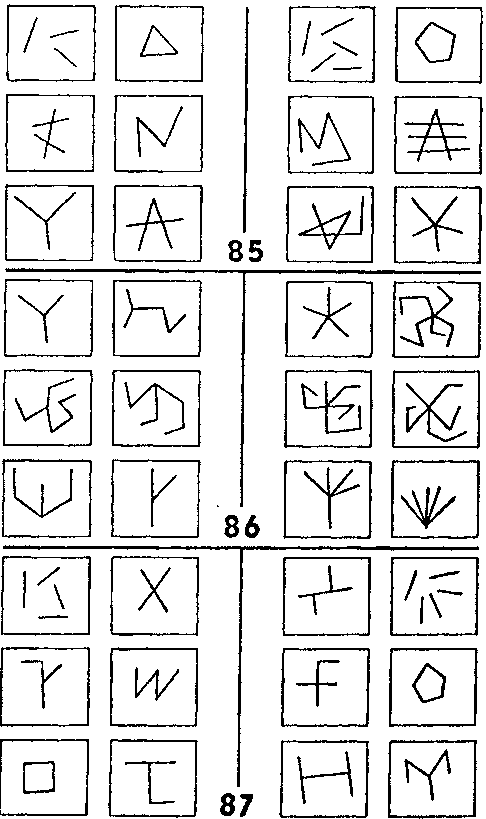
Рис. 125. Задачи Бонгарда ##85 — 87 (Из книги Бонгарда «Проблема узнавания»).

Мета-описания

Теперь мы подошли к другой жизненно важной части процесса узнавания; она имеет дело с уровнями абстракции и мета-описаниями. Для примера давайте вернемся к ЗБ #91 (рис. 121). Какой эталон можно здесь построить? С таким количеством вариантов трудно знать, откуда начинать. Но это уже само по себе является подсказкой! Это говорит нам, что различие между классами, скорее всего, существует на уровне, высшем чем уровень геометрических описаний. Это наблюдение подсказывает программе, что она может попытаться рассмотреть описания описаний — то есть мета-описания. Может быть, на этом втором уровне нам удастся обнаружить какие-либо общие черты, и, если повезет, найти достаточно сходства для того, чтобы создать эталон для мета-описаний. Таким образом, мы начинаем работу без эталона и создаем описания нескольких рамок; после того, как они закончены, мы описываем сами эти описания. Какие гнезда будут у нашего эталона для мета-описаний? Может быть, следующие:

использованные понятия: —

повторяющиеся понятия: —

названия гнезд: —

использованные фильтры: —

Существует множество других гнезд, которые могут быть использованы в мета-описаниях; это просто пример. Предположим теперь, что мы описали рамку I-Д в ЗБ #91. Ее «безэталонное» описание может выглядеть так:

горизонтальный отрезок.

вертикальный отрезок, находящийся на горизонтальном отрезке.

вертикальный отрезок, находящийся на горизонтальном отрезке.

вертикальный отрезок, находящийся на горизонтальном отрезке.

Разумеется, множество сведений было отброшено: то, что три вертикальных отрезка одинаковой длины, отстоят друг от друга на одно и то же расстояние и т. п. Но возможно и подобное описание. Мета-описание может выглядеть так:

использованные понятия: вертикальный-горизонтальный, отрезок, находящийся на

повторяющиеся понятия: 3 копии описания «вертикальный отрезок, находящийся на горизонтальном отрезке».

названия гнезд: —

использованные фильтры: —

Не все гнезда мета-описания должны быть заполнены: на этом уровне тоже возможно отбрасывание информации, как и на уровне «простого описания». Если бы мы теперь захотели составить описание и мета-описание любой другой рамки класса I, то гнездо «повторяющиеся описания» каждый раз содержало бы фразу «три копии ...» Детектор сходства заметил бы это и выбрал бы «тройничность» в качестве общей абстрактной черты рамок класса I. Таким же образом, путем мета-описаний может быть установлено, что «четверичность» — отличительная черта класса II.

Важность гибкости

Вы можете возразить, что использование мета-описаний в данном случае напоминает стрельбу по мухам из пушки, поскольку тройничность и четверичность могли быть найдены уже на первом уровне, если бы мы построили наше описание немного иначе. Это верно, но для нас важно иметь возможность решать эти задачи различными путями. Программа должна быть очень гибкой; она не должна быть обречена на провал, если ее «занесет» не туда. Я хотел проиллюстрировать общий принцип: когда построение эталона затруднено, потому что препроцессор запутывается среди различных деталей, это показывает, что здесь задействованы понятия на высших уровнях, о которых препроцессор ничего не знает.

Фокусирование и фильтрование

Теперь давайте рассмотрим другой вопрос: каким образом можно отбрасывать информацию. Ответ на этот вопрос включает два родственных понятия, которые я называю «фокусированием» и «фильтрованием». Фокусирование означает составление описания так, что оно сосредотачивается на каком-то одном районе картинки и «сознательно» оставляет без внимания все остальные. Фильтрование означает составление описания так, что оно видит содержимое картинки под каким-то определенным углом, и сознательно игнорирует все другие аспекты.

Таким образом, они дополняют друг друга: фокусирование имеет дело с объектами (грубо говоря, с существительными), а фильтрование — с понятиями (грубо говоря, с прилагательными).

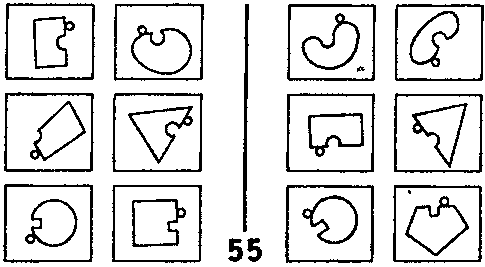
Рис. 126. Задача Бонгарда #55 (Из книги Бонгарда «Проблема узнавания»).

Для примера фокусирования рассмотрим ЗБ #55 (рис. 126). Здесь мы сосредотачиваемся на выемке и маленьком круге около нее, и оставляем без внимания все остальное. ЗБ #22 — это пример фильтрования. Мы отбрасываем все понятия, кроме размера. Для решения ЗБ #58 (рис. 128) требуется комбинация фокусирования и фильтрования.

Одним из важных способов получения идей для фокусирования и фильтрования является другой тип «фокусирования»: детальный анализ какой-либо особенно простой рамки — скажем, рамки с наименьшим количеством предметов. Очень полезным может оказаться сравнение между гобой простейших рамок обоих классов.

Но каким образом программа определяет, какие рамки самые простые, до того, как она производит их описание? Одним из способов определения простоты является поиск рамки с наименьшим количеством черт, найденных препроцессором. Это может быть сделано на ранних стадиях работы, поскольку для этого не нужен готовый эталон; на самом деле, это может быть использовано как поиск черт для включения в эталон. ЗБ #61 (рис. 129) — пример случая, когда такая техника дает плоды очень быстро.

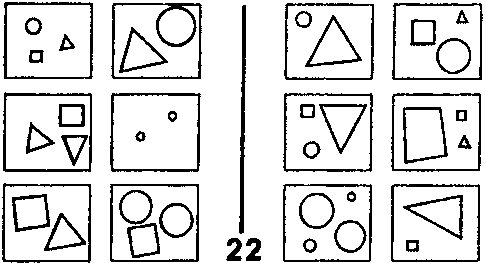
Рис. 127. Задача Бонгарда #22 (Из книги Бонгарда «Проблема узнавания»).

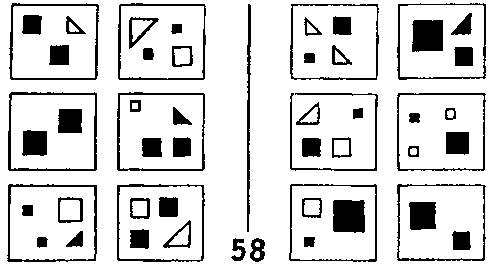
Рис. 128. Задача Бонгарда #58. (Из книги Бонгарда «Проблема узнавания»).

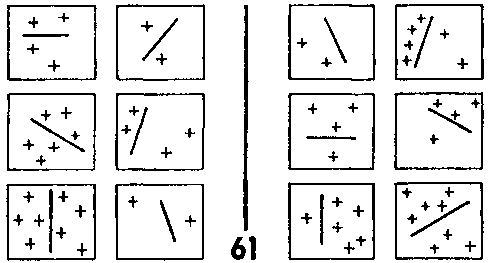
Рис. 129. Задача Бонгарда #61. (Из книги Бонгарда «Проблема узнавания»).

Наука и мир задач Бонгарда

Задачи Бонгарда можно интерпретировать как крохотную модель мира, занимающегося «наукой» — то есть поисками упорядоченных структур. В процессе этих поисков создаются и переделываются эталоны, гнезда переносятся с одного уровня обобщения на другой, используются фокусирование и фильтрование и т. д.

На каждом уровне сложности делаются свои открытия. Теория американского философа Куна о том, что странные события, которые он называет сдвигами парадигмы, отмечают границу между «нормальной» наукой и «концептуальными революциями», не кажется подходящей к нашему случаю, поскольку в данной системе сдвиги парадигмы происходят все время и на всех уровнях. Это объясняется гибкостью описаний.

Разумеется, некоторые открытия более «революционны», чем другие, поскольку они производят больший эффект. Например, мы можем обнаружить, что задачи #70 и #72 представляют из себя «одну и ту же задачу», рассмотренную на достаточно абстрактном уровне. Основная идея здесь в том, что в обеих задачах используется понятие «вложения» на глубине 1 и 2. Это новый уровень открытия в задачах Бонгарда. Существует еще более высокий уровень, касающийся всех картинок как целого. Если кто-либо не видел этого собрания, интересной задачей для него было бы попытаться представить себе, как эти картинки выглядят. Это было бы революционным открытием, хотя механизмы, которые при этом оперируют, не отличаются от механизмов, помогающих нам решать отдельные задачи Бонгарда.

По той же причине, настоящая наука не делится на «нормальные» периоды и периоды «концептуальных революций», сдвиги парадигм происходят в ней постоянно, большие и маленькие, на различных уровнях. Рекурсивные графики INT и график G (рис. 32 и 34) дают нам геометрическую модель этой идеи. Их структура полна скачков на всех уровнях, причем чем ниже уровень, тем меньше скачки.

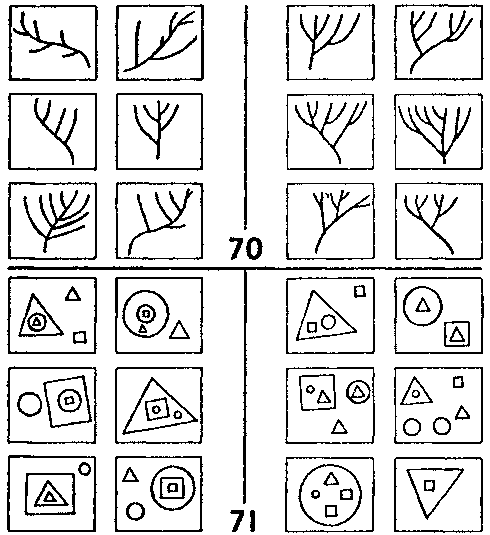
Рис. 130. Задачи Бонгарда ##70-71 (Из книги Бонгарда «Проблема узнавания»).

Связи с другими типами мысли

Чтобы поместить эту программу в контекст, я хочу упомянуть о том, как она соотносится с другими аспектами познания. Она зависит от других аспектов познания, а те, в свою очередь, зависят от нее. Поясню сначала ее зависимость от других аспектов познания. Интуиция, подсказывающая нам когда имеет  смысл стереть различия, попытаться составить иное описание, вернуться по собственным следам, перейти на другой уровень и так далее, приходит только с общим опытом мышления. Поэтому так трудно определить эвристику для этих основных аспектов программы. Иногда наш опыт реального мира сложным образом влияет на то, как мы описываем и переописываем рамки. Например, кто может сказать, насколько знакомство с настоящими деревьями помогает в решении задачи #70? Маловероятно, что человеческая сеть понятий, относящихся к решению этих задач, может быть легко отделена от остальной сети понятий. Скорее интуиция, которую мы получили от созерцания и контакта с реальными предметами — расчески, поезда, цепочки, кубики, буквы, резинки и т. д., и т. п. — играет незаметную, но важную роль в решении подобных задач.

И наоборот, понимание ситуаций реального мира наверняка в большой степени зависит от зрительных образов и пространственной ориентации — таким образом, гибкий и эффективный способ представлять различные структуры (такие, как задачи Бонгарда) может только способствовать общей эффективности мыслительных процессов.

Мне кажется, что задачи Бонгарда были разработаны очень тщательно: в них есть некая универсальность, в том смысле, что у каждой из них — единственный правильный ответ. Разумеется, с этим можно спорить, утверждая, что то, что мы считаем «правильным», зависит от того, что мы — люди. Инопланетянин может совершенно с нами не согласиться. Несмотря на то, что у меня нет никакого конкретного свидетельства в пользу той или иной теории, я все-таки считаю, что задачи Бонгарда зависят от некоего чувства простоты и что люди — не единственные существа, обладающие этим чувством. То, что для этого важно быть знакомым с типично земными предметами, такими как расчески, поезда, резинки и тому подобное, не противоречит утверждению о том, что некое чувство простоты универсально, поскольку здесь важны не отдельные предметы, а тот факт, что вкупе они покрывают некое широкое пространство. Скорее всего, другие цивилизации будут обладать таким же большим репертуаром предметов и натуральных объектов и таким же обширным опытом. Поэтому мне кажется, что умение решать задачи Бонгарда находится близко к тому, что можно назвать «чистым» разумом — если таковой существует. Следовательно, с них можно начинать, если мы хотим изучить умение находить некое присущее схемам или сообщениям значение. К несчастью, мы привели здесь только небольшую часть этого замечательного собрания. Надеюсь, что многие читатели познакомятся со всем собранием, приведенным в книге Бонгарда (см. Библиографию).

Некоторые проблемы узнавания структур, которые полностью вросли в наше подсознание, довольно удивительны. Они включают:

узнавание лиц (неизменность лиц при возрастных изменениях, различных выражениях, разном освещении, разном расстоянии, под другим углом зрения и так далее);

узнавание тропинок в лесах и в горах — почему-то это всегда казалось мне одним из наиболее удивительных случаев узнавания схем. Однако это умеют делать и животные…

прочтение текста, написанного сотней, если не тысячей различных шрифтов.

Языки, рамки и символы, передающие сообщения

Одним из способов решения проблемы узнавания структур и других сложных проблем ИИ является так называемый «актерский» формализм Карла Хьюитта, подобный языку «Smalltalk», разработанному Аланом Кэйем и другими. Он заключается в том, что программа пишется в виде набора взаимодействующих актеров, которые могут обмениваться сложными сообщениями. Это чем-то напоминает гетерархическое собрание процедур, вызывающих друг друга. Основное различие состоит в том, что процедуры передают друг другу небольшое количество информации, в то время как сообщения, которыми обмениваются актеры, могут быть сколь угодно длинными и сложными.

Благодаря своему умения передавать сообщения, актеры становятся в каком-то смысле автономными агентами — их можно даже сравнить с самими компьютерами, а сообщения — с программами. Каждый актер может интерпретировать данное сообщение по-своему; таким образом, значение сообщения будет зависеть от актера, его получившего. Это объясняется тем, что в актерах есть часть программы, которая интерпретирует сообщения; поэтому интерпретаторов может быть столько же, сколько и актеров. Разумеется, интерпретаторы многих актеров могут оказаться идентичными; в действительности, это может быть большим преимуществом (так же важно, чтобы в клетке было множество плавающих в цитоплазме идентичных рибосом, каждая из которых будет интерпретировать сообщение — в данном случае, мессенджер ДНА — одинаковым образом).

Интересно подумать, как можно соединить понятие фреймов с понятием актеров. Давайте назовем фрейм, способный создавать и интерпретировать сложные сообщения, символом:

фрейм + актер = символ

Мы будем говорить здесь о том, как можно представить те неуловимые активные символы, которые обсуждались в главах XI и XII; поэтому в данной главе «символ» будет иметь то же значение. Не расстраивайтесь, если вы не сразу поймете, каким образом может произойти этот синтез. Это, действительно, неясно, — но это одно из самых многообещающих направлений исследований в ИИ. Более того, несомненно, что даже наилучшие синтетические представления будут менее мощными, чем символы человеческого мозга. В этом смысле, пожалуй, еще рановато называть объединения фреймов с актерами «символами», но это — оптимистический взгляд на вещи.