ГЛАВА V: Рекурсивные структуры и процессы
ГЛАВА V: Рекурсивные структуры и процессы
Что такое рекурсия?
ЧТО ТАКОЕ РЕКУРСИЯ? То, что было проиллюстрировано в диалоге «Маленький гармонический лабиринт»: вложенность схем одна в другую и варианты этой вложенности. Рекурсия — весьма общее понятие. (Рассказы внутри рассказов, фильмы внутри фильмов, картины внутри картин, матрешечки внутри матрешек (даже скобки внутри скобок!) — вот лишь несколько симпатичных примеров.) Однако читатель должен иметь в виду, что в этой главе термин «рекурсия» употребляется в ином значении, чем в главе III, и эти два значения связаны только косвенно. Эта связь должна проясниться к концу главы.
Иногда рекурсия приближается к парадоксу. Например, существуют рекурсивные определения. С первого взгляда может показаться, что в этом случае нечто определяется через себя самоё. Из этого получился бы если не парадокс, то порочный круг и бесконечное возвращение к началу. На самом деле, правильно сформулированное рекурсивное определение никогда не приводит ни к тому, ни к другому. Дело в том, что рекурсивные определения никогда не определяют предметы или идеи через них самих — вместо этого они используют более простые версии определяемого понятия. Чтобы вам стало понятнее, что я имею в виду, приведу несколько примеров рекурсивных определений.
Один из часто встречающихся типов рекурсии в повседневной жизни — это прекращение какого-либо дела на время, с тем, чтобы сделать более простое дело, зачастую того же типа, что и первое. Вот хороший пример. У директора фирмы на столе стоит сложный телефон, по которому ему могут звонить несколько человек одновременно. Директор разговаривает с А; в этот момент звонит Б. Директор спрашивает А, может ли тот подождать минутку. На самом деле, ему совершенно все равно, может ли А подождать, — он просто нажимает кнопку и переключается на разговор с Б. Тут звонит В. Теперь уже и Б приходится подождать. Так может продолжаться до бесконечности — однако не будем увлекаться. Предположим, разговор с В закончился; наш директор «выталкивается» обратно и продолжает беседу с Б. Между тем, на другом конце провода А в раздражении барабанит пальцами по столу и слушает сладенькие мелодии, передающиеся по телефону чтобы скрасить его ожидание… Самый простой случай был бы, если бы звонок Б закончился и директор наконец вернулся бы к А. Но может случиться, что когда он разговаривает с Б, звонит Д. Б снова оказывается «протолкнутым» в стек ждущих своей очереди. По окончанию разговора с Д директор вернется к Б, а затем к А. Разумеется, здесь он действует совершенно механически — я пытаюсь показать рекурсию в самой чистой форме.
Проталкивание, выталкивание и стек
В предыдущем примере я ввел основные термины, касающиеся рекурсии, по крайней мере так, как их понимают специалисты по компьютерам: проталкивание, выталкивание и стек. Все эти термины связаны между собой. Они вошли в обиход в конце 1950-х годов в составе ИПЛ, одного из первых языков для искусственного разума. Вы уже встречались с «проталкиванием» и «выталкиванием» в Диалоге; однако я объясню здесь эти термины еще раз. Протолкнуть означает прервать работу над очередным делом, при этом не забывая, на чем вы остановились, и начать работать над следующим заданием. Обычно говорят, что новое дело находится на «низшем уровне» по сравнению с предыдущим занятием. Вытолкнуть означает обратное: прекратить работу на одном уровне и вновь приняться за работу на высшем уровне, начав с того, на чем вы остановились.
Как же нам удается точно помнить, где мы были на каждом уровне? Для этого мы сохраняем нужную информацию в стеке. Таким образом, стек — это просто табличка, сообщающая нам 1) на чем было прервано каждое незаконченное занятие (на компьютерном жаргоне это называется «обратный адрес») и 2) какие факты нам надо знать о моменте, когда задание было прервано («переменная связка»). Когда вы выталкиваетесь наверх, чтобы возобновить работу над чем-либо, именно стек восстанавливает ваш контекст, чтобы вы не потерялись. В примере с телефонными звонками стек сообщает вам, кто ждет вас на каждой линии и в каком месте беседа была прервана.
К слову сказать, происхождение терминов «проталкивать», «выталкивать» и «стек» восходит к образу сложенных один на другой подносов в кафетерии (stack по-английски — куча, стеллаж). Обычно внизу такой стопки помещается нечто вроде пружины, поддерживающей верхний поднос приблизительно на одном и том же уровне — так что каждый новый поднос «проталкивает» всю стопку вниз, в то время как при снятии одного подноса все стопка «выталкивается» наверх.
Еще один пример из повседневной жизни. Когда вы слушаете новости по радио, часто случается, что слово предоставляется иностранному корреспонденту. «Говорит Адам Зайчиков из Минска, Беларусь.» Адам, в свою очередь, включает запись местного репортера, берущего у кого-то интервью: «С вами Иван Петровский; я нахожусь недалеко от того места, где совершилось ограбление банка. Предоставляю слово главе оперативной группы…» Теперь вы уже тремя уровнями ниже. Может случиться, что и тот, у кого берут интервью, тоже включит какую-то запись. Спускаться таким образом по уровням, слушая новости — дело весьма обычное; мы даже не всегда отдаем себе отчет в том, что сообщение на одном уровне прерывается. Наше подсознание следит за этим автоматически. Может быть, это так легко для нас потому, что уровни здесь сильно отличаются друг от друга. Если бы они были схожими, мы потеряли бы ориентацию в мгновение ока.
Пример более сложной рекурсии — наш Диалог. Ахилл и Черепаха присутствовали там на каждом из нескольких различных уровней. Иногда они читали историю, в которой сами были действующими лицами. Тут было легко запутаться, и приходилось напрягать все внимание, чтобы не потерять нить. «Так, посмотрим… настоящие Ахилл и Черепаха все еще наверху, в вертолете господина Удачи — вторичные сейчас находятся в картине Эшера — а теперь они нашли ту книгу и начали читать; значит, Ахилл и Черепаха, блуждающие по звуковым дорожкам „Маленького гармонического лабиринта“, — третичны. Стоп — я, кажется, пропустил один уровень…» Чтобы уследить за рекурсией в Диалоге, нам необходим сознательный мысленный стек, подобный такому, какой изображен ниже.
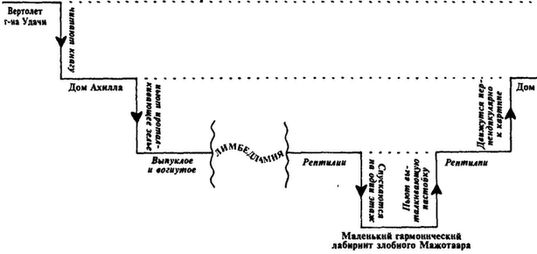
Рис. 26. Диаграмма структуры Диалога «Маленький гармонический лабиринт». Вертикальные спуски — проталкивание, подъемы — выталкивание. Обратите внимание, что диаграмма напоминает структуру абзацев в Диалоге. Из нее ясно следует, что угроза Удачи так никогда и не была выполнена — Ахилл и Черепаха остались висеть между небом и землей. Некоторые читатели, возможно, придут в отчаяние от этого недовытолкутого проталкивания, в то время как другие даже глазом не моргнут. В рассказе Баховский музыкальный лабиринт тоже был оборван слишком, скоро — но Ахилл не заметил в этом ничего особенного. Нарастающее напряжение почувствовала только Черепаха.
Стеки в музыке
Говоря о «Маленьком гармоническом лабиринте», мы должны обсудить следующую идею, которая косвенно упоминалась в диалоге: мы слушаем музыку рекурсивно — в частности, мы создаем мысленный стек ключей, и каждая новая модуляция проталкивает туда новый ключ. Если развить эту идею дальше, получится, что мы хотим услышать последовательность ключей в обратном порядке — выталкивая из стека ключи один за другим, пока не дойдем до основной тональности. Это, разумеется, преувеличение, но в нем есть доля правды. Слушая музыку, любой сколько-нибудь музыкальный человек автоматически создает минимальный стек с двумя ключами. В этом «коротком стеке» содержатся основная тональность, а также ближайший «псевдоключ», тональность, в которой композитор «находится» в данный момент. (Иными словами, самый общий и самый «местный» ключи. Таким образом слушатель знает, когда достигается тоника, и испытывает от этого сильное чувство «удовлетворения». В отличие от Ахилла, он также чувствует разницу между местным разрешением напряжения — например, разрешением в псевдотонику — и глобальным разрешением. Псевдоразрешение нагнетает напряжение, вместо того, чтобы его ослабить. Оно подобно иронической шутке — совсем как спасение Ахилла от ящериц, в то время как мы знаем, что на самом деле и он, и Черепаха все еще ожидают погибели от ножа месье Удачи.
Поскольку напряжение и разрешение — душа и сердце музыки, существует множество примеров на эту тему. Давайте взглянем на пару примеров из Баховской музыки. Бах написал много композиций в форме «ААББ»: обе части пьесы повторяются дважды. Возьмем джигу из «Французской сюиты #5», типичную для данной формы. Ее энергично введенная танцевальной мелодией тоника — «соль». Вскоре, однако, модуляция в части А вводит тесно связанную с первоначальной тональность «ре» (доминанта). Когда часть А кончается, мы находимся в тональности «ре». Может даже показаться, что пьеса заканчивается в ключе «ре»! (По крайней мере, так может подумать Ахилл.) Но тут случается странная вещь — мы внезапно прыгаем обратно к началу, снова в тональность «соль», и снова слышим тот же переход в «ре». Но тут случается странная вещь — мы внезапно прыгаем обратно к началу, снова в тональность «соль», и снова слышим тот же переход в «ре».
Затем следует часть Б. В результате тематического сдвига, мелодия здесь начинается с «ре», словно «ре» являлось тоникой с самого начала — но в конце концов, мелодия модулирует обратно в «соль»; это означает, что мы выталкиваемся обратно в тонику, и что часть Б оканчивается именно так, как надо. Тут случается это забавное повторение, отбрасывая нас, безо всякого предупреждения, назад к «ре», и затем возвращаясь к «соль» еще раз. Тут случается это забавное повторение, отбрасывая нас, безо всякого предупреждения, назад к «ре», и затем возвращаясь к «соль» еще раз.
Психологический эффект, достигаемый этими переходами, то внезапными, то плавными, трудно описать. Магия музыки отчасти и заключается в том, что мы способны автоматически уследить за этими переходами. А может быть, это магия Баха, сумевшего внести такую грацию в эту сложную структуру, что мы даже не замечаем, что именно там происходит.
Баховский «Маленький гармонический лабиринт» — это пьеса, в которой композитор пытается запутать слушателя быстрой сменой ключей. Вскоре вы настолько сбиты с толку, что совершенно теряете ориентацию. Вы не знаете, где настоящая тоника, если только у вас нет абсолютного слуха или вы, подобно Тезею, не прибегаете к помощи друга, который, словно Ариадна, дал бы вам нить, ведущую к началу. В данном случае, такой нитью являлись бы ноты. Эта пьеса, наряду с Естественно Растущим Каноном, показывает, что у нас, как у слушателей музыки, отсутствуют надежные глубокие стеки.
Рекурсия в языке
Наш интеллектуальный стек, пожалуй, более надежен для работы с языком. Грамматическая структура всех языков включает весьма сложные схемы для проталкивания в стек; трудность фразы, разумеется, возрастает с количеством проталкиваний. Знаменитое немецкое явление «глагола-в-конце», о котором забавные истории о рассеянных профессорах, начинающих фразу, продолжающуюся все лекцию, и под завязку выдающих цепочку глаголов, в которой аудитория, давно потерявшая нить в этом стеке, не видит никакого смысла, часто рассказываются, представляет из себя прекрасный пример лингвистического проталкивания и выталкивания. Замешательство в аудитории, которое неправильное выталкивание из стека, куда были сложены глаголы профессора, забавно вообразить, может произвести. Однако в повседневном немецком такие глубокие стеки почти никогда не встречаются; на самом деле, немцы частенько невольно нарушают правила, проталкивающие глагол в конец, с тем, чтобы избежать усилий, связанных с напряжением внимания в течение всей фразы. В любом языке имеются конструкции, где задействованы стеки, хотя обычно не такие впечатляющие, как в немецком. При этом всегда имеется возможность перефразировать предложение таким образом, чтобы уменьшить глубину стека.
Схемы рекурсивных переходов
Синтаксическая структура предложений хорошо подходит для метода описания рекурсивных схем и процессов — этот метод называется Схемой Рекурсивных Переходов (СРП). СРП представляет из себя диаграмму, показывающую различные пути для выполнения данного задания. Каждый такой путь состоит из нескольких узлов — маленьких квадратов, в которых что-то написано. Узлы соединены ребрами, или стрелками. Общее название данной СРП написано отдельно, слева от диаграммы, и в первом и последнем узле написано, соответственно, начало и конец. Остальные узлы содержат либо краткие инструкции, либо названия других СРП. Попав в определенный узел, вы должны либо выполнить указания, в нем написанные, либо перейти в указанную в нем СРП и работать уже там.
Возьмем простую СРП, под названием УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ, которая говорит нам, как создать определенную русскую фразу (см. рис. 27а) Двигаясь по схеме горизонтально, мы попадаем в начало, затем создаем прилагательное, затем — существительное, и затем приходим к концу. Например, «глупое мыло», или «неблагодарная закуска». Но ребра позволяют и другие возможности, например, повторить или совсем опустить прилагательное. Так мы можем сконструировать «молоко» или «огромная красная голубая зеленая зевота» и так далее.
Находясь в узле имя существительное, вы просите некий черный ящик под названием имя существительное выдать вам любое существительное с его склада. В компьютерной терминологии это называется процедурой вызова. Это означает, что вы временно передаете контроль некой процедуре (здесь, СУЩЕСТВИТЕЛЬНОМУ), которая 1) выполняет свою инструкцию (производит существительное) и 2) передает контроль вам обратно. В нашей СРП есть вызовы для двух таких процедур имя существительное и ИМЯ ПРИЛАГАТЕЛЬНОЕ. Обратите внимание, что СРП УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ может, в свою очередь, быть вызвана из какой-либо другой СРП — например, ПРЕДЛОЖЕНИЕ. В этом случае, схема УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ произвела бы «глупое мыло» и вернулась бы на свое место в предложении, откуда она была вызвана. Эта ситуация напоминает примеры со вложенными один в другой телефонными звонками или фрагментами новостей, где вы возвращаетесь к прерванному занятию.
Однако, хотя мы и назвали это «схемой рекурсивных переходов», мы еще не привели примера настоящей рекурсии.
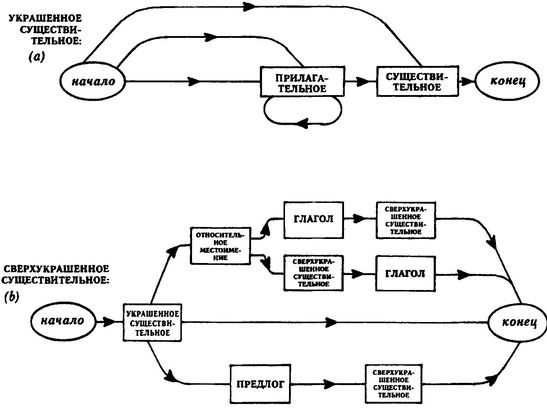
Ри. 27. Схема рекурсивных переходов для УКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО И СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО.
Рекурсия — и, по видимости, кругообразность — появляется тогда, когда мы переходим к такой СРП как СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ (Рис 27б). Как вы заметили, любая дорожка к СВЕРХУКРАШЕННОМУ СУЩЕСТВИТЕЛЬНОМУ проходит через узел УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ — таким образом, у нас обязательно появится какое-либо существительное. Мы можем на этом закончить и прийти к ФИНИШУ с «молоком» или «огромной красной голубой зеленой зевотой». Но остальные три пути к финишу сами включают рекурсивный вызов СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО. Это выглядит как порочный круг — определение чего-либо в терминах его самого. Действительно ли это происходит? На этот вопрос мы ответим так: «Да, но это не страшно.» Представьте, что в процедуре ПРЕДЛОЖЕНИЕ есть узел, вызывающий СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ, и мы попадаем именно в этот узел. Это означает, что мы прежде всего запоминаем (проталкиваем в стек) место этого узла внутри ПРЕДЛОЖЕНИЯ, чтобы знать, куда нам вернуться; после этого, мы переходим к самой процедуре СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ — мы должны найти способ его сконструировать. Предположим, что мы выбираем нижнюю из двух верхних дорожек:
УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ, ОТНОСИТЕЛЬНОЕ МЕСТОИМЕНИЕ, СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ, ГЛАГОЛ.
Итак, за дело: сначала мы выдаем «на-гора» УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ: «странные бублики»; затем, относительное местоимение: «которые»… теперь мы должны воспроизвести СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ — но ведь мы как раз и находимся в процессе создания СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО! Это верно, но вспомните наш пример с директором, которому позвонили в середине другого телефонного разговора. Он «отложил» первый разговор в стек и начал новую беседу так, словно ничего необычного не случилось. Давайте и мы сделаем так же.
Прежде всего запасемся обратным адресом: запишем в стек, в каком узле мы находились во время второго вызова СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО. Затем снова перейдем в начало схемы, словно ничего необычного не случилось. Теперь мы должны снова выбрать путь. Давайте, для разнообразия, попробуем пройти по нижней дорожке: УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ, ПРЕДЛОГ, СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ. Это значит, что сначала мы производим УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ (например, «пурпурная корова»), затем ПРЕДЛОГ (например, «без»)… и опять упираемся в рекурсию. Придется нам снова спуститься уровнем ниже — смотрите не споткнитесь! Чтобы избежать осложнений, давайте на этот раз выберем прямую дорогу. УКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ (например, «рога»). Этот вызов тут же попадает в узел КОНЕЦ, что позволяет нам вытолкнуться на предыдущий уровень. Мы обращаемся к стеку за обратным адресом, который отсылает нас к фразе «пурпурная корова без». Закончив дела на этом уровне и попав в узел КОНЕЦ, мы выталкиваемся еще раз. Теперь нам необходим ГЛАГОЛ (например, «слопала»). На этом вызов СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО на высшем уровне заканчивается. У нас получилась фраза:
«странные бублики, которые пурпурная корова без рогов слопала».
Когда мы вытолкнемся в последний раз, эта фраза будет передана наверх, к терпеливо ожидающей схеме ПРЕДЛОЖЕНИЕ.
Как видите, бесконечной регрессии не произошло, так как по крайней мере на одной из дорожек внутри СРП СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ мы не встретились с вызовом самого СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО. Конечно, мы могли бы упорствовать в выборе нижней дорожки внутри СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО — тогда бы нам никогда не удалось закончить работу, подобно тому, как нам не удалось полностью раскрыть сокращение БОГ. Однако если мы выбираем дорожки наугад, подобной бесконечной регрессии не случается.
«Спуск на дно» и гетерархии
Мы только что описали основные различия между круговыми и рекурсивными определениями — в последних всегда есть определенная часть без автореферентности. Таким образом, рано или поздно мы коснемся дна: наша цель — построение объекта, отвечающего определению — будет достигнута. Существуют и другие, менее прямые, чем самовызовы, пути для получения рекурсивности в СРП. Примером может служить картина Эшера «Рисующие руки» (рис. 135), где каждая процедура вызывает не саму себя, а другую. Например, можно представить СРП под названием ПРИДАТОЧНОЕ ПРЕДЛОЖЕНИЕ, вызывающую СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ, когда ей понадобится дополнение для переходного глагола — с другой стороны, высшая дорожка СВЕРХУКРАШЕННОГО СУЩЕСТВИТЕЛЬНОГО может вызывать ОТНОСИТЕЛЬНОЕ МЕСТОИМЕНИЕ и затем ПРЕДЛОЖЕНИЕ каждый раз, когда нам потребуется придаточное предложение. Это пример косвенной рекурсии; он напоминает двухступенчатую версию парадокса Эпименида.
Нет нужды говорить, что может существовать также трио процедур, вызывающих одну другую по кругу — и так далее. Может существовать даже целая семья СРП, спутанных между собой и что есть силы вызывающих друг друга и самих себя. Программа со структурой, в которой нет «высшего уровня» или «монитора», называется гетерархией (в отличие от иерархии). Этот термин изобретен Уорреном Мак Каллохом, одним из первых кибернетиков, посвятивших себя изучению мозга и интеллекта.
Расширение узлов
Есть также и другая возможность представить СРП графически. Каждый раз, когда, двигаясь по одной из дорожек, вы попадаете в узел, вызывающий другую СРП, вы «расширяете» этот узел, заменяя его на уменьшенную копию требуемой СРП (см. рис. 28). После этого вы приступаете к исполнению этой уменьшенной СРП.
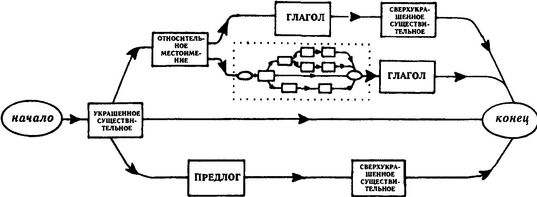
Рис. 28. СРП СВЕРХУКРАШЕННОЕ СУЩЕСТВИТЕЛЬНОЕ с одним рекурсивно расширенным узлом.
Выталкиваясь из расширенного узла, вы автоматически оказываетесь в нужном месте большой схемы. С другой стороны, находясь в маленькой схеме, вы можете конструировать внутри нее еще более миниатюрные СРП. Расширяя узлы по мере того, как вы в них попадаете, вы избегаете построения бесконечной схемы даже в том случае, когда СРП вызывает саму себя. Расширение узлов немного напоминает замену буквы в аббревиатуре на то слово, которое она представляет. Сокращение БОГ рекурсивно, но его дефект — или преимущество — заключается в том, что мы должны все время расширять букву «Б» и, таким образом, она никогда не достигнет «дна». Однако когда СРП является частью настоящей компьютерной программы, в ней всегда есть по крайней мере одна дорожка, избегающая как прямой, так и косвенной рекурсивности. Поэтому бесконечного регресса там не бывает. Даже самая гетерархическая программа рано или поздно заканчивается — иначе она вообще не работала бы! Она продолжала бы расширять узлы один за другим до скончания веков.
Диаграмма G и рекурсивные ряды
Бесконечные геометрические структуры могут быть определены именно так-как расширение узлов один за другим. Давайте попробуем определить бесконечную диаграмму — назовем ее «диаграммой G». Воспользуемся следующим условным обозначением, в двух узлах напишем просто букву «G», которая, однако, будет представлять всю диаграмму G. На рис. 28 показана диаграмма G, использующая такую условную нотацию. Если мы захотим представить эту диаграмму более явно, мы должны расширить каждый узел, обозначенный буквой G, то есть заменить его на уменьшенную копию той же диаграммы G (см. рис. 29 б). Эта версия диаграммы G «второго порядка» дает нам некоторое представление о том, как бы выглядела конечная, невыполнимая диаграмма G. На рис. 30 показана большая часть диаграммы G; все узлы пронумерованы снизу вверх и слева направо. Внизу добавлены два дополнительных узла под номерами 1 и 2. У этого бесконечного «дерева» есть некоторые весьма интересные математические свойства. Двигаясь по нему справа налево, мы получаем знаменитый ряд чисел Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Этот рад был открыт в 1202 году Леонардом из Пизы, сыном Боначчи — отсюда Филиус Боначчи или, сокращенно, Фибоначчи.
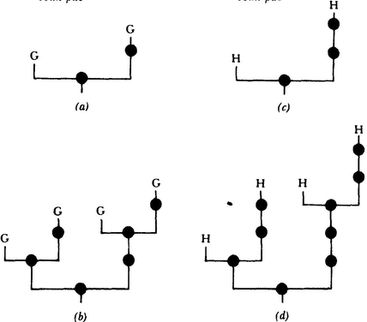
Рис. 29. а) Диаграмма G, нерасширенная; б) Диаграмма G, расширенная один раз; в) Диаграмма H, нерасширенная; г) Диаграмма H, расширенная один раз один раз
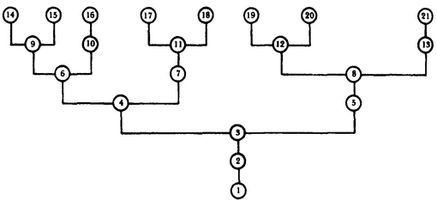
Рис. 30. Диаграмма G, расширенная далее. Узлы пронумерованы.
Это числа описываются рекурсивно при помощи следующей пары формул:
FIBO (n) = FIBO (n — 1) + FIBO (n — 2) for n > 2
FIBO (n) = FIBO (2) = 1

Рис. 31. СРП для чисел Фибоначчи
Таким образом, вы можете вычислить ФИБО(15) с помощью ряда рекурсивных вызовов описанной в этой схеме процедуры. Это рекурсивное определение касается дна, когда вы доходите до явно выраженных ФИБО(1) и ФИБО(2). Для этого надо пройти по схеме назад, к меньшим и меньшим значениям n. Пятиться раком довольно неудобно, вместо этого можно начать с ФИБО(1) и ФИБО(2) и идти вперед, складывая два предыдущих числа, пока вы не получите ФИБО(15). Так вам не придется следить за стеком.
Но это еще не самое интересное свойство диаграммы G! Ее структура может быть целиком закодирована в следующем рекурсивном определении.
G(n) = n-G(G(n-1)) для n>0
G(0) = 0
Каким образом эта формула G(n) отражает структуру дерева? Очень просто: если вы начнете строить дерево, помещая G(n) под n для всех значений n, у вас получится диаграмма G. На самом деле, именно так я и открыл эту диаграмму. Я занимался исследованием функции G; однажды, пытаясь ускорить вычисления, я решил представить уже имеющиеся у меня значения в форме дерева. К моему удивлению оказалось, что это дерево обладает очень аккуратной геометрической рекурсивностью.
Еще более занимательным получается аналогичное дерево для функции H(n), имеющей на одно рекурсивное вложение больше, чем G:
H(n) = n - H(H(H(n-1))) для n>0
H(0) = 0
Таким образом, соответствующая диаграмма H косвенно определяется так, как показано на рис. 29 в). Правая ветвь отличается от G только тем, что в ней на один узел больше. И так далее, для любого количества вложений. Рекурсивные геометрические структуры проявляют замечательную регулярность, в точности соответствующую рекурсивным алгебраическим определениям.
Вопрос для любознательных читателей: представьте себе, что вы перевернули диаграмму G так, что у вас получилось ее зеркальное отображение. Номера узлов нового дерева возрастают теперь слева направо. Можете ли вы найти рекурсивное алгебраическое определение для такого «дерева-перевертыша»? Как насчет определения для перевертыша дерева H? И так далее?
Другая забавная задача включает пару рекурсивно сплетенных функций F(n) и M(n) — так сказать, супружеская парочка функций — определенных следующим образом:
F(n) = n-M(F(n-1))
для n>0
M(n) = n-F(M(n-1))
F(0) = 1, M(0) = 0
СРП для этих двух функций вызывают как друг друга, так и самих себя. Задача состоит в том, чтобы найти рекурсивные структуры диаграмм M и F. Они весьма просты и элегантны.
Хаотическая последовательность
Последний пример рекурсии в теории чисел приводит к небольшой загадке. Рассмотрим следующее рекурсивное определение функции.
Q(n) = Q(n-Q(n-1)) + Q(n-Q(n-2) для n>2
Q(1) = Q(2) = 1
Это напоминает определение Фибоначчи тем, что каждое новое значение является суммой двух предыдущих значений — но не ближайших! Вместо этого, два ближайших предыдущих значения указывают нам, насколько далеко мы должны отступить, чтобы найти числа, которые надо сложить для получения нового значения. Вот первые семнадцать чисел Q.

Чтобы получить следующее число, надо продвинуться налево (считая от многоточия), соответственно, на 9 и 10 шагов; вы получите 5 и 6 (отмеченные стрелками). Их сумма — 11 — и дает новое значение: Q(18). Странный процесс: список уже известных чисел Q используется для расширения самого ряда. Получающаяся последовательность, мягко выражаясь, беспорядочна, и чем дальше мы продвигаемся, тем бессмысленнее она кажется. Это один из тех странных случаев, когда естественное определение приводит к весьма странному результату — хаос, полученный упорядоченным способом. При этом возникает вопрос: нет ли в кажущемся хаосе какого-то скрытого порядка? Разумеется, из определения следует, что некий порядок существует. Но интересно, есть ли иной способ определить данный ряд — если повезет, нерекурсивно?
Два удивительных рекурсивных графика
Чудес рекурсии в математике множество, и я не собираюсь здесь говорить о них подробно. Я остановлюсь лишь на двух особо интересных случаях с которыми мне пришлось столкнуться. Речь пойдет о двух графиках. Один из них — часть моих исследований по теории чисел. Другой возник в процессе моей работы над докторской диссертацией по физике твердых тел. Особенно поразительно то, что эти графики находятся в родстве между собой.
Первый (рис. 32) — график функции, которую я называю INT (x). Здесь она дана для x между 0 и 1. Чтобы найти x между любой другой парой чисел n и n+1, вы должны вычислить INT (x-n) и затем снова прибавить n. Как видите, структура этого графика прерывиста. Она состоит из бесконечного числа изогнутых кусочков, уменьшающихся ближе к краям. Если вы посмотрите на любой такой кусочек попристальнее, вы увидите, что перед вами — копия целого графика, только слегка изогнутая! Последствия этого удивительны; одним из них является то, что график INT состоит исключительно из копий себя самого, вложенных одна в другую до бесконечности. Если вы возьмете любую, сколь угодно малую часть графика, у вас окажется полная копия всего графика — на самом деле, бесконечное количество таких копий!
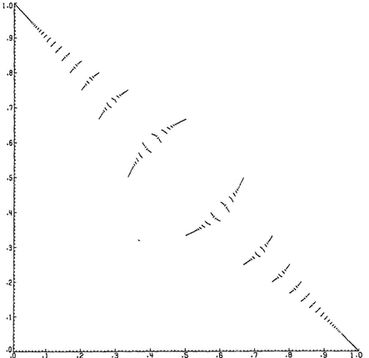
Рис. 32. График функции INT(x). В точках рациональных значений x функция прерывается.
Вы можете подумать, что INT слишком эфемерна, чтобы существовать в действительности, поскольку она состоит лишь из копий самой себя. Ее определение выглядит слишком круговым.
Как начинается эта функция? Где ее «исток»? Это очень интересный вопрос. Важно отметить, что, описывая INT человеку, никогда не видевшему графика этой функции, недостаточно просто сказать, что она состоит из копий себя самой. Вторая, нерекурсивная часть описания должна содержать сведения о том, где эти копии лежат внутри графика и каким образом они деформированы по отношению к нему. Только взятые вместе, эти два аспекта INT определяют ее структуру. Точно так же, чтобы определить числа Фибоначчи, нам понадобились две строчки — одна, определяющая рекурсию, и другая, определяющая дно — первоначальные значения функции. Приведу конкретный пример: если вы замените одно из двух первоначальных значений на 3 вместо 1, то получите совершенно иную последовательность, известную под названием ряда Лукаса:

В определении INT «дну» соответствует рисунок (рис. 33а), состоящий из множества квадратов, указывающих, где находятся копии и каким образом они деформированы. Я называю это «скелетом» INT. Чтобы построить INT на основе скелета, вы должны действовать следующим образом. Сначала для каждого квадрата надо проделать две операции: (1) вложите туда уменьшенную и изогнутую копию скелета, следуя направлению изогнутой линии внутри; (2) сотрите квадрат-рамку и линию внутри него. Закончив этот процесс для каждого квадрата первоначального скелета, вы получите вместо одного большого скелета множество скелетов-«деток». Теперь тот же процесс повторяется уровнем ниже, для каждого скелета-детки. Затем то же самое повторяется еще раз, и еще, и еще… В пределе вы приближаетесь к точному графику INT, хотя никогда его не достигаете. Снова и снова вкладывая скелет графика внутрь себя самого, вы постепенно строите график «из ничего». Но, по сути, «ничто» не было таковым — оно было рисунком.

Рис. 33 а. Скелет, на базе которого путем рекурсивной замены строится INT.
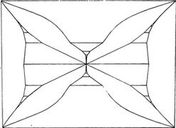
Рис. 33 б. Скелет, на базе которого путем рекурсивной замены строится график G.
Поясним сказанное на еще более впечатляющем примере: вообразите, что вы оставляете рекурсивную часть определения INT, но заменяете начальный рисунок, скелет. Вариант скелета показан на рис. 33б); также и здесь квадраты уменьшаются ближе к углам. Если вы начнете вкладывать этот скелет в себя самого снова и снова, вы получите основной график моей докторской диссертации, который я назвал Графиком G (рис. 34). (На самом деле, там также потребовались определенные сложные деформации, но основной идеей остается «самовложение».) Таким образом, График G — член семьи INT. Это дальний родственник, так как его скелет намного сложнее скелета INT; однако рекурсивные части их определений идентичны, и именно в этом заключается их родство.
Я не буду слишком долго держать вас в неведении относительно происхождения этих замечательных графиков. INT (сокращенное interchange — обмен) связан с проблемой непрерывных дробей, а еще точнее — «последовательностей ETA». В основе INT лежит идея о том, что знаки плюс и минус взаимозаменяемы для определенного вида непрерывных дробей. Отсюда следует то, что INT(INT(x))=x. Когда x рационально, ITN(x) также рациональна; квадратичные значения x дают квадратичные значения INT(x). He знаю, верна ли эта тенденция для высших алгебраических степеней. Другим любопытным свойством INT является то, что в точках рациональных значений x функция разрывается скачками, в то время как в точках иррациональных значений x она непрерывна.

Рис. 34. График G: рекурсивный график, показывающий энергетические полосы для электронов в идеализированном кристалле, помещенном в магнитное поле. a, представляющая силу магнитного поля, изменяется вертикально от 0 до 1.Энергия показана на горизонтальной оси. Сегменты горизонтальных линий — разрешенные энергии электронов.
График G представляет собой сильно упрощенный ответ на вопрос «Какую энергию может иметь электрон в кристалле, помещенном в магнитное поле?» Это очень интересная проблема, так как она совмещает две фундаментальные физические ситуации: электрон в совершенном кристалле и электрон в однородном магнитном поле. Решения этих простых проблем хорошо известны и кажутся почти несовместимыми; тем интереснее выяснить, как природе удается их совместить. Оказывается, что ситуации «электрон в кристалле без магнитного поля» и «электрон в магнитном поле без кристалла» все-таки имеют одну общую черту: в обоих случаях электрон ведет себя периодично во времени. Когда две ситуации совмещаются, отношение их периодов является ключевым параметром, так как оно выражает возможные уровни энергии электронов. Однако свой секрет это отношение выдает только тогда, когда оно записано в форме непрерывной дроби.
График G показывает это распределение. Горизонтальные оси представляют энергию, вертикальные — упомянутое выше отношение временных периодов, которое мы называем «а». Внизу а равняется нулю, наверху — единице. Когда а равняется нулю, магнитное поле отсутствует. Каждый из составляющих график G сегментов — энергетическая полоса, представляющая возможные уровни энергии. Каждая из разномасштабных пустых полос, пересекающих график G, представляет районы запрещенных энергий. Одним из самых удивительных свойств графика G является то, что когда а рациональна (иными словами, может быть представлена в форме p/q), то существует ровно q таких пустых полос (хотя, когда q четно, две из них «целуются» в центре).
Когда а иррационально, полосы сжимаются до точек, бесконечное число которых разбросано по так называемому «множеству Кантора» — еще один рекурсивно определяемый объект, берущий начало в топологии.
У читателя может возникнуть вопрос, можно ли получить такую сложную структуру экспериментальным путем. Честно говоря, я бы сам удивился больше всех, если бы в результате какого-нибудь эксперимента получился График G. График G «физичен» в том смысле, что он указывает, как можно математически подходить к менее идеальным физическим проблемам. Другими словами, График G принадлежит к области теоретической физики, а не указывает физикам-практикам на то, что они могут получить в результате экспериментов. Как-то раз один из моих друзей-агностиков, пораженный бесконечным количеством бесконечностей Графика G, именовал этот график «портретом Бога» — и это совсем не показалось мне богохульством.
Рекурсия на низшем уровне материи
Мы уже встретились с рекурсией в грамматике языков, видели рекурсивные геометрические деревья, тянущие свои ветви в бесконечность, и привели пример рекурсии в физике твердых тел. Теперь давайте взглянем еще на один способ рекурсивного устройства мира. Я имею в виду элементарные частицы: электроны, протоны, нейтроны и крохотные кванты электромагнитного излучения, называемые «фотонами». Мы увидим, что эти частицы в некотором роде «вставлены» друг в друга (это определено со всей строгостью только в релятивистской квантовой механике), и что это положение можно описать рекурсивно — может быть, даже с помощью какой-либо «грамматики».
Начнем с того, что если бы элементарные частицы не взаимодействовали друг с другом, мир был бы невероятно прост. В таком мире физики были бы наверху блаженства, так как там они могли бы с легкостью вычислить поведение всех частиц! (Конечно, при условии, что в таком мире существовали бы сами физики — что кажется весьма сомнительным.) Невзаимодействующие частицы называются голыми, и являются чисто гипотетическими — в реальном мире их не существует.
Теперь представьте себе, что мы «включаем» взаимодействия — частицы связываются между собой так же, как связаны между собой функции M и F или женатые пары. Эти реальные частицы называются ренормализованными — неуклюжий, но интересный термин. Теперь каждая частица определяется через совокупность всех других частиц, которые, в свою очередь, определяются через первую частицу, и так далее. Получается движение кругом и кругом, по бесконечной петле.
Давайте теперь перейдем на более конкретные темы и ограничимся двумя частицами — электронами и фотонами. Нам также придется включить сюда и античастицу электрона — позитрон. (Фотон является античастицей себя самого.) Вообразите себе скучный мир, в которой голый электрон желает добраться от точки А до точки В, как Зенон в моей «Трехголосной инвенции».
Физик нарисовал бы такую картину:

Существует весьма простое математическое выражение, соответствующее этому отрезку и его конечным точкам. С его помощью, физик может понять поведение голого электрона на этой траектории.
Теперь давайте «включим» электромагнитное взаимодействие, так что электроны и фотоны начнут взаимодействовать. Хотя в этой сцене фотоны не участвуют, наше допущение будет иметь серьезные последствия даже для этой простой траектории. В частности, электроны теперь способны испускать и снова поглощать виртуальные фотоны — фотоны, рождающиеся и умирающие прежде, чем их заметят. Этот процесс выглядит так:

По мере того, как электрон распространяется, он может испускать и снова поглощать один фотон за другим, иногда вкладывая один фотон в другой, как показано на рисунке ниже:

Математические выражения, соответствующие этим диаграммам — так называемым «диаграммам Файнмана» — легко записать, но труднее вычислить, чем соответствующие выражения для голых электронов. Самое сложное то, что фотон — реальный или виртуальный — может на мгновение превратиться в пару электрон-позитрон. Между ними происходит аннигиляция, и, как по волшебству, первоначальный фотон появляется снова! Этот процесс показан на рисунке ниже:
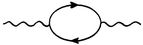
Стрелка, указывающая направо, — электрон, налево — позитрон. Как вы, наверно, догадались, эти виртуальные процессы могут вставляться один в другой до любой глубины. В результате может получиться довольно сложная диаграмма, такая, как показана на рис. 35. На данной диаграмме Файнмана один электрон входит слева в точке А, и после серии удивительных акробатических трюков выходит справа в точке В. Отсюда видно, что линии как электрона, так и фотона могут быть сколько угодно «украшены». Такую диаграмму чрезвычайно трудно вычислить.

Рис. 35. Диаграмма Файнмана. показывающая распространение ренормализованного электрона от А до В. Время возрастает слева направо, это значит, что в тех местах, где стрелка указывает справа налево, электрон движется «обратно во времени». Или, говоря более интуитивно, антиэлектрон(позитрон) движется вперед во времени. Фотоны — свои собственные античастицы, и поэтому их линии не нуждаются в стрелках
У этих диаграмм своя «грамматика», позволяющая воплотиться в жизнь только определенным картинкам. Например, ситуация, изображенная ниже, невозможна:

Вы можете возразить, что это не является «правильно-сформированной» диаграммой Файнмана. Грамматика, о которой мы говорим, берет начало в основных законах физики, таких, как сохранение энергии, сохранение заряда, и т. д. Подобно грамматикам человеческих языков, эта грамматика рекурсивна — в ней возможны структуры, вставленные одну в другую. Можно было бы нарисовать серию схем рекурсивных переходов, определяющих «грамматику» электромагнитных взаимодействий.
Когда голые электроны и голые фотоны вступают в подобные сложные, запутанные взаимодействия, результатом являются ренормализованные электроны и фотоны. Таким образом, чтобы понять, каким образом реальный, физический электрон распространяется от А до В, физик должен найти что-то вроде среднего арифметического для бесконечного множества всех возможных графиков, включающих виртуальные частицы. Что это, если не дзен-буддизм, да еще в превосходной степени?…
Таким образом, физическая — ренормализованная — частица включает (1) голую частицу и (2) путаницу виртуальных частиц, сложнейшим рекурсивным образом связанных между собой. Значит, существование каждой реальной частицы включает существование бесконечного множества других частиц, содержащихся в виртуальном «облаке», окружающем эту частицу, когда она движется. И, разумеется, каждая из виртуальных частиц в облаке несет с собой свое собственное виртуальное облако — и так далее, до бесконечности.
Физики, изучающие элементарные частицы, не в состоянии справиться с подобной сложностью; чтобы понять поведение электронов и фотонов, они используют приближения, принимающие во внимание только самые простые диаграммы Файнмана. К счастью, чем сложнее диаграмма, тем меньше ее значимость. Никто не знает, каким образом можно учесть все бесконечное множество возможных диаграмм, чтобы описать поведение полностью ренормализованного физического электрона. Однако, рассматривая сотни простейших диаграмм некоторых процессов, физики смогли правильно предсказать одну из величин (так называемый g-фактор муона) с точностью до девяти знаков!
Ренормализация происходит не только среди электронов и фотонов. Физики используют идею ренормализации каждый раз, когда они пытаются понять поведение любых взаимодействующих частиц. Так что протоны и нейтроны, нейтрино, пи-мезоны, кварки — все звери этого субатомного зверинца — все имеют голые и ренормализованные версии в физических теориях. И из миллиардов этих пузырей в пузырях состоят все штуковины и чепуховины мира.
Копии и схожесть
Давайте теперь снова взглянем на График G. Возможно, читатель помнит, что во введении мы говорили о разных формах канонов. Каждый тип канона использовал основную тему и копировал ее с помощью изоморфизма, или сохраняющей информацию трансформации. Иногда копии получались вверх ногами, иногда задом наперед, а иногда растянутые или сокращенные… В Графике G есть все эти типы трансформации, и даже больше. Отображение всего графика в его частях требует изменения размеров, искажения, отражения и так далее. И все же мы можем говорить о некоей основной тождественности, которую при определенном усилии можно заметить — особенно, если ваш глаз уже натренирован на INT.
Эшер использовал идею о частях объекта, являющихся копией самого этого объекта, в своей гравюре на дереве «Рыбы и чешуйки» (Рис. 36). Конечно, эти рыбы и чешуйки схожи только в том случае, если мы рассматриваем картину на достаточно абстрактном уровне. Каждый знает, что рыбьи чешуйки — вовсе не уменьшенные копии самой рыбы, так же как и клетки рыбы не являются ее крохотными копиями. Однако ДНК, содержащаяся в каждой из рыбьих клеток, и есть, в действительности, сильно уменьшенная «копия» самой рыбы — таким образом, гравюра Эшера правдивее, чем кажется.

Рис. 36. М. К. Эшер. Рыбы и чешуйки. (Гравюра на дереве, 1959).
Что именно делает всех бабочек «похожими» друг на друга? Отображение одной бабочки на другую не совпадает по клеткам; скорее, оно совпадает по функциональным органам, отчасти на макроскопическом и отчасти на микроскопическом масштабе. Вместо точных пропорций сохраняются функциональные отношения частей. Именно этот тип изоморфизма связывает между собой бабочек на гравюре Эшера «Бабочки» (рис. 37). То же верно и для более абстрактных бабочек Графика G, связанных между собой математическими отображениями одной функциональной части в другую. При этом полностью игнорируются пропорции линий, углы, и тому подобное.

Рис. 37. М. К. Эшер. «Бабочки» (гравюра на дереве, 1950).
Перенося это исследование схожести на еще более высокий уровень абстракции, мы можем спросить: «Что же делает схожими все картины Эшера?» Было бы смешно пытаться отобразить их, часть за частью, одну на другую. Удивительно то, что ответ содержится даже в самом крохотном фрагменте картины Эшера или композиции Баха. Подобно тому, как ДНК рыбы содержится внутри самого малюсенького кусочка этой рыбы, авторская «подпись» содержится в самом маленьком кусочке его произведения. Для этого явления у нас нет другого обозначения, кроме расплывчатого и ускользающего понятия «стиля». Мы снова и снова сталкиваемся со «схожестью-внутри-различия» и с вопросом:
Когда два предмета схожи между собой?
В этой книге мы вернемся к нему еще не раз и, рассмотрев его под всевозможными углами, увидим, насколько такой простой вопрос связан с природой разума. То, что этот вопрос возник в главе, посвященной рекурсии, не случайно, рекурсия — это область, в которой схожесть-внутри-различия играет центральную роль. Рекурсия основана на «одном и том же» событии, происходящем одновременно на нескольких различных уровнях. При этом события на разных уровнях не одинаковы — скорее мы находим в них какую-либо общую черту, как бы они не различались. Например, в «Маленьком гармоническом лабиринте» истории на разных уровнях весьма отличны друг от друга, и их схожесть заключается лишь в двух фактах: (1) все они — истории и (2) во всех историях действуют Ахилл и Черепаха. В остальном, эти истории радикально отличаются одна от другой.
Программирование и рекурсия: модульность, петли, процедуры
Одна из основных способностей, необходимых в компьютерном программировании, — это умение заметить, когда два явления схожи в широком смысле, поскольку это ведет к модуляризации — разбиванию задачи на несколько естественных подзадач. Представьте, например, что вам надо исполнить одну за другой серию схожих операций. Вместо того, чтобы записывать каждую из них, мы можем написать петлю (или цикл), которая говорит компьютеру, что, выполнив некое множество операций, он должен вернуться к началу и повторять тот же процесс снова и снова, пока не будет выполнено некое условие. Тело петли — определенные повторяющиеся команды — не должно быть жестко установленным; в нем допустимы предсказуемые вариации. Примером может служить несложная проверка того, является ли число N простым. Вначале вы делите число N на 2, потом на 3, 4, 5, и так далее, до N-1. Если N не делится ни на одно из этих чисел, то N — простое число.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
1.3. Методология исследования элементов структуры техники и анализ параметров структуры прогресса
1.3. Методология исследования элементов структуры техники и анализ параметров структуры прогресса Проблема открытия, рационализации, изобретения как форм умственной деятельности интеллектуальных систем (И.С. Ладенко), лейтмотивом функционального поведения которых
Глава 5. Апокалипсис у ворот, или в 1968-м году структуры расхаживали по улицам — повторится ли такое?
Глава 5. Апокалипсис у ворот, или в 1968-м году структуры расхаживали по улицам — повторится ли такое? Название, конечно же, связано с реакцией Лакана на хорошо известное антиструктуралистское граффити на парижских стенах 1968- го года: «структуры не разгуливают по улицам»,
Глава вторая. Всеобщие структуры чистого сознания
Глава вторая. Всеобщие структуры чистого сознания § 76. Тема последующих изысканий Через посредство феноменологической редукции все царство трансцендентного сознания выявилось для нас как царство бытия в определенном смысле «абсолютного». Вот изначальная категория
АВТОКОММУНИКАЦИОННЫЕ ПРОЦЕССЫ
АВТОКОММУНИКАЦИОННЫЕ ПРОЦЕССЫ АВТОКОММУНИКАЦИОННЫЕ ПРОЦЕССЫ (гр. autos - сам, само- и лат. communicatio - разговор; букв, "общение, разговор с самим собой") - одна из основных культурных моделей коммуникации (см. Коммуникация), в которой сообщение передается по каналу "Я - Я", т.е. сам
2. Межпредельные, или внутрипредельные, то есть промежуточные, структуры, или структуры в собственном смысле слова
2. Межпредельные, или внутрипредельные, то есть промежуточные, структуры, или структуры в собственном смысле слова Ясно, что такого рода структуры как раз и являются теми структурами, как они обычно понимаются. Однако здесь должна быть соблюдаема та античная специфика,
Глава 1 ОБЗОР СТРУКТУРЫ ВСЕЛЕННОЙ. ИСХОДНЫЕ ПОСТУЛАТЫ
Глава 1 ОБЗОР СТРУКТУРЫ ВСЕЛЕННОЙ. ИСХОДНЫЕ ПОСТУЛАТЫ Общая краткая схема структуры виртуальной вселенной выглядит следующим образом: Определение: Ядро – это центральный вычислитель виртуальной вселенной. Он вычисляет все изменения, происходящие «сами собой» (то есть
Глава 2 ПРОЦЕССЫ УПРАВЛЕНИЯ ТЕЛОМ
Глава 2 ПРОЦЕССЫ УПРАВЛЕНИЯ ТЕЛОМ Люди, живущие на Земле, обычно, так или иначе, играют в игру в управление своим телом. В самом управлении телом нет ничего плохого, – управление телом должно быть исключительно совершенным, – но игра в управление…Игра, то есть
Глава 4 ПРОЦЕССЫ ЭНЕРГИИ
Глава 4 ПРОЦЕССЫ ЭНЕРГИИ Несмотря на «помпезное» название этой группы процессов, они имеют дело просто с эмоциями ИО.Начав играть в игры с эмоциями, ИО может прийти к тому, что рассеет энергию разума на всякие разные мелочи, – например, на сдерживание игр с эмоциями типа
Глава 6 ТЕЛЕСНО-ОРИЕНТИРОВАННЫЕ ПРОЦЕССЫ
Глава 6 ТЕЛЕСНО-ОРИЕНТИРОВАННЫЕ ПРОЦЕССЫ В начале этой главы я, к сожалению, не удержался от «наезда». По ходу изложения главы желание наезжать прошло, а написанный текст остался. Но, почему бы не дать его Вам в первоначальном виде? Итак, читайте, что
4. ПРОЦЕССЫ
4. ПРОЦЕССЫ Первые два процесса – это процессы из серии «Надень на себя свое тело». Они направлены на восстановление общения ИО со всем телом.4.1. Почувствуй прикосновениеТеория: Каждая конкретная психосоматическая болезнь происходит от неудачи в налаживании общения с
Параллельные процессы
Параллельные процессы Во второй половине ХХ века происходят удивительные параллельные процессы. С одной стороны, евгеника мутирует в генетику. А, с другой, происходят удивительные превращения самой Американской цивилизации, равно как и всего Западного мира.До Второй