Комплексные числа

Комплексные числа

Оказывается, что действительные числа — это не единственная математически мощная и изящная система чисел. Система действительных чисел все же не лишена некоторых неудобств. Например, квадратные корни можно извлекать только из положительных чисел (или нуля), но никак не из отрицательных чисел. С математической точки зрения — и отвлекаясь пока что от вопроса о непосредственной связи с физическом миром — было бы очень удобно иметь возможность извлекать квадратные корни как из положительных, так и из отрицательных чисел. Давайте постулируем существование, или попросту «изобретем» квадратный корень из числа -1. Обозначим его буквой i. Тогда мы имеем:

i ² = -1.

Величина i, конечно же, не может быть действительным числом, поскольку произведение действительного числа на самого себя всегда положительно (или равно нулю, если само число равно нулю). Поэтому числа, квадраты которых отрицательны, обычно называют мнимыми. Следует, однако, отметить, что эти «мнимые» числа не менее реальны, чем ставшие уже привычными «действительные» числа. Как я уже отмечал выше, связь таких «действительных» чисел с физической реальностью далеко не столь непосредственна и убедительна, как может показаться на первый взгляд, и основана на математической идеализации о допустимости бесконечного уточнения, которая не имеет ясного априорного обоснования в природе.

Имея квадратный корень из -1, можно без особого труда получить квадратные корни для всех действительных чисел. Если а является положительным действительным числом, то величина i х ?a есть квадратный корень из отрицательного действительного числа — а. (У этого числа есть еще другой квадратный корень, а именно — i х ?а.) Ну, а что же можно сказать о самом числе i ? Есть ли у него квадратный корень? Разумеется есть, поскольку, как легко проверить, величина

1+i /?2

(равно как и та же величина, взятая с отрицательным знаком), будучи возведена в квадрат, равна i. А у этой величины, в свою очередь, есть квадратный корень? Ответ опять положительный: квадрат числа

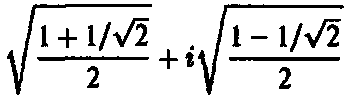 или того же числа, взятого с отрицательным знаком, действительно равен (1 + i)/?2.

Обратите внимание, что при образовании такого рода величин мы позволили себе складывать действительные и мнимые числа, а также умножать наши числа на произвольные действительные числа (или делить их на произвольные ненулевые действительные числа, а это то же самое, что умножать их на обратные величины). Получаемые таким образом объекты называются комплексными числами. Комплексное число это число вида: а + ib, где а и b — это действительные числа, называемые, соответственно, действительной и мнимой частью комплексного числа. Правила сложения и умножения двух таких чисел вытекают из обычных правил (школьной) алгебры с одним дополнительным правилом i ² = — 1:

(а + ib) + (с + id) = (а + с) + i(b + d),

(а + ib) х (с + id) = (ас — bd) + i(ad + bc).

Удивительное дело: к созданию этой системы чисел нас подтолкнуло желание иметь возможность извлечения квадратных корней из любых чисел. Эта цель достигнута, хотя само по себе это еще не очевидно. Но новая система чисел позволяет делать гораздо больше: безнаказанно извлекать кубические корни, корни пятой степени, корни девяносто девятой степени, корни ?-й степени, корни степени 1 + i и т. д. (это смог доказать еще в XVIII веке великий математик Леонард Эйлер). В качестве другого примера волшебных свойств комплексных чисел рассмотрим довольно сложные на вид тригонометрические формулы, которые проходят в школе. Так, синус и косинус суммы двух углов

sin (А + В) = sin A cos В + cos A sin В,

cos (А + В) = cos A cos В — sin A sin В

представляют собой, соответственно, просто-напросто мнимую и действительную части гораздо более простого (и легче запоминаемого!) комплексного уравнения[62]:

e ^iA+iB= e ^iA e ^iB

Все, что нам нужно здесь знать, это «формула Эйлера» (по-видимому, полученная за много лет до Эйлера замечательным английским математиком XVI века Роджером Котсом):

e ^iA= cosA+i sinA,

которую мы теперь подставим в приведенное выше уравнение. В результате имеем:

cos (А + B) + i sin (А + В) = (cosА + i sinA)(cosВ + i sinВ),

и, выполнив умножение в правой части, получим искомые тригонометрические соотношения.

Более того, любое алгебраическое уравнение

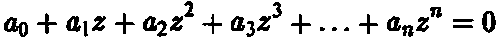
(где a₀, a₁, a₂….,a_n являются комплексными числами и a_n? 0) всегда имеет своим решением некоторое комплексное число z. Например, существует комплексное число, удовлетворяющее соотношению:

z¹⁰² + 999z³³ — ?z² = — 417 +i, хотя это совершенно не очевидно!

Это общее свойство иногда называют «основной теоремой алгебры». Многие математики XVIII века старались доказать этот результат. Получить удовлетворительное доказательство в общем случае оказалось не под силу даже Эйлеру. И только в 1831 году великий математик и естествоиспытатель Карл Фридрих Гаусс предложил потрясающий по своей оригинальности ход рассуждений и представил первое общее доказательство. Ключевым компонентом этого доказательства было применение топологических[63] рассуждений к геометрическому представлению комплексных чисел.

На самом деле Гаусс не был первым, кто использовал геометрическое представление комплексных чисел. Уоллис сделал то же самое примерно за двести лет до Гаусса, хотя далеко не столь результативно. Геометрическое представление комплексных чисел обычно связывают с именем Жана Робера Аргана — швейцарского бухгалтера, описавшего это представление в 1806 году, хотя полное описание этого представление было на самом деле дано девятью годами раньше норвежским геодезистом Каспаром Весселем. Согласно этой традиционной (хотя и не совсем правильной с исторической точки зрения) терминологии, я буду называть стандартное геометрическое представление комплексных чисел плоскостью Аргана.

Плоскость Аргана представляет собой обычную евклидову плоскость со стандартными декартовыми координатами x и y, где x обозначает расстояние по горизонтали (положительное вправо и отрицательное влево), а у — расстояние по вертикали (положительное вверху и отрицательное внизу). В этом случае комплексное число z = х + iy представляется точкой на плоскости Аргана с координатами (x, y) (рис. 3.8).

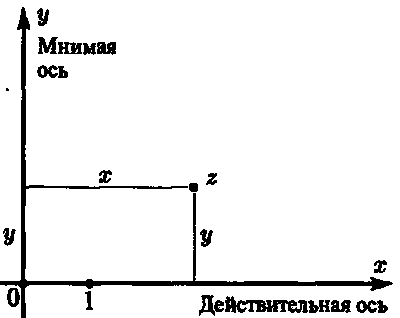
Рис. 3.8. Изображение комплексного числа z = х + iy на плоскости Аргана

Обратите внимание, что число 0 (рассматриваемое как комплексное число) соответствует началу координат, а число 1 — одной из точек на оси х.

Плоскость Аргана есть просто способ геометрически наглядной организации семейства комплексных чисел. Такое представление не является для нас чем-то совершенно новым. Мы уже знакомы с геометрическим представлением действительных чисел — в виде прямой линии, простирающейся на неограниченное расстояние в обоих направлениях. Одна из точек обозначена как 0, а еще одна — как 1. Точка 2 смещена относительно точки 1 равно настолько, насколько точка 1 смещена относительно точки 0; точка 1/2 расположена в точности посередине между точками 0 и 1; точка -1 расположена так, что точка 0 находится в точности посередине между точками -1 и 1, и т. д., и т. п. Отображенное таким образом множество действительных чисел называется действительной прямой. В случае комплексных чисел у нас есть уже целых два действительных числа — а и b — которые могут рассматриваться как координаты комплексного числа а + ib. Эти два числа дают нам две координаты точки на плоскости, в данном случае — на плоскости Аргана. Для примера я указал на рис. 3.9 приблизительные положения комплексных чисел

u = 1 + i 1,3, v = -2 + i, w = -1,5 — i 0,4.

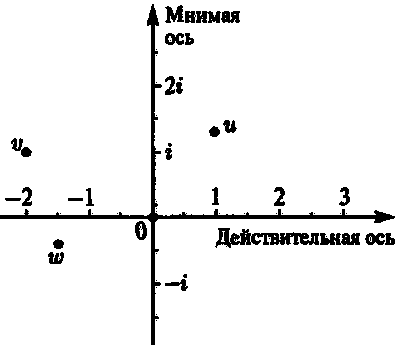
Рис. 3.9. Расположение чисел u = 1 + i1,3, v = -2 + i, ? = -1,5 — i0,4 на плоскости Аргана

Теперь основные алгебраические операции сложения и умножения комплексных чисел приобретают ясную геометрическую интерпретацию. Рассмотрим сначала сложение. Предположим, что u и v это два комплексных числа, представленные на плоскости Аргана в соответствии с описанной выше схемой. Тогда сумма этих двух чисел u + v представляется «векторной суммой» двух точек, то есть точка u + v находится на месте недостающей вершины параллелограмма, образованного точками u, v и началом координат 0. Нетрудно убедиться, что эта конструкция (рис. 3.10) действительно дает сумму двух чисел, но соответствующее доказательство я здесь опускаю.

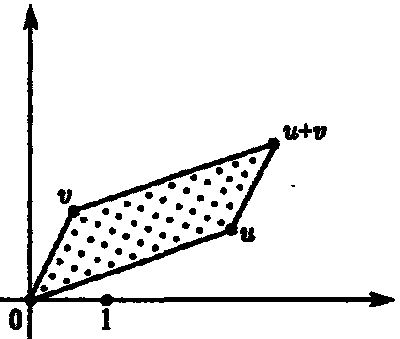
Рис. 3.10. Сумма u + v двух комплексных чисел определяется по правилу параллелограмма

Произведение uv двух комплексных чисел тоже имеет простую, хотя и, быть может, несколько менее очевидную геометрическую интерпретацию (рис. 3.11). (Я опять опускаю доказательство.)

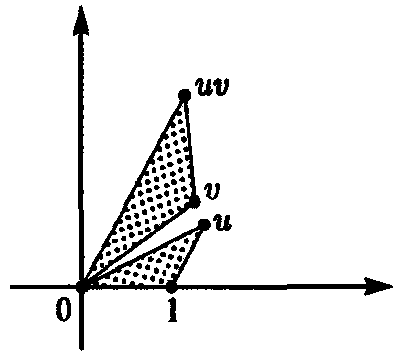
Рис. 3.11. Произведение uv двух комплексных чисел u и v — это такое число, что треугольник, образованный точками 0, v и uv, подобен треугольнику, образованному точками 0, 1 и u. То же самое можно сформулировать иначе: расстояние точки uv от 0 равно произведению расстояний от 0 до точек u и v, а угол между uv и действительной (горизонтальной) осью равен сумме углов между этой осью и отрезками к точкам и и v

Угол при начале координат между 1 и uv равен сумме углов между 1 и v и между 1 и u (все углы измеряются против часовой стрелки), а расстояние точки uv от начала координат равно произведению расстояний от начала координат до u и v. Это эквивалентно утверждению, что треугольник, образованный точками 0, v и uv подобен (и ориентирован подобно) треугольнику, образованному точками 0, 1 и u. (Энергичные читатели, не знакомые с такого рода построениями, могут сами убедиться в том, что эти построения непосредственно следуют из только что приведенных алгебраических правил сложения и умножения комплексных чисел, также как и упомянутые выше тригонометрические тождества.)

Данный текст является ознакомительным фрагментом.