§ 6. Исчисление суждений

§ 6. Исчисление суждений

Исчисление суждений изначально разрабатывалось как еще одна интерпретация символов, применяемых в теории классов. В определенной мере оба эти исчисления обладают тождественной формальной структурой, и каждое суждение в теории классов обладает соответствующим ему суждением в теории суждений, которое можно получить, используя подходящую интерпретацию. Приведенная ниже таблица может быть использована в качестве словаря для перевода теорем исчисления классов в теоремы исчисления суждений:

С помощью данного словаря все принципы, истинные относительно классов, могут быть сформулированы в иных символах и будут также истинны относительно суждений.

Несмотря на то что данный подход позволяет проявить формальные аналогии между двумя исчислениями, он, тем не менее, имеет несколько недостатков. Во-первых, как уже упоминалось, существует несколько теорем, которые являются истинными в случае, если термины обозначают суждения, и ложными, если они обозначают классы. Рассмотрим следующую теорему: если р имплицирует q или r, то р имплицирует q или р имплицирует r. Символически она записывается как [ p ? ( q ? r )] ? [( p ? q ) ? ( p ? r )] и является истинной для суждений. Однако если рассматривать ее применительно к классам, то она будет ложной. Например, неверно, что если все англичане являются либо мужчинами, либо женщинами, то все англичане являются мужчинами и все англичане являются женщинами.

Более серьезное возражение проистекает из того факта, что при разработке исчисления суждений мы хотим перечислить все используемые принципы вывода. Если мы будем развивать теорию суждений систематическим и дедуктивным образом, начиная с ряда недоказанных принципов для суждений, мы сможем доказать любой другой принцип. Если мы будем при этом достаточно осмотрительны, то сможем уберечь себя от опасности использования какого-либо принципа вывода, который мы не доказали бы ранее или не ввели в качестве допущения. Следовательно, действуя таким образом, мы можем достигнуть удовлетворительной систематизации логических принципов. Однако если мы используем исчисление классов в качестве основы для разработки теории суждений, то мы не сможем использовать данный метод получения всех принципов вывода.

Как и в исчислении классов, где все последние рассматривались относительно своих объемов, в исчислении суждений все суждения анализируются только относительно своих истинностных значений, а не относительно конкретного значения, которое в них утверждается. Читателю следует это четко уяснить, с тем чтобы не совершать грубых ошибок.

Проиллюстрируем сказанное на примере анализа определения термина «импликация», которое часто приводится в дискуссиях по символической логике, ( p ? q ) определяется как то, что эквивалентно ( p ? ? q ) или ( p . q ?)?. Словами: « p имплицирует q » истинно, если «

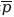
или q » истинно.

Но «

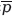
или q» истинно в любом из перечисленных случаев: 1) р истинно и q истинно; 2) р ложно и q ложно; 3) р ложно и q ложно. Единственное, что может сделать данное суждение ложным, это ситуация, в которой р является истинным, a q ложным. Из этого следует, что «р имплицирует q» истинно в любом из первых трех перечисленных случаев. Однако если мы рассмотрим данные случаи подробнее, то должны будем признать, что до тех пор пока р ложно, «р имплицирует q» будет истинным безотносительно того, истинно или ложно q; и до тех пор, пока q истинно, «р имплицирует q» будет истинным безотносительно того, истинно или ложно р. Все это можно сформулировать несколько парадоксальным образом, сказав, что ложное суждение имплицирует любое суждение и что любое суждение имплицирует истинное суждение. Следовательно, каждое из следующих суждений должно быть истинным: «„2 + 2 = 5" имплицирует „Сакко и Ванцетти были казнены за убийство"» и «„Альфред Смит проиграл президентские выборы в 1928 году" имплицирует „углы у основания равнобедренного треугольника равны"».

Однако парадокс исчезнет, если читатель отбросит предубеждение, связанное с обыденным пониманием слова «импликация», и обратит внимание на то, что, согласно своему определению, в исчислении суждений оно обозначает нечто иное. Это различие проявляется в обозначении первого вида импликации термином «формальная», а второго – «материальная» [43] . (Иногда первая называется «следованием», «тавтологической импликацией» или «строгой импликацией».) Утверждение формальной импликации, как мы видели в первой главе, не подразумевает допущения фактической истинности или ложности двух суждений, а обозначает лишь то, что они связаны благодаря собственной структуре (которую они разделяют со всеми другими суждениями такой же формы) и что невозможно, чтобы имплицирующее суждение было истинным, а имплицируемое – ложным. Имя «материальная импликация» мы придаем тому факту, когда первое из двух суждений ложно или когда второе истинно. При этом указанные два вида импликации не являются несвязанными друг с другом. Формальная импликация силлогизма означает, что в любом частном выражении силлогизма присутствует материальная импликация между посылками и заключением. Однако данное рассмотрение не учитывает того факта, что в каждом силлогизме имеет место необходимость, основанная на элементе тождества, напрямую не присутствующем во всех других случаях употребления материальной импликации. Когда мы говорим: «Киты являются млекопитающими, и все млекопитающие обладают легкими, следовательно, киты обладают легкими», то здесь присутствует связь, которой нет в таком примере, как «„Данте родился в 1250 году" имплицирует „литий является металлом"», где истинность общего суждения обеспечивается за счет ложности первого и истинности второго. Однако здесь мы уже сталкиваемся с метафизическим вопросом о том, связаны ли все истины необходимым образом с конечной природой вещей.

Данный текст является ознакомительным фрагментом.