II. ИСЧИСЛЕНИЕ БЕСКОНЕЧНО–МАЛЫХ И ЕГО ОСНОВНЫЕ КАТЕГОРИИ

We use cookies. Read the Privacy and Cookie Policy

II. ИСЧИСЛЕНИЕ БЕСКОНЕЧНО–МАЛЫХ И ЕГО ОСНОВНЫЕ КАТЕГОРИИ

1. Бытие, небытие, становление. Приступая к логическому анализу всех основных категорий, оперирование с которыми создает науку математического анализа, мы должны помнить, что далеко не все, понятное математически, тем самым является понятным и с философской точки зрения. Часто бывает так, что математик ограничивается каким–нибудь очень коротким разъяснением или формулой, философ же затрачивает массу времени и пространства, чтобы эту короткую и простую формулу разъяснить для себя и понять. Точно так же нередки и случаи, когда весьма пространные математические выкладки для философа не имеют почти никакой цены и из массы доказательств важной оказывается только какая–нибудь одна идея. Тем не менее давно уже настало время, когда математический анализ требуется понять широко философски и ощущается насущная потребность вывести его из формалистического тупика и пустой, бессодержательной трактовки.

Мы рассмотрим ряд категорий, приводящих к самому понятию бесконечно–малого, потому что понятие это с логической точки зрения довольно сложное и те определения, которые мы имеем в руководствах по анализу, для нас слишком формалистичны и техничны. Они совсем не вскрывают ту логическую структуру, которая кроется в понятии бесконечно–малого.

Мы начнем с тех трех категорий, с той общезначимой диалектической триады, без которой невозможно вообще никакое логическое построение, и каждое логическое построение есть только вид этой триады, один из бесконечно разнообразных ее случаев. Это та триада, с которой начинается всякая диалектика:

1) бытие,

2) небытие (инобытие),

3) становление.

Тут прежде всего — бытие. Почему диалектика начинается с бытия? Потому что всё, всякая категория, прежде чем быть самой собой, должна просто быть. Прежде чем быть чем–нибудь и как–нибудь, надо сначала просто быть. Вот почему диалектика, желающая дать всю область знания в системе, необходимым образом начинает с «бытия». Бытие—первый шаг, первый жест, первое движение, первая точка диалектики. Без этой точки, без этого первоисточника никакое построение невозможно.

Далее, бытие не может остаться только бытием, просто бытием. Бытие не есть бытие вообще. Если бы оно всегда оставалось бытием вообще, мы никогда не смогли бы получить никаких конкретных форм бытия. Существует не просто бытие, но и разные виды бытия. А для этого нужна такая универсальная категория, которая бы сделала возможным существование этих разных видов бытия. Такой категорией является инобытие, т. е. иное, другое бытие, являющееся по отношению к первому общему бытию отрицанием его, отсутствием его, небытием. Как только мы положим бытие, так тут же необходимо полагать и небытие; это понятия соотносительные. Если есть черный цвет, то он может быть только тогда, когда есть (или по крайней мере мыслится) не–черный цвет. Если мыслится белое, значит, как–нибудь и где–нибудь существует «не–белое». Также и «бытие», если оно реально есть или мыслится, то тем самым есть или мыслится «инобытие».

Но стоит только немного задуматься над той антитезой бытия и небытия, как становится совершенно ясно, что остаться при такой антитезе совершенно невозможно. Если оставить эти две области бытия и небытия в их голой и абсолютной противоположности, то совсем не будет достигнута цель, ради которой мы и ввели понятие инобытия. Мы ввели его для того, чтобы вместо абстрактного и общего бытия получить его конкретные виды. Но если инобытие будет абсолютно оторвано от бытия и не будет как–то с ним совмещено, — не возникнет и никаких конкретных видов бытия. Необходимо их как–то объединить, эти категории бытия и небытия, как–то нащупать то, что есть в них общего и что могло бы нейтра–лизировать этот дуализм двух противоположных логических стихий. Но что значит найти общее, что значит объединить? Это значит найти такую новую категорию, где обе полученные уже содержались бы и где они были бы покрыты чем–то третьим, что их и объединило бы.

Такой категорией является становление. В становлении мы находим прежде всего то, что становится. Стало быть, тут бытие налично. Но вместе с тем здесь же мы имеем тоже и некое как бы отталкивание от этого бытия. Становление есть ведь некий процесс, где бытие все время меняется и переходит в другое. В каждый мельчайший момент своего становления бытие—все иное, иное и иное. Оно тут никогда не одно и то же. В каждый мельчайший новый момент бытие оказывается небытием в отношении к прежнему бытию, к бытию в его прежней форме. И таким образом, в каждый мельчайший момент становления становление оказывается и бытием, и небытием. Потому в диалектике и говорят, что бытие и небытие синтезируются в становление.

2. Целое, дробное, бесконечность. Тут мы пока еще у преддверия анализа бесконечно–малых, но пока еще не вошли в него, не получили еще самого понятия бесконечно–малого. Попробуем конкретизировать достигнутую нами диалектическую ступень — с тем чтобы дойти постепенно и до этого понятия.

Первое, с чем мы тут встретимся, — это понятие и область числа. Когда мы выставляли указанную диалектическую триаду, мы не имели в виду чисел, а говорили в применении вообще ко всяким возможным предметам мысли. Теперь необходимо эту же самую триаду провести в чисто числовой области.

Разумеется, различных форм приложения этой триады к области чисел очень много. Так, напр., если мы возьмем положительное число, то антитезой к нему будет, очевидно, отрицательное число, а синтезом, в котором соединится то и другое, будет, очевидно, нуль. Но эта триада неинтересна в смысле получения понятия бесконечно–малого, и она ничего не разъясняет нам в математическом анализе. Потому подробно говорить о таких построениях надо только в общей философии числа, но не в логике математического анализа. Что же в числе есть такого, диалектическое понимание чего приводит нас вплотную к математическому анализу?

Математический анализ есть исчисление бесконечно–малых. Стало быть, здесь мы находимся в области учения о бесконечном. Спрашивается: что такое бесконечность?

Самое простое и самое «понятное» популярному сознанию — это то, что бесконечность есть нечто, не имеющее конца. Хотя это как будто и ближе всего передает смысл данного понятия, тем не менее считать это вполне ясным совершенно невозможно. Как понимать это отсутствие конца? Обычно это понимается так, что, сколько бы мы ни двигались к границе, мы никогда не можем ее достигнуть. Другими словами, в понятие бесконечности вносят идею процесса. И это вполне справедливо, хотя, быть может, и недостаточно. Самое простое и самое понятное—это понимать бесконечность как бесконечный процесс. Однако этим нисколько задача не решается. Вместо того чтобы определить понятие, выраженное при помощи существительного («бесконечность»), мы в данном случае приходим к необходимости определять понятие, выраженное через прилагательное («бесконечный процесс»). И если мы там не понимаем, что такое бесконечность, то не станет она понятнее и здесь. Какой же процесс мы должны считать бесконечным? Вот вопрос, который теперь предстоит нам решить.

Пусть мы от 1 перешли к 2, от 2 к 3, от 3 к 4 и т. д. Спрашивается: можем ли мы когда–нибудь на этом пути получить бесконечно–большое число? Пусть мы знаем, что такое 2; и пусть нам известно, что такое 10. Можем ли мы путем прибавления отдельных единиц получить из двойки десятку? Конечно, можем. На пути прибавления к двойке отдельных единиц и лежит то самое число, которое называется десяткой. Но можем ли мы на этом же самом пути получить бесконечность? Очевидно, нет. Зная только одни конечные числа, мы, какими бы арифметическими операциями ни пользовались, никогда и никак не можем получить бесконечную величину. Это значит, что бесконечность отличается от конечных величин отнюдь не количественно, а качественно. Это какое–то особое качество среди количественных операций; и к нему нельзя прийти путем обычных количественных операций, но только путем «скачка».

Итак, ни голая процессуальность не определяет бесконечности, хотя и как–то входит в нее, ни голая количественность не определяет бесконечности, хотя тоже как–то входит в нее. Приходится, следовательно, искать иных путей для нахождения понятия бесконечности.

Обратим внимание на следующее. Бесконечность не увеличивается и не уменьшается от количественного ее увеличения и уменьшения. Стало быть, в каждом отдельном пункте бесконечность есть уже вся бесконечность, какие бы операции мы над ней ни производили. Каждый момент бесконечности есть и вся целая бесконечность. Раз оо + А (любое число) =оо, то ясно, что в бесконечности каждая отдельная ее часть равняется всей бесконечности, взятой в целом. Этого, разумеется, никогда не бывает в конечной области. Тут всегда часть меньше целого и целое больше части. Этим область бесконечности коренным образом отличается от области конечных величин. Тут, однако, кроется и еще одна категория. Простое тождество целого и части еще ничего не говорит о бесконечности, если эти категории брать самостоятельно. Нужно точнее определить способ отождествления целого и части и ясно ощущать форму этого отождествления. Этот способ и эта форма не могут быть статическими. Бесконечность, видели мы, есть прежде всего процесс. Следовательно, отождествление целого и части должно быть дано в процессе, в становлении. Становление должно объединить целое и часть или, вообще говоря, целое и дробное, и тут–то и необходимо искать категорию бесконечности.

Как же протекает этот процесс отождествления целого и части в бесконечности?

Чтобы перейти от целого к дробному, надо перейти от бытия к небытию. Дробное—инобытие целого. Целое, воплотившись в инобытие, превращается в отдельные части и их сумму. В целом все элементы существенно связаны один с другим, почему они и являются элементами, или частями. Когда же целое воплощено в инобытии, все его элементы тоже воплощены в инобытии, но они уже дискретны друг в отношении друга, так как всякое инобытие есть всегда прежде всего внеположность и саморазличение, самоотрицание. Итак, целое выражается внешне–инобытийным образом в дробном, в отдельных частях, в сумме частей, в том, что в отличие от внутреннего центра целости можно назвать всем. Всё — воплощенное в инобытии целое.

Но если так, то спрашивается: может ли инобытийная стихия выявить внутреннюю целость вполне и адекватно? Конечно, может. Тогда в инобытии мы находим именно всё. Но она может выявлять его и не полностью, не адекватно. Становление есть как раз такая категория, которая мешает в данном случае адекватному выявлению целости. В целом все дано сразу, а становление все дает постепенно, не сразу. Следовательно, если дать свободу стихии становления, то целое, хотя и будет все время дробиться на части (в инобытии) и будет в них постоянно присутствовать, оно никогда не получит полного выявления и всегда будет только стремиться к полноте выявления. Целое дробится на части, и эти части призваны выразить его целиком; но так как части эти тождественны с целым, то количество элементов целого присутствует в части, она тоже делится на те же части, а часть этой части опять, в силу своего тождества с целым, содержит в себе то же количество частей и т. д. и т. д. Идя по этому пути, мы никогда не сможем выразить всего целого при помощи его частей — и это потому, что части возникают в результате постепенного дробления, т. е. в результате становящегося дробления, в результате становящегося отождествления целого и частей.

Теперь мы можем дать некоторого рода логическую формулу, определяющую понятие бесконечности.

Бесконечность есть становящееся тождество (или становящийся синтез) целого и дробного.

Это простейшая концепция бесконечности, без которой невозможно будет понять и отдельных видов бесконечности. Тут мы видим, что без момента целости нельзя получить понятие бесконечного. Видим также, что в бесконечность входит и момент процесса, становления. Необходимо полнейшим образом представлять себе участие каждого из этих моментов в общем понятии бесконечности.

Целое дробится, выражается своими частями. По условию целое должно содержаться в своей части — тем самым возникает их тождество. Но части должны мыслиться не стационарно, но в последовательном возникновении, в становлении. Тогда получается невозможность исчерпать все части целого, т. е. образуется бесконечность.

В бесконечности дана целость, но не сама по себе, а как подчиненный момент. Если бы ее тут не было, то не могло бы быть и дробления, т. е. не было бы никакого перехода к мельчайшим частям и не было бы, значит, ухода в бесконечность. В бесконечности дана дробность, но опять–таки не сама по себе, а как подчиненный момент. Если бы ее тут не было — опять не могло бы возникнуть процесса дробления и не могло бы возникнуть ухода в бесконечность. Бесконечность не целое и не дробное. Но она и целое, и дробное, и нечто гораздо большее, в чем обе эти категории как бы взаимно растворяются. Это целое, из объединившее, есть становление одного другим, становление целого дробным и дробного, частного—целым. В бесконечности все последовательные моменты равны один другому, но они в то же время и различны, так как возникают они в процессе становления. Целое стремится выразиться в убывающих частях и не может, и части стремятся стать целым и не могут. Все это в процессе становления по самой природе своей алогично, т. е. нерасчленимо, неразличимо.

Бесконечность, таким образом, есть вид становления. От становления рообще этот вид становления отличается тем, что тут совпадает не просто бытие с небытием, но именно целое с дробным. Каждый момент бесконечности представляет собою не просто переход от бытия к небытию и от небытия к бытию, т. е. не просто уничтожение и возникновение, но переход к раздробленности и обратно, т. е. рост целостности и дробления. Когда мы движемся в области бесконечности от одной точки к другой, то тем самым мы, во–первых, удаляемся все в большую дробность, но в то же время, во–вторых, обнимая все большее и большее количество точек, мы неизменно стремимся ко все большей и большей цельности. Такая структура числа, где эти два процесса являются существенно тождественными, такая структура числа и называется бесконечностью.

Из предыдущего вполне ясно, что бесконечность меньше всего определяется размерами. Бесконечность помещается в любых конечных размерах. Если мы возьмем линию длиною в 5 см, то на ее протяжении поместится бесконечное количество точек. Если мы возьмем линию длиною в 1 см, то, очевидно, на ней тоже поместится бесконечное количество точек. Если мы возьмем линию в 0,1 см, в 0,01 см, в 0,001 см длиною и т. д. и т. д., то и на этих линиях, как бы малы или велики они ни были, тоже помещается бесконечное количество точек. Отсюда совершенно ясно: бесконечная величина определяется не абсолютными размерами числа или вещи, но определенно— взаимоотношением их целости и их дробности, а именно тем взаимоотношением, когда они даны как полное тождество.

3. Антиномии и типы бесконечности. Вопрос об антиномиях, равно как и вопрос о типах бесконечности, — не только сложная вещь, но она потребовала бы и слишком пространного изложения. Заниматься этим, однако, должны теоретико–философские сочинения, в то время как настоящее сочинение имеет очень узкие цели, да и занимается математический анализ, если его брать в чистом виде, только одним специфическим типом бесконечности. Поэтому, не развивая антиномики бесконечного в систематическом виде, формулируем то, что уже было сказано выше, в расчлененно–антиноми–ко–синтетической форме и тем самым дадим по возможности четкое изображение диалектики понятия бесконечности.

I. 1. Целое состоит из частей, так как в нем ничего и нет, кроме частей.

Это значит, что целое тождественно со своими частями.

Но тогда оно распростерто по всем своим частям и, след., находится везде.

Итак, целое, состоя из частей, находится везде.

2. Целое не состоит из частей, так как ни одна часть, взятая сама по себе, не говорит о целом, и, след., не говорят о нем и все части, взятые вместе.

Это значит, что целое не содержится в своих частях, т. е. оно не находится нигде.

Итак, целое, не состоя из частей, нигде не находится.

3. Целое и состоит, и не состоит из своих частей, т. е. оно сразу и одновременно и находится везде, и не находится нигде.

Но «состоять» и «не состоять», равно как и «везде» и «нигде», связаны между собой антитетически, т. е. как бытие и небытие. Поэтому связаны они между собой как становление одного другим.

Следовательно, целое и его части находятся в процессе становления, в котором они взаимно переходят одно в другое, т. е. целое неразличимо становится самими частями и части неразличимо становятся целым.

II. 1. Целое—везде.

Это значит, что части его взаимно неразличимы.

2. Целое — нигде.

Это значит, что части его взаимно различимы.

3. Целое—и везде, и нигде.

Следовательно, части целого находятся в процессе становления, в котором они взаимно переходят одна в другую, т. е. каждая отдельная часть неразличимо становится каждою другою частью.

III. 1. Целое становится частями, как и части целым; и части становятся одна другою.

2. Но в становлении отождествлены бытие и небытие.

Здесь бытие становится небытием; стало быть, оно уничтожается.

И небытие становится бытием; стало быть, оно возникает.

Становление, следовательно, есть противоречие возникновения и уничтожения.

Разрешается это противоречие в такой категории, где возникновение и уничтожение совпадают.

Эта категория есть то, что получается в результате становления, т. е. ставшее. И ставшее возникает в каждый мельчайший момент становления; поэтому ставшее в свою очередь пребывает в процессе становления, рассыпаясь на бесконечное количество ставших моментов и из них восстановляясь.

3. Целое и части, а также части между собой возникают одно из другого и уничтожаются одно в другом при полном отождествлении этих процессов. Становящееся тождество возникновения и уничтожения есть бесконечность.

В результате этого бесконечностью нужно считать такой процесс, в котором каждый мельчайший новый момент есть возникновение нового, небывалого и в то же время уничтожение как всех старых моментов, так и самого себя.

Полученное нами здесь понятие бесконечности может быть развито в трех разных направлениях.

Во–первых, можно в этом понятии выдвигать на первый план момент количества, счетности. Хотя, строго говоря, бесконечность не есть нечто количественное и ее нельзя получить в результате счета, все же она относится к числовой сфере, и какую–то количественность она в себе содержит. Эта количественность совсем особого рода. Тут отдельные моменты количества слиты один с другим до полной неразличимости. И тем не менее они все же наличны. Упирая на счетность, мы получим тип бесконечности, который есть.

I. Арифметическая бесконечность. С этим типом бесконечности мы стараемся производить обычные арифметические операции, хотя своеобразие этой категории приводит к своеобразию и операций над нею.

Во–вторых, в общем понятии бесконечности мы можем выдвинуть то, что является антитезисом всякой раздельной счетности, т. е. чистую стихию становления, чистую процессуальность, становящуюся неразличимость. Без этого момента бесконечность также немыслима, хотя она и не есть только этот момент. Этот тип бесконечности и есть тот тип, который рассматривается в чистом математическом анализе. Отсюда ее можно назвать и соответствующе:

II. Аналитическая бесконечность.

Наконец, можно выдвигать в общем понятии бесконечности оба этих момента вместе — раздельную счетность и неразличимое становление (невозможность счета). Тогда первый момент воплотится на втором, как всякая отвлеченная идея воплощается на безразличном материале. Идея — раздельность, логическая последовательность, форма и система; становление безраздельно, алогично и бесформенно. Объединение их дает фигурную бесконечность, определенным образом оформленную, «упорядоченную», ту, которая является предметом особой математической науки, — учения о множествах. Ей можно дать тоже свое название.

III. Аритмологическая бесконечность.

Арифметическая, аналитическая и аритмологическая бесконечности суть три наиболее ярко отличающиеся друг от друга типа бесконечности. Немудрено, что ими занимаются три столь различные математические науки.

Нас в дальнейшем будет интересовать, конечно, только второй тип бесконечности — аналитический.

4. Непрерывность (постоянная и переменная величина), прерывность и предел. Однако прежде чем войти в рассмотрение самого математического анализа, необходимо определить еще ряд категорий, которые так же основоположены для анализа, как и понятие бесконечности. Их тоже обычно излагают в случайной форме, не связывая в диалектическую систему, в то время как это касается самых основных сторон математики, и они не могут не иметь диалектического строения, если все вообще категории возникают диалектически.

Ряд категорий, которые требуют нашего рассмотрения, отличаются одним общим признаком. Число есть непосредственное бытие; в нем нет еще различия между самим числом и его значением. До сих пор мы имели число само по себе. Целое, дробное и бесконечное число есть значения числа в смысле его внутреннего строения. Чтобы узнать, является ли данное число целым или дробным, необходимо всмотреться в само число непосредственно, не обращая никакого специального внимания на фон, его окружающий. Это касается и не только числа. Чтобы судить, является ли данная вещь цельной, надо, очевидно, рассмотреть строение самой вещи, как оно дано в контурах, внутри контуров данной вещи. Когда сосуд, напр., имеет трещину или дыру, то для констатирования этого достаточно только изучить сосуд в тех границах, которые даны очертанием этого сосуда. И мы вполне будем в состоянии определить, является ли данная ваза целой, или она разбита. Однако о значении числа или вещи можно говорить и с точки зрения их внешней судьбы. Можно представить себе, что вещь мыслится совершенно неизменной сама по себе, но что она погружена или вовлечена в какое–нибудь изменение, оставаясь сама по себе целой. Можно иметь одно и то же число или комбинацию чисел и, оставляя их в одном и том же виде, придавать им те или иные внешние значения. Тут не будет ни просто числа, взятого в его непосредственности, вне каких бы то ни было количественных значений, ни числа, в котором имеются в виду только изменения во внутренней структуре. Тут число вступит в новые значения при полном сохранении внутренних структур или, вернее, независимо ни от каких внутренних структур.

Прежде всего величина с этой внешней точки зрения может никак не меняться; она может иметь, так сказать, нуль изменения. Такую величину называют постоянной величиной. Антитезой к этой постоянной величине является, очевидно, переменная величина.

Что такое постоянная величина и что такое переменная величина, это известно уже из элементарной математики. В анализе эта пара понятий играет, однако, гораздо большую роль. Возьмем, напр., площадь треугольника. Из элементарной геометрии известно, что эта площадь равняется половине произведения основания на высоту. Эта формула — «половина произведения основания на высоту» — нисколько не зависит от величины самого основания и самой высоты. Самая эта связь основания и высоты для выражения площади вполне постоянна. Еще ярче, однако, антитеза постоянной и переменной величин в случае, когда выставляется теорема: «сумма углов треугольника равняется двум прямым». Сколько бы ни увеличивать и ни уменьшать отдельные углы треугольника, сумма их все равно остается равной двум прямым. Ясно, что величины отдельных углов треугольника суть переменные величины и сумма всех трех сторон треугольника есть величина постоянная. В физике устанавливается закон о том, что произведение давления газа на его объем есть величина постоянная. Следовательно, если меняется давление, то соответствующе меняется объем газа, произведение же обеих величин никогда не меняется. Ясно, что объемы и давления суть в этом законе переменные величины, их же произведение—постоянная величина.

Вдумываясь в существо этих двух категорий, мы отчетливо видим, что отличие их от величины просто, от величины вообще заключается в том, что тут «величина вообще» содержит в себе еще особый слой, слой внешней характеристики. Постоянная и переменная величина есть, прежде всего, величина просто, а во–вторых, еще утверждается, что эта величина имеет такое–то или такое–то значение. Это значение — чисто внешне в отношении величины, взятой самой по себе. В одном случае угол треугольника равен 30°, другой раз—45°, третий раз — 60° и т. д. и т. д. Эта величина может быть какой угодно (имея в виду общую сумму углов, равную двум прямым). Размеры угла, ясно по самому смыслу, не имеют никакой связи с самим понятием угла. Поэтому размерность есть нечто внешнее в отношении самого понятия угла. И на этом основании мы и говорили, что постоянная и переменная величины есть внешнее инобытие числа и эта внешность, конечно, к тому же вполне отождествлена с непосредственно данным числом, с числом самим по себе.

Но интереснее всего то, что получается от соединения этих двух категорий—постоянной и переменной величин. Диалектический синтез всегда особенно интересен; он часто таит в себе полную неожиданность. Так, из синтезирования целого и дробного получалась (быть может, с первого взгляда довольно неожиданно) категория бесконечности. Что же получится из синтезирования постоянной и переменной величин? Какова та категория, в которой обе эти категории совпадают совершенно, точно сливаясь в полную неразличимость на фоне вполне новой и в них не содержащейся конструкции?

Такой категорией является непрерывность.

Подобно тому как бытие и небытие объединяются в становление, так и постоянная величина с переменной объединяются в непрерывной величине. Непрерывная величина, во–первых, есть нечто постоянное. В самом деле, самый смысл непрерывности заключается в том, что каждый ее момент совершенно одинаков со всяким предыдущим моментом. Непрерывная величина потому и «не прерывается», что она везде одинаковая, что она не меняется, что она всецело постоянная. Таким образом, постоянство, несомненно, входит в категорию непрерывности в качестве конститутивного момента; непрерывность без него немыслима. Однако также ясно, во–вторых, что непрерывность требует для себя и момента изменения. Это значило бы, что вся непрерывность свернулась бы в одну точку. Допустим, что в непрерывности нет изменения. В то же время, однако, в непрерывности мыслится некий процесс. Непрерывность есть именно процесс, т. е. движение, изменение; но это такой процесс, в котором все моменты процесса сливаются в одно и то же, в один и тот же момент. Если различать в каждом моменте самый факт этого момента, субстанцию, и, с другой стороны, его смысловую, идейную сторону, то необходимо сказать, что по факту, по субстанции, все эти точки абсолютно разделены, внеположены, находятся одна вне другой; с точки же зрения смысла, идеи все они суть нечто одно, совершенно одно, неразличимое тождество и единство. В этом и заключается тайна непрерывности: в ней дано фактическое движение[225], движение по факту, т. е. разнообразие, бесконечное фактическое разнообразие отдельных точек; и с другой стороны, тут дано полное смысловое идейное отождествление всех бесконечных точек, как бы они ни возникали и сколько бы их ни возникало.

Непрерывная величина есть тождество постоянной и переменной величин.

Непрерывность, однако, не может быть утверждаема сама по себе, без другой категории, которая с нею соотносительна. Раз мыслится непрерывность, то тем самым должна мыслиться и прерывность. Одно без другого совершенно немыслимо. Таким образом, достигнутый нами синтез непрерывности в свою очередь переходит в новый антитезис, в прерывную величину, и, следовательно, в свою очередь требует еще нового синтеза.

Синтезом прерывности и непрерывности является предел.

Предел немыслим вне понятия процесса. Предел есть то, что достигается в течение того или иного определенного процесса. Какой это процесс? Если это есть именно процесс достижения, то это достижение происходит постоянно, постепенно. Чем больше и дальше двигаемся мы в сфере этого процесса, тем ближе мы к пределу, тем больше мы его достигаем. Итак, предел есть некое движение, изменение и некий процесс.

Спросим теперь себя: какой же именно это процесс? С одной стороны, даже самое понятие предела говорит о некоей определенности и конечности. Движение происходит в определенном направлении, и оно имеет какую–нибудь определенную, конечную цель. Без этой идеи не может существовать никакого предела. Однако, с другой стороны, предел в математике не мыслится просто, как граница и конец. Этот предел в математике всегда мыслится как нечто недостижимое, хотя и конечное, как нечто притягивающее к себе издали приближенную величину, но никогда не совпадающее с этой приближенной величиной. Предел, с одной стороны, конечен, а с другой—эта его конечность никогда не может быть вполне адекватно охвачена. Как это можно совместить?

Совместить это можно только тем обычным диалектическим путем, который от бытия и небытия ведет к становлению. Необходимо, чтобы достижение конечного предела и постоянное его недостижение совместились во взаимном становлении, т. е. так, чтобы достигнутая конечность все время сдвигалась с места и заменялась другой, тоже достигнутой конечностью и чтобы бесконечное, постоянное достижение выражалось, тоже постоянно, в определенных конечных пунктах. В таком становлении мы получаем, следовательно, бесконечный ряд конечных величин, но эти конечные величины, уменьшаясь все больше и больше, приближаются к определенной величине, хотя никогда ее и не могут достигнуть. Становление, как мы видели, всегда алогично: оно неразличимо внутри себя и оно не имеет никаких точных границ и на своей периферии. В данном случае в процессе становления находится прерывность в отношении непрерывности и непрерывность в отношении прерывности. Это значит, что прерывность должна становиться непрерывностью, а непрерывность должна становиться прерывностью. Поскольку становление есть всегда постепенный процесс, постольку прерывность становится непрерывностью постепенно, сплошно, последовательно, равно как и непрерывность — прерывностью. Возможно это только так, что прерывность делается все меньше и меньше прерывистого, т. е. промежутки между прерывными моментами делаются все меньше и меньше и таким образом прерывность все больше и больше превращается в непрерывность. Точно так же и непрерывность по мере своего продвижения все больше и больше покрывается прерывными точками, и эти прерывные точки застилают ее все гуще и гуще — правда, без всякой возможности когда–нибудь достигнуть абсолютного перекрытия непрерывности прерывностью. Заметим, что становление алогично не только в том смысле, что оно неразличимо само в себе, само внутри себя, но и в том, что оно неразличимо и по своей периферии, т. е. не имеет никаких законченных границ и в этом смысле безгранично. Отсюда понятно, почему становление прерывности непрерывностью или непрерывности прерывностью никогда не может быть кончено; по самому смыслу своему оно абсолютно беспрерывно. И значит, предел, диалектически синтезирующий непрерывность и прерывность — по типу категории становления, — есть в одно и то же время и полная недостижимость для числового процесса, и выраженность, достигнутость в каждый отдельный момент этого процесса, причем эта выраженность и достигнутость бесконечно интенсифицируется, возрастает.

Предел—это та категория, которая (правда, в довольно вялом виде) применяется уже и в элементарной математике. Главное ее место, однако, в математическом анализе; и тут на ней, можно сказать, построена целая наука.

Пусть в круг вписан квадрат. Если мы удвоим количество его сторон, то площадь его, конечно, увеличится и периметр его тоже увеличится. Это удвоенное количество сторон может быть удвоено еще раз, еще раз и еще раз. Оно может быть удвоено до бесконечности. Периметр, последовательно меняющий свою форму в зависимости от количества удвоений, будет стремиться, очевидно, к окружности и в пределе совпадет с нею. Окружность, говорят, есть предел вписанных многоугольников при бесконечном увеличении количества сторон, равно как и предел описанных многоугольников при бесконечном увеличении количества сторон.

Здесь окружность есть нечто определенное и конечное; каждый многоугольник, вписанный или описанный, с любым количеством сторон, есть тоже величина определенная и конечная; но многоугольник тут дан не сам по себе, но в своем становлении (в смысле увеличения количества сторон); потому и количество сторон все время растет, по длине они делаются все меньше, и, значит, в целом же они приближаются все больше и больше к окружности; окружность для них—предел. Тут вполне отчетливо выступают две основные категории—непрерывности и прерывности и их синтетическое взаимопревращение, сплошной и бесконечный переход непрерывности в прерывность и прерывности в непрерывность.

Итак, вот диалектическая схема указываемых нами понятий: непрерывность, прерывность, предел, при этом непрерывность сама возникает как синтез постоянной и переменной величин.

5. Бесконечно–малое и бесконечно–большое. Только теперь мы можем формулировать то основное понятие, на котором строится весь математический анализ, — понятие бесконечно–малого (и, значит, бесконечно–большого). Оно возникает как напряженное, конденсированное выражение всех только что рассмотренных нами категорий.

Непрерывность (с постоянной и переменной величинами), прерывность и предел — все это, вместе взятое, может рассматриваться как нечто целое. Именно — это то, что противостоит числу, взятому в его чисто арифметическом виде, т. е. числу, взятому как непосредственное бытие. Когда мы берем числа натурального ряда и производим над ними арифметические действия, то здесь не возникает никаких сопоставлений каждого отдельного числа с тем или иным его внутренним или внешним функционированием. Произведя, напр., деление одного числа на другое, мы не ставим никаких вопросов о том, являются ли эти числа, делимое, делитель и частное, величинами постоянными, переменными, прерывными, непрерывными или предельными. Никаких таких вопросов тут совершенно не возникает. Это понятно. Все эти вопросы связаны с числом в том или ином опосредствованном виде. Когда мы говорим «5», «10», « 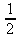», «3» и т. д., мы производим арифметические операции над числами в том их виде, как они и даны. Когда же мы говорим, напр., «переменная величина», то тут имеется в виду не только непосредственная значимость числа самого по себе, но еще и его определенное логическое отношение к тому фону, на котором оно дано. Тут—опосредствованная значимость числа.

Но если это так, то число арифметическое, как непосредственно значащее, число в смысле непрерывности, прерывности и предела, как опосредствованно значащее, находятся друг в отношении друга в состоянии диалектической антитезы. Если по общей диалектической схеме непосредственность признать за бытие, то опосредст–вованность необходимо будет признать за небытие, и между обеими категориями возникает диалектическое противоречие. Оно ждет разрешения и синтеза.

Что нужно для синтеза? Нужно, чтобы непосредственно значащее арифметическое число восприяло на себя категории непрерывности, прерывности и предела, т. е. чтобы оно лишилось своей стационарной значимости и проб [уд ]ило в себе эту двуплановость, требуемую данными категориями. С другой стороны, также необходимо, чтобы эти три категории воплотились на реально значащем числе, или величине, и перестали быть только отвлеченными признаками неизвестно каких величин. Этот диалектический синтез и совершается в понятии бесконечно–малого.

Самое простое математическое определение бесконечно–малого есть следующее. Бесконечно–малое есть переменная величина, имеющая своим пределом нуль. С виду простое, это определение, однако, содержит в себе немало разных подчиненных моментов, и они враздробь указаны нами в предшествующем, подготовительном изложении.

Во–первых, бесконечно–малое есть величина переменная. Одно уже это тянет за собою всю систему категорий, которую мы наметили выше. И уже один этот момент накладывает неизгладимую печать на всю изучаемую нами категорию. Бесконечно–малое—это сплошь стихия становления, изменения; тут ничто не стоит на месте, все движется и беспокойно требует расширения, углубления, распространения.

Во–вторых, бесконечно–малое есть такая переменная величина, которая имеет определенный предел. Отнюдь не всякая переменная величина имеет предел, стремится к пределу. Возьмем самую обыкновенную синусоиду. Эта равномерно вьющаяся вокруг прямой кривая никуда не стремится, ни к какому пределу не стремится, сколько бы ее ни продолжали. Она проходит одни и те же значения бесконечное число раз; эти значения неизменно повторяются, и кривая от этого ровно ни к чему не приближается и не стремится ни к какому пределу. Бесконечно–малое [же] как раз имеет такой предел, неизменно стремится к нему; предел управляет бесконечно–малым и притягивает его к себе из таинственного полумрака бесконечности. Это создает для понятия бесконечно–малого вполне оригинальный стиль, который еще усиливается от других элементов этого понятия. Подчеркнем, что изменение, поскольку речь зашла о пределе, дано тут не само по себе, но в становлении, в алогическом становлении. Оно само стремится в какую–то даль, и стремится сплошно, неразличимо, безраздельно. Предел, следовательно, достигается тут при помощи бесконечного процесса приближения. Другими словами, этот предел никогда и нигде не достигается, а дано только вечное стремление, вечное движение, неустанный уход в бесконечные дали.

В–третьих, бесконечно–малое есть такая переменная величина, которая имеет своим пределом нуль. Нуль в качестве предела рисует всю нашу картину вечного стремления совсем в другом, в небывалом виде. Что это значит? Что значит это вечное стремление—и к чему же? К нулю, в ничто, в небытие! Это значит, что дух, живущий по законам бесконечно–малого, не только стремится куда–то вдаль и не только это стремление вечно, но, кроме того, тут ставится задача исчерпания бытия, охвата бытия до последней его точки, использование его до тех пор, пока не останется в нем нуль бытия, пока не перестанет существовать само бытие и не превратится оно в ничто. Инфинитезимальный дух хочет исчерпать все бытие, пережить всю стихию жизни, завоевать до последней точки все существующее, охватить его умом и сердцем, сделать соизмеримым с собою, адекватным себе, превратить его из сверхразумной бездны в ощутимую бездну, перевести ее всю–всю целиком на язык своего субъекта, своего сознания, потопить и растворить в глубинах собственной личности. Вот что значит это стремление бесконечно–малого к нулю как к своему пределу; и вот почему это не вообще переменная величина и не вообще процесс, хотя бы и бесконечный процесс, но процесс, имеющий своею целью нуль, исчерпание охватываемого им бытия до нуля.

В этом смысле бесконечно–большое мало чем отличается от бесконечно–малого. Если бесконечно–малое есть переменная величина, стремящаяся к нулю, то бесконечно–большое, очевидно, есть отношение единицы к этому бесконечно–малому. Если ?= 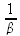, то при условии lim ? = 0, lim ?=?, а при условии lim ? =?, litn ? = 0. Чем больше уменьшается ?, тем больше увеличивается ?; и когда ? стремится к нулю, ? стремится к бесконечности. Наоборот, чем больше а, тем меньше ?; и когда ? стремится к бесконечности, ? стремится к нулю. Тут вполне ясна связь, существующая между бесконечно–малым и бесконечно–большим. Когда мы имеем какой–нибудь цельный предмет, то, уходя в его глубину с целью исчерпать его до нуля, пользуясь идеей бесконечного процесса, мы сразу получаем и бесконечно–малое, и бесконечно–большое: бесконечно–малое мы получаем, если имеем в виду отдельные моменты процесса, и бесконечно–большое, — если имеем в виду весь пройденный путь. Если сравнить все целое с отдельной стремящейся точкой, мы получаем уже не просто целое, но целое, разработанное именно с точки зрения этой отдельной стремящейся точки, с точки зрения этого бесконечно–малого, т. е. получаем бесконечно–большое. И наоборот, сравнивши бесконечно–большое, возникшее из всех бесконечно–малых, с целым, мы замечаем, что оно могло возникнуть действительно только из передвижения бесконечно–малого, т. е. получаем идею бесконечно–малого. Так связаны между собой эти оба понятия, являясь, в сущности, одной и той же идеей, рассматриваемой только с разных точек зрения.

Можно дать еще другое определение бесконечно–малого, хотя это определение, конечно, в сущности своей может быть только тождественным с первым. Именно, бесконечно–малое определяют еще так. Бесконечно–малое есть такая переменная величина, которая может стать меньше любой заданной величины. Пожалуй, это определение несколько ярче подчеркивает момент процессуальное, играющий такую огромную роль во всем понятии бесконечно–малого. Тут важны именно слова «может стать меньше любой заданной величины». В них выражена стихия становления, без которой бесконечно–малое не существует. В предыдущем определении момент становления и процессуальности выражен слабее, но зато лучше выражена идея исчерпания неисчерпания, идея, так сказать, «объятия необъятного». Этот момент тоже основной в учении о бесконечно–малом. И таким образом, оба определения, имея в виду один и тот же предмет, подчеркивают в нем одинаково важные, хотя и различные, стороны, причем каждая из этих сторон необходимо предполагает другую, так что в конце концов безразлично, какую сторону выдвигать и на каком определении останавливаться.

Итак, бесконечно–малое есть диалектический синтез числа в его непосредственном (арифметическом) бытии и числа в его опосредствованном (инобытийном в отношении к арифметическому) бытии. Бесконечно–малое есть прежде всего некая чистая величина, и в этом сказывается участие здесь арифметического элемента. С другой стороны, это не просто арифметическая величина со всей ее статической структурой, но такая величина, которая вобрала в себя и воплотила в себе эти понятия, инобытийные в сравнении с арифметической статической раздельностью, — непрерывность, прерывность, предел. Поэтому можно дать такую диалектическую формулу понятия бесконечно–малого.

Бесконечно–малое есть тождество (синтез) непосредственно–арифметической значимости числа и опосредствованно–инобытийно–го, внутренно–внешнего становления. Этот момент внутренно–внеш–него становления важен потому, что, как мы помним, бесконечность уже сама по себе, независимо от ее специального — инфинитези–мального, или аналитического, типа есть синтез целого и дробного, т. е. синтез внутренних особенностей строения числа, в то время как природа непрерывности, прерывности и предела возможна у нас на почве именно внешней ориентированности числа на окружающем его фоне.

Предложенная формула, конечно, совершенно тождественна с двумя указанными, чисто математическими определениями. Но это есть формула философская, логическая или, точнее, диалектическая, т. е. основанная на анализе и антиномико–синтетической структуре понятий, в то время как те два определения суть чисто математические определения, т. е. основанные на формально–числовом, формально–счислительном объединении счетных величин. В диалектике — понятия и категории, в математике — числа и величины. В диалектике—антиномико–синтетическая связь понятий и категорий, в математике—счислите л ьно–счетная связь чисел и величин.

6. Сущность функции. Есть, однако, еще категория, столь же глубоко определяющая стиль науки о бесконечно–малом, как и само понятие бесконечно–малого. Это понятие функции. Школьные математики и это понятие угробили до той степени, когда оно превращается в сухую и чисто вычислительную категорию, имеющую только внешне–прикладное значение. Это понятие гораздо богаче школьного его употребления, в особенности если иметь в виду его социально–исторические корни.

Что такое функция и когда это понятие играет наибольшую роль в математике и философии?