§ 3. Виды измерения дисперсии

§ 3. Виды измерения дисперсии

Мы видели, что группы могут отличаться друг от друга не только своими центральными тенденциями, но также и степенью разброса составляющих их значений.

Амплитуда вариации

Простой способ указать степень разброса значений в группе – это установить амплитуду вариации. Она представляет собой численную разность между максимальными и минимальными значениями признака в рассматриваемой группе. Если доходы в Соединенных Штатах варьируются от $500 до $10 ООО ООО, то амплитуда вариации будет равна $9 999 500. Однако этот метод не является удовлетворительным, поскольку, во-первых, крайние значения вариации могут быть неизвестны, а во-вторых, поскольку добавление или элиминация нескольких зарплат на краях совокупности могут существенно изменить амплитуду вариации. Более того, амплитуда вариации не говорит нам о том, как именно распределяются различные доходы внутри группы. Две группы чисел 1, 5, 5, 6, 6, 7, 7, 7, 10 и 1, 2, 2, 2, 2, 10 имеют одинаковую амплитуду вариации, хотя форма распределения в каждой из этих совокупностей является разной.

Среднее отклонение

Можно найти и более точные методы для обозначения степени вариации. Предположим, рост мужчин в определенной группе, измеренный в дюймах, таков: 61, 63, 64, 65, 65, 66, 67, 68, 69, 72. Средний рост равен 66 дюймам. Теперь высчитаем отклонение каждого роста от среднего роста путем вычитания последнего из каждого отдельного роста. (Можно взять любой средний показатель в качестве основы для высчитывания отклонений. Мы же для простоты ограничимся средним арифметическим.) Отклонения таковы: -5, -3, -2, -1, -1, 0, 1,

2, 3, 6. У нас может возникнуть желание высчитать среднее арифметическое этих чисел. Однако это бесполезно, поскольку сумма отклонений от среднего значения всегда равна нулю. Однако мы можем пренебречь отрицательными знаками в отклонениях и высчитать среднее арифметическое. Полученный результат будет называться средним отклонением, или средней ошибкой. Среднее отклонение в нашем случае равняется 24/10, или 2,4.

Среднее отклонение приписывает одинаковую значимость как большим, так и малым отклонениям. Вообще, чем меньше среднее отклонение, тем более сконцентрированы исследуемые предметы вокруг среднего значения. Все факторы, упоминавшиеся при обсуждении среднего арифметического, также релевантны и в случае со средним отклонением.

Однако нам следует обратить внимание на то, что большое среднее отклонение не является необходимым признаком большой флуктуации в значениях группы. Быть большим можно только относительно некоторого стандарта. Если мы многократно измерим высоту горы, то среднее арифметическое наших измерений может равняться 5000 футов, а среднее отклонение – 10 футам. По сравнению со средним арифметическим среднее отклонение является маленьким числом. Однако если бы мы измеряли длину квартала в городе, то среднее отклонение в 10 футов было бы существенным. По этой причине среднее отклонение иногда делится на средний показатель, относительно которого измеряются отклонения. Получившийся результат называется «коэффициент дисперсии». В предыдущем примере об измерении роста людей этот коэффициент равнялся 2,4/66, или 0,036+.

Стандартное отклонение

Для многих целей, особенно тех, в которых преобладают элементы теории вероятности, в качестве меры дисперсии рассматривается стандартное отклонение. Оно вычисляется путем деления суммы квадратов отклонений от среднего показателя на количество предметов в группе и извлечения из получившегося результата квадратного корня. В примере с измерением роста мы получаем

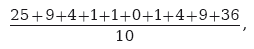
что равняется 9 и является средним арифметическим суммы квадратов отклонений. Стандартное отклонение равняется

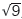, или 3. Если x1, х2, хn являются отклонениями от среднего арифметического из n значений, то ?х, т. е. стандартное отклонение, равно

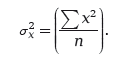
Стандартное отклонение, построенное указанным образом, демонстрирует экстремальные значения отклонений. При возведении отклонений в квадрат наибольшие из них обретают больший вес в общей сумме по сравнению с меньшими отклонениями. Относительно полезности стандартного отклонения нельзя сказать ничего до тех пор, пока не станут известными предположения, сделанные относительно группы значений, для которых оно высчитывается. Однако в целом стандартное отклонение является измерением дисперсии, которое в наименьшей степени подвержено влиянию флуктуаций в выборке по сравнению с другими измерениями. Если распределение в группе является примерно симметричным и если расстояние, равное стандартному отклонению, отграничено с каждой стороны среднего показателя, то около 2/3 всех предметов группы будут находиться внутри отграниченной области. В нашем примере с измерением роста эти отграничения выражаются записью: 66 ± 3. И действительно, около 2/3 величин находится между 63 и 69. Квартильное отклонение

Еще один способ измерения отклонения можно получить в результате расстановки предметов по мере их увеличения и отыскания тех трех значений (item), которые делят общую последовательность на четыре равные части. Эти значения называются «первый квартиль», «второй квартиль» (или медиана) и «третий квартиль». Если Q1 – это первый квартиль, a Q3 – третий, то квартильное отклонение определяется как (Q3 – Q1) / 2. Очевидно, что половина значений группы должна лежать между первым и третьим квартилями. По этой причине квартильное отклонение иногда также называется «вероятностной ошибкой». Если мы используем запись 65,5 ± 2 (где 65,5 является термином, находящимся посередине между первым и третьим квартилем, а 2 – квартальным отклонением), то внутри указанных границ (63,5 и 67,5) будет столько же значений, сколько и снаружи. Иными словами, предполагается, что когда мы произвольно выбираем какие-либо значения группы, то вероятность того, что мы выберем значение, находящееся внутри указанных границ, равна вероятности того, что мы выберем значение за их пределами. Однако выбор термина «вероятностная ошибка» здесь не вполне удачен и сбивает с толку, т. к. в литературе по данной теме этим термином принято обозначать и другие вещи.

Данный текст является ознакомительным фрагментом.