§ 2. Непосредственные дедуктивные умозаключения

§ 2. Непосредственные дедуктивные умозаключения

В непосредственных умозаключениях вывод осуществляется из одной посылки путем ее преобразований: превращения, обращения, противопоставления предикату и по «логическому квадрату».

Выводы в каждом из этих умозаключений получаются в соответствии с определенными логическими правилами, которые обусловлены количест­венной и качественной характеристиками исходного суждения.

Превращение - разновидность непосредственного умозаключения, в ко­тором изменяется качество посылки без изменения ее количества. Оно осу­ществляется двумя способами:

а) путем двойного отрицания, которое ставится перед связкой и перед предикатом:

S есть Р ? S не есть не-Р

Например, «Все адвокаты - юристы» ——>- «Ни один адвокат не явля­ется не юристом». Заключение здесь опирается на правило вывода: двойное отрицание равносильно утверждению;

б) путем перевода отрицания из предиката в связку:

S есть не-Р ? S не есть Р

Например, «Некоторые свидетельские показания недостоверны» —— «Некоторые свидетельские показания не являются достоверными».

Превращению подлежат все четыре вида суждений по объединенной классификации: А? Е; Е? А; I?О; О ? I.

Как видим, для превращения суждения необходимо заменить его связку на противоположную, а предикат - на понятие, противоречащее предиката исходного суждения.

Смысл превращения заключается в следующем: заключение, полученное посредством превращения, уточняет наше знание. Устанавливая отношения между субъектом и понятием, противоречащим предикату исходного сужде­ния, мы рассматриваем предмет суждения с новой стороны, фиксируя внимание на свойстве, несовместимом со свойством, отраженным в предикате исходного суждения. Это знание выражает тот факт, что предмет, рассмат­риваемый в одно и то же время, в одном и том же отношении, не может иметь и вместе с тем не иметь одно и то же свойство. Поэтому заключение, полученное с помощью этой логической операции, содержит некоторое но­вое знание о предмете.

Обращение - непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества суждения.

Обращение подчиняется правилу распределенности терминов: субъект распределен в общих и не распределен в частных суждениях, предикат рас­пределен в отрицательных и не распределен в утвердительных суждениях. В соответствии с этим правилом суждения, различные по количеству и каче­ству, обращаются следующим образом:

Все S есть Р ? Некоторые Р есть S

Например: «Все студенты первого курса сдали зачет по логике» ?«Некоторые, сдавшие зачет по логике, - студенты первого курса».

Ни одно S не есть Р? Ни одно Р не есть S

Например: «Ни один студент второй учебной группы не является неуспе­вающим» ? «Ни один неуспевающий не является студентом второй учебной группы».

Некоторые S есть Р? Некоторые Р есть S

Например: «Некоторые женщины - юристы» ? «Некоторые юрис­ты - женщины».

Частноотрицательные суждения не обращаются. Следовательно, обращению подлежат: А ?I; Е? Е; I? I

Смысл обращения состоит в следующем: используя этот логический при­ем, мы уточняем наши знания об объеме предиката суждения и его отноше­нии к субъекту, так как объектом нашей мысли становится предмет, отра­женный предикатом исходного суждения.

Противопоставление предикату - непосредственное умозаключение, ко­торое предполагает получение заключения, где субъектом является понятие, противоречащее предикату исходного суждения, а предикатом является субъект исходного суждения. Нетрудно заметить, что данный вид умозаклю­чения можно рассматривать как результат превращения и обращения:

- превращая исходное суждение «S есть Р», устанавливаем отношение S к не-Р;

- суждение, полученное путем превращения, обращается, в результате устанавливается отношение не-Р к S.

Заключение, полученное путем противопоставления предикату, зависит от количества и качества исходного суждения. В соответствии с этим данный вид непосредственного умозаключения осуществляется следующим образом:

Все S есть Р ? Ни одно не-Р не есть S

Например, «Все адвокаты имеют юридическое образование» ? «Ни один не имеющий юридического образования не является адвокатом».

Ни одно S не есть Р? Некоторые не-Р есть S

Например, «Ни одно предприятие нашего города не является рентабель­ным» ? «Некоторые нерентабельные предприятия являются предприя­тиями нашего города».

Некоторые S не есть Р ? Некоторые не-Р есть S

Например, «Некоторые студенты не являются отличниками» ? «Не­которые неотличники - студенты».

Частноутвердительные суждения посредством противопоставления пре­дикату не преобразуются.

Смысл умозаключений посредством противопоставления предикату со­стоит в том, что в них выясняется отношение предметов, не входящих в объ­ем предиката, к предметам, отраженным субъектом исходного суждения. Устанавливая отношение между этими предметами, мы уточняем наши зна­ния, высказываем нечто новое, что не было в явной форме выражено в ис­ходном суждении.

Умозаключение по логическому квадрату - это такой вид непосредствен­ных умозаключений, который позволяет получать вывод, учитывая свойства отношений между категорическими суждениями А, Е, I, О. Отношения между данными суждениями иллюстрированы схемой логического квадрата. При этом устанавливается следование истинности или ложности одного суждения из истинности или ложности другого суждения в соответствии с теми логическими законами, которые проявляют себя в соответствующих отношениях. В общем виде это можно представить таким образом:

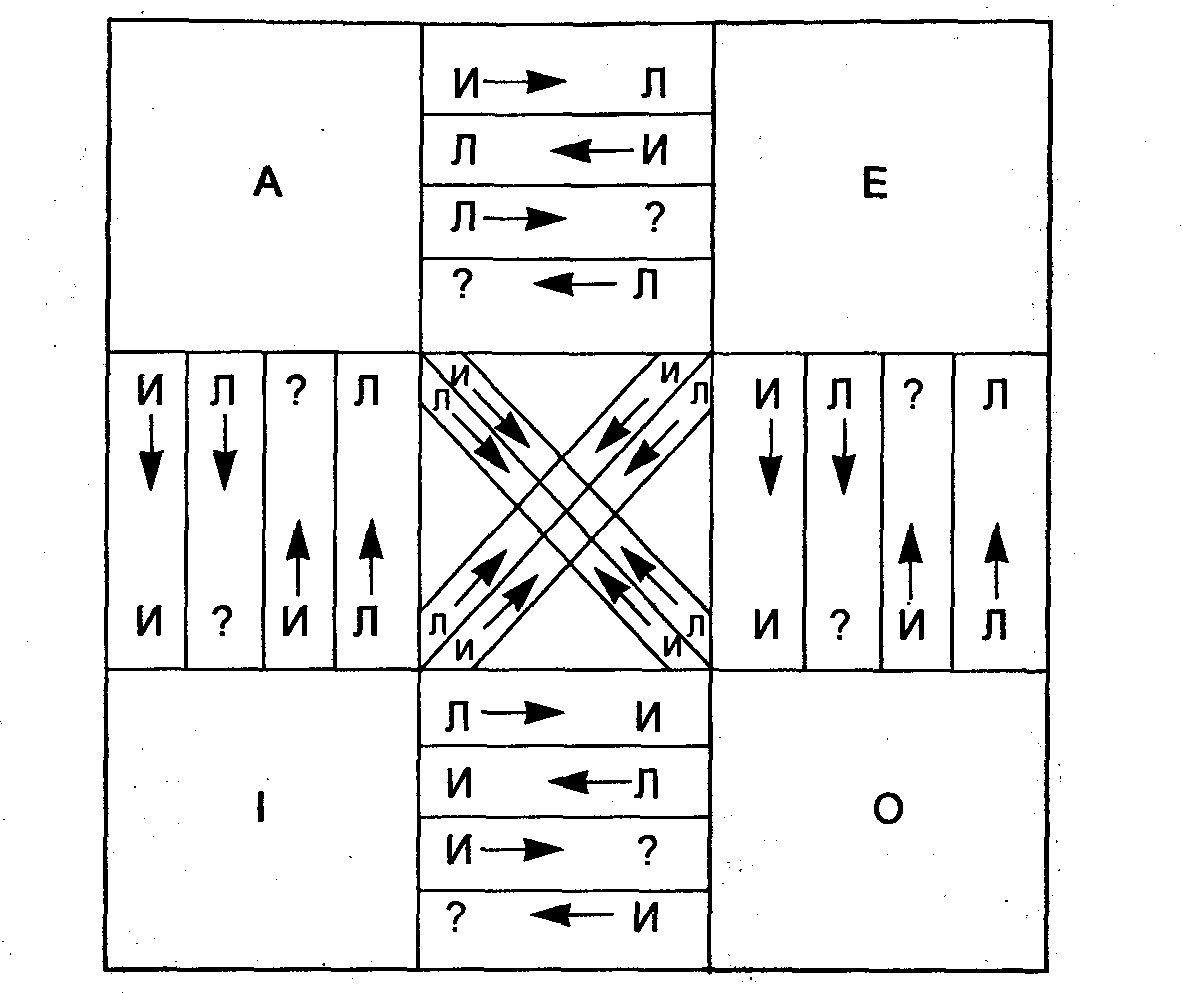
Обозначения на схеме: И - истинность; Л - ложность; ? - неопределенность.

Стрелка указывает направление движения мысли.

Например, пусть дана истинная посылка А: «Все войны есть продолжение политики». Из нее следуют выводы:

1) Е - «Ни одна война не является продолжением политики» - ложный;

2) I - «Некоторые войны являются продолжением политики» - истинный;

3) О - «Некоторые войны не являются продолжением политики» - лож­ный.

Смысл умозаключений по логическому квадрату состоит в том, что зна­ние зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рас­суждения. Эти выводы основаны на определенных правилах, нарушение ко­торых приводит к ошибкам, выражающимся в том, что ложные суждения принимаются за истинные, а истинные за ложные.