ГЛАВА 5. ОБЪЕКТЫ, НАХОДЯЩИЕСЯ ОДНОВРЕМЕННО В ДВУХ МЕСТАХ, И СЛЕДСТВИЯ, КОТОРЫЕ ПРЕДШЕСТВУЮТ СВОИМ ПРИЧИНАМ
ГЛАВА 5. ОБЪЕКТЫ, НАХОДЯЩИЕСЯ ОДНОВРЕМЕННО В ДВУХ МЕСТАХ, И СЛЕДСТВИЯ, КОТОРЫЕ ПРЕДШЕСТВУЮТ СВОИМ ПРИЧИНАМ
Фундаментальные принципы материального реализма просто не подтверждаются. Вместо причинного детерминизма, локальности, строгой объективности и эпифеноменализма квантовая механика предлагает вероятность и неопределенность, корпускулярно-волновую дополнительность, нелокальность и смешение субъектов и объектов.
Возражая против вероятностной интерпретации квантовой механики, порождающей неопределенность и дополнительность, Эйнштейн обычно заявлял, что «Бог не играет в кости». Чтобы понять, что он имел в виду, представьте себе, что вы проводите эксперимент с образцом радиоактивного вещества, распад которого, разумеется, подчиняется вероятностным квантовым законам. Ваша задача состоит в том, чтобы измерять время, в течение которого происходят десять событий радиоактивного распада — десять щелчков вашего счетчика Гейгера. Предположите, что десять событий распада происходят примерно за полчаса. За этим средним значением прячется вероятность. Некоторые серии занимают 32 минуты, другие 25 минут и т.д. Дело еще более осложняется тем, что вам необходимо успеть на автобус, чтобы встретиться со своей возлюбленной, которая терпеть не может, когда ее заставляют ждать. И догадайтесь, что происходит? Ваша последняя серия занимает сорок минут, поскольку случайный распад единичного атома происходит не так, как это выглядело в среднем. Поэтому вы опаздываете на автобус, ваша возлюбленная порывает с вами, и ваша жизнь разрушена. Возможно, это отчасти глупый и надуманный пример того, что происходит в мире, где Бог играет в кости, но он весьма показателен: на вероятностные события можно полагаться только в среднем.
Случайность атомных событий — так сказать, капризность судьбы — несовместима с детерминизмом. Детерминист думает о вероятности так, как о ней принято думать в классической физике и в повседневной жизни: это свойство больших совокупностей объектов — совокупностей столь больших и сложных, что на практике мы не можем их предсказывать, хотя в принципе такое предсказание возможно. Для детерминиста вероятность — это просто удобство мышления: физические законы, управляющие движениями отдельных объектов, являются полностью определенными, и потому, полностью предсказуемыми. Эйнштейн полагал, что так обстоит и с квантово-механической вселенной. За квантовыми неопределенностями стоят скрытые переменные. Вероятности квантовой механики нужны просто для удобства. Будь это так, квантовая механика была бы теорией совокупностей. Действительно, если бы не применяли вероятностное волновое описание к единичному квантовому объекту, то не сталкивались бы с волнующими нас парадоксами — корпускулярно-волновой дополнительностью и неотделимостью квантового объекта от обстоятельств его наблюдения.
К сожалению, все не так просто. Рассмотрение двух квантово-механических экспериментов покажет, как трудно дать рациональное объяснение парадоксов квантовой физики.
Двухщелевой эксперимент
Мы никогда не можем видеть волновой аспект единичной частицы. Всякий раз, когда мы смотрим, нашему взгляду предстает лишь локализованная частица. Должны ли мы, поэтому, допускать, что решение представляет собой трансцендентную метафизику? Или нам следует отказаться от мысли о существовании волнового аспекта единичной волночастицы? Быть может, волны, с которыми имеет дело квантовая физика, — это свойство, присущее только группам или совокупностям объектов?
Чтобы определить, так ли это, мы можем проанализировать эксперимент, обычно используемый для изучения волновых явлений, — так называемый двухщелевой эксперимент. В обстановке этого эксперимента поток электронов проходит через перегородку с двумя узкими щелями (см. рис. 14). Поскольку электроны — это волны, двухщелевая перегородка делит электронный луч на два набора волн. Затем эти волны интерферируют друг с другом, и экспериментаторы видят результат интерференции на флуоресцентном экране.
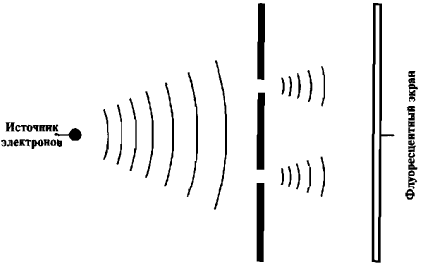
Рис. 14. Двухщелевой эксперимент для электронов
Довольно просто? Позвольте мне рассмотреть феномен интерференции волн. Если вы не знакомы с явлением интерференции, его можно легко продемонстрировать, стоя в ванне, наполненной водой, и ритмично маршируя на месте, в результате чего возникают две серии волн на воде. Волны будут создавать интерференционную картину (рис. 15, а). В одних местах они будут усиливать друг друга (рис. 15, б), а в других — взаимно уничтожаться (рис. 15, в). В результате возникает интерференционная картина.
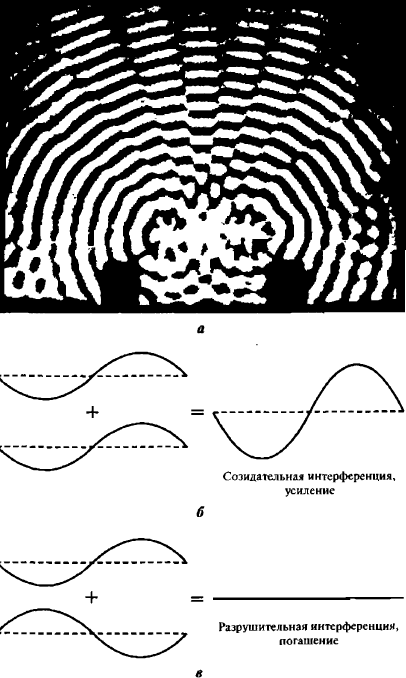
Рис. 15. а — когда волны на воде интерферируют, создается интересная картина взаимных усилений и погашений; б — когда волны приходят в одной фазе, они усиливают друг друга; в — волны, приходящие в противофазе, погашают друг друга
Точно так же на флуоресцентном экране есть места, куда волны электронов от обеих щелей приходят в одной фазе; в таких местах их амплитуды складываются, и суммарная волна усиливается. Между этими яркими пятнышками имеются места, куда волны приходят в противофазе и погашают друг друга. Таким образом, результат этой созидательной и разрушительной интерференции выглядит на экране как узор из чередующихся светлых и темных полос — интерференционная картина (рис. 16). При этом важно, что интервалы между полосами позволяют измерять длину волны электронных волн.
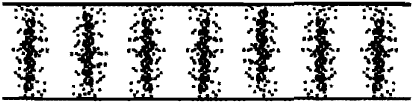
Рис. 16. Интерференционная картина вспышек на экране
Однако вспомним, что волны электронов представляют собой волны вероятности. Поэтому мы должны говорить именно о вероятности: электроны, попадающие в светлые области, имеют высокую вероятность, а электроны, попадающие в темные области, — низкую вероятность. Мы не должны увлекаться и на основании интерференционной картины делать вывод, что волны электронов — это классические волны, поскольку электроны все же попадают на флуоресцентный экран так, как это положено частицам: каждый электрон дает одну локализованную вспышку. Именно совокупность пятен, образованных большим числом электронов, выглядит как картина интерференции волн.
Предположим, что мы идем на интеллектуальный риск и делаем электронный луч очень слабым — настолько слабым, что в любой данный момент щелей достигает только один электрон. Получаем ли мы по-прежнему интерференционную картину? Квантовая механика однозначно отвечает — да. Вы можете возразить — нельзя получить интерференцию без разделения луча. Разве для интерференции нужны не две волны? Может ли единичный электрон разделяться, проходить через обе щели и интерферировать сам с собой? Да, может. Квантовая механика отвечает на все эти вопросы положительно. По словам одного из пионеров новой физики, Поля Дирака: «Каждый фотон (или, в данном случае, электрон) интерферирует только сам с собой». Квантовая механика предлагает математическое доказательство этого абсурдного утверждения, но это единственное утверждение ответственно за всю удивительную магию, на которую способны квантовые системы и которая подтверждена множеством экспериментов и технологий.
Попробуйте представить себе, что электрон проходит на 50% через одну щель и на 50% через другую щель. Легко рассердиться и не верить в это странное следствие квантовой математики. Действительно ли электрон проходит через обе щели одновременно? Почему мы должны принимать это на веру? Мы можем выяснить это путем наблюдения. Мы можем направить на щели фонарь (метафорически говоря), чтобы видеть, через какую щель электрон проходит на самом деле.
Итак, мы включаем свет и, видя электрон, проходящий через ту или другую щель, смотрим, где на флуоресцентном экране возникает вспышка (рис. 17). Мы обнаруживаем, что каждый раз, когда электрон проходит через щель, его вспышка появляется точно позади щели, через которую он проходит. Интерференционная картина исчезла.
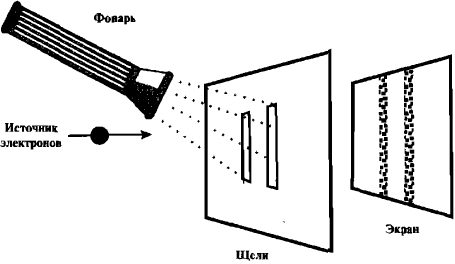
Рис. 17. Когда мы пытаемся определять, через какую щель проходит электрон, направляя на щели фонарь, электрон демонстрирует свою корпускулярную природу. Есть только две полосы — в точности так, как следовало бы ожидать, если бы электроны были миниатюрными шариками
То, что происходит в этом эксперименте, можно понимать, прежде всего, как следствие принципа неопределенности. Как только мы обнаруживаем электрон и определяем, через какую щель он проходит, мы утрачиваем информацию об импульсе электрона. Электроны очень чувствительны; столкновение с фотоном, который мы используем для наблюдения электрона, воздействует на него так, что его импульс меняется на непредсказуемую величину. Импульс и длина волны электрона взаимосвязаны: квантовая механика включает в себя это великое открытие де Бройля. Поэтому утрата информации об импульсе электрона — это то же самое, что утрата информации о его длине волны. Если бы имелись интерференционные полосы, то мы могли бы измерять длину волны по расстояниям между ними. Принцип неопределенности утверждает, что как только мы определяем, через какую щель проходит электрон, процесс наблюдения уничтожает интерференционную картину.
Вы должны понимать, что измерения положения и импульса электрона, в действительности, представляют собой взаимодополнительные, взаимоисключающие процедуры. Мы можем сосредоточиваться на импульсе и измерять длину волны — и, таким образом, импульс — электрона по интерференционной картине, но тогда мы не можем знать, через какую щель проходит электрон. Или мы можем сосредоточиваться на положении электрона и терять интерференционную картину — информацию о его длине волны и импульсе.
Существует второй, еще более хитроумный способ понимания и согласования всего этого — с помощью принципа дополнительности. В зависимости от того, какой прибор мы используем, мы видим корпускулярный аспект (например, с фонарем) или волновой аспект (без фонаря).
В первом приближении суть принципа дополнительности сводится к тому, что квантовые объекты представляют собой и волны, и частицы, но мы можем видеть с помощью той или иной экспериментальной обстановки только один аспект. Это, несомненно, правильное понимание, однако опыт учит нас некоторым тонкостям. Например, мы также должны говорить, что электрон — это не волна (поскольку волновой аспект никогда не проявляется для единичного электрона) и не частица (поскольку он появляется на экране в местах, запрещенных для частиц). Тогда, будучи осмотрительными в своей логике, мы должны говорить и что фотон — это ни не-волна, ни не-частица, чтобы избежать неправильного понимания нашего употребления слов «волна» и «частица». Это очень похоже на логику жившего в I в. н. э. философа-идеалиста Нагарджуны — самого проницательного логика традиции буддизма Махаяны. Восточные философы передают свое понимание окончательной реальности словами нети, нети (ни это, ни то). Нагарджуна сформулировал это учение в виде четырех отрицаний:
Она не существует.
Она не является несуществующей.
О ней нельзя утверждать,
что она и существует и не существует.
Или что она не является ни
существующей, ни несуществующей.
Чтобы лучше понять дополнительность, предположим, что мы возвращаемся к предыдущему эксперименту, на этот раз используя слабые батареи, чтобы сделать фонарь, которым мы освещаем электроны, несколько более тусклым. Повторяя эксперимент, показанный на рис. 17, с все более и более тусклым светом фонаря, мы обнаруживаем, что интерференционная картина начинает снова появляться, делаясь все более отчетливой по мере того, как свет фонаря становится все более тусклым (рис. 18). Когда фонарь совсем выключен, возвращается полная интерференционная картина.

Рис. 18. При использовании более тусклого фонаря отчасти возвращается интерференционная картина
По мере того как фонарь тускнеет, число фотонов, рассеивающих электроны, уменьшается, так что некоторым электронам удается полностью избежать быть «видимыми» посредством света. Те электроны, которые видимы, появляются позади щели 1 или щели 2, именно там, где бы мы ожидали их найти. Каждый из не увиденных электронов разделяется и интерферирует сам с собой, образуя на экране интерференционную картину, когда его достигнет достаточное число электронов. В предельном случае яркого света видна только корпускулярная природа электронов; в предельном случае отсутствия света видна только волновая природа. В промежуточных случаях тусклого света в аналогичной промежуточной степени видны оба аспекта: то есть здесь мы видим электроны (хотя никогда один и тот же электрон) как одновременно и волны, и частицы. Таким образом, волновая природа волночастицы не является свойством всей совокупности, но должна оставаться в силе для каждой индивидуальной волночастицы, когда мы на нее не смотрим. Это должно означать, что волновой аспект единичного квантового объекта трансцендентен, поскольку мы никогда не видим его проявленным.
Происходящее помогает объяснить ряд картинок (рис. 19). На картинке внизу слева мы видим только букву W; это соответствует использованию яркого фонаря, который показывает только корпускулярную природу электронов. Затем, двигаясь вверх от картинки к картинке, мы начинаем видеть орла — точно так же, как при уменьшении яркости света некоторые электроны избегают наблюдения (и локализации), и мы начинаем видеть их волновую природу. Наконец, на последней, верхней правой картинке, можно разглядеть только орла; фонарь выключен, и теперь все электроны представляют собой волны.

Рис. 19. Последовательность W—Орел
Нильс Бор как-то сказал: «Те, кто не испытал шок при первой встрече с квантовой теорией, вероятно, ее не поняли». По мере того как мы начинаем постигать действие принципа дополнительности, этот шок сменяется пониманием. Тогда официальный марш предсказательной науки, справедливой либо для волны, либо для частицы, преобразуется в творческий танец трансцендентной волночастицы. Когда мы локализуем электрон, выясняя, через какую щель он проходит, то открываем его корпускулярный аспект. Когда мы не локализуем электрон, не обращая внимания на то, через какую щель он проходит, то открываем его волновой аспект. В последнем случае электрон проходит через обе щели.
Эксперимент отложенного выбора
Следует ясно понимать это уникальное свойство принципа дополнительности: то, какой атрибут раскрывает квантовая волночастица, зависит от выбираемого нами способа ее наблюдения. Лучше всего важность сознательного выбора в формировании проявленной реальности демонстрирует эксперимент отложенного выбора, предложенный физиком Джоном Уиллером.
На рис. 20 показан прибор, в котором луч света разделяется на два луча равной интенсивности — отраженный и проходящий — с помощью полупрозрачного зеркала М1. Затем оба луча отражаются двумя обычными зеркалами А и В и достигают точки пересечения Р справа.
Для обнаружения волнового аспекта волночастицы мы используем феномен интерференции волн и помещаем в точке Р второе полупрозрачное зеркало М2 (рис. 20, внизу слева). Теперь зеркало М2 заставляет обе волны, создаваемые лучом, который разделяется зеркалом М1 созидательно интерферировать по одну сторону Р (если поместить туда счетчик фотонов, то он будет щелкать) и разрушительно интерферировать по другую сторону (где счетчик никогда не щелкает). Заметьте, что при обнаружении волнового модуса фотонов мы должны признавать, что каждый фотон разделяется в зеркале M1 и движется обоими путями А и В, а иначе как может быть интерференция?
Поэтому когда зеркало M1 разделяет луч, каждый фотон потенциально готов двигаться обоими путями. Если теперь мы решаем обнаруживать корпускулярный модус волночастиц фотонов, мы убираем зеркало М2 из точки Р (чтобы предотвратить рекомбинацию и интерференцию) и помещаем за точкой пересечения Р счетчики, как показано на рис. 20 внизу справа. Тот или другой счетчик будет щелкать, определяя локализованный путь волночастицы — отраженный путь А или проходящий путь В — и демонстрируя корпускулярный аспект.
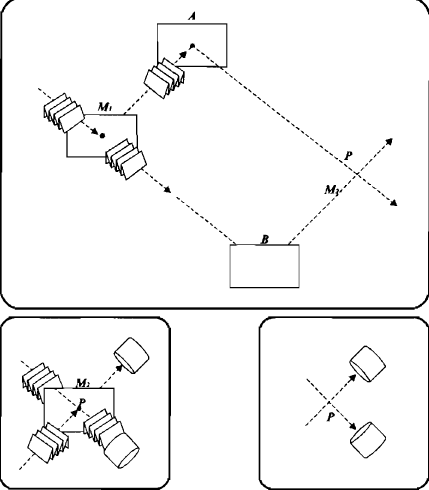
Рис. 20. Эксперимент отложенного выбора. ВНИЗУ СЛЕВА: экспериментальная обстановка для видения волновой природы фотонов. Один из детекторов никогда не обнаруживает никаких фотонов, свидетельствуя о погашении вследствие интерференции волн. Фотон должен был разделиться и проходить по двум путям одновременно. ВНИЗУ СПРАВА: обстановка для видения корпускулярной природы фотонов. Оба детектора щелкают, но попеременно, показывая, по какому пути движется фотон
Самая хитрая часть эксперимента состоит в следующем: в эксперименте отложенного выбора экспериментатор решает, помещать или нет полупрозрачное зеркало в точку Р — измерять или нет волновой аспект, — в самый последний момент, в самую последнюю пикосекунду (10-12 с) (это было реально осуществлено в лаборатории). По существу это означает, что фотоны уже прошли точку разделения (если думать о них как о классических объектах). Даже в таком случае помещение зеркала в точку Р всегда показывает волновой аспект, а не помещение показывает корпускулярный аспект. Двигался ли каждый фотон по одному пути или по двум? По-видимому, фотоны мгновенно и ретроактивно реагируют даже на наш отложенный выбор. Фотон проходит по одному пути или по обоим в точном соответствии с нашим выбором. Каким образом он знает о нем? Предшествует ли во времени следствие нашего выбора своей причине? По словам Джона Уиллера: «Природа на квантовом уровне — это не машина, идущая своим неумолимым путем. Вместо этого ответ, который мы получаем, зависит от того, какой вопрос мы ставим, какой эксперимент мы устраиваем, какой регистрирующий прибор мы выбираем. Мы неизбежно вовлекаемся в вызывание того, что оказывается происходящим».
Не существует никакого проявленного фотона до того, как мы его видим, и потому то, как мы его видим, определяет его атрибуты. До нашего наблюдения фотон разделяется на два волновых пакета (один пакет для каждого из путей), но эти пакеты — только пакеты возможностей для фотона; в M1 нет никакой действительности в пространстве-времени, никакого принятия решения. Предшествует ли следствие своей причине, тем самым нарушая закон причинности? Несомненно, да — если думать о фотоне как о классической частице, всегда проявленной в пространстве-времени. Однако фотон — не классическая частица.
С точки зрения квантовой физики, при помещении второго зеркала в точке Р в нашем эксперименте отложенного выбора оба разделенных пакета потенциально соединяются и интерферируют; тут нет никакой проблемы. Если бы в точке Р было зеркало, и мы убирали его в последнюю возможную пикосекунду, обнаруживая фотон, скажем, на пути А, то казалось бы, что фотон ретроактивно реагирует на наш отложенный выбор, двигаясь только по одному пути. Следовательно, в этом случае казалось бы, что следствие предшествует причине. Этот результат не нарушает закон причинности. Как же так?
Необходимо понимать более тонкий способ рассмотрения второго эксперимента по обнаружению корпускулярного аспекта фотонов; как поясняет Гейзенберг: «Если теперь результат эксперимента свидетельствует о нахождении фотона, скажем, в отраженной части [волнового] пакета [путь А], то вероятность обнаружения фотона в другой части луча немедленно становится равной нулю. Тогда эксперимент с положением отраженного пакета оказывает своего рода действие... в отдаленной точке, занимаемой проходящим пакетом, и наблюдатель видит [что] это действие распространяется со скоростью, превышающей скорость света. Однако очевидно также, что этот вид действия никогда не может быть использован для передачи сигнала, так что он... не противоречит постулатам теории относительности».
Это действие на расстоянии составляет важный аспект коллапса («схлопывания») волнового пакета. Для обозначения такого действия используется специальный термин нелокалъностъ — действие, передаваемое без сигналов, которые распространяются в пространстве. Сигналы, которые распространяются в пространстве за конечное время, вследствие установленного
Эйнштейном предела скорости, называются локальными сигналами. Поэтому коллапс квантовой волны не локален.
Отметьте, что утверждение Гейзенберга справедливо и при наличии, и при отсутствии отложенного выбора. С квантовой точки зрения важно то, что мы выбираем тот или иной исход, который и проявляется; когда во времени мы выбираем этот исход, не имеет значения. Волна разделяется всякий раз, когда есть два доступных пути, но разделение происходит только в потенции. Когда, позднее, мы наблюдаем фотон на одном пути, потому что выбираем такой исход (удаляя зеркало из точки Р), вызываемое нами «схлопывание» волны на одном пути оказывает на волну на другом пути нелокальное влияние, которое сводит на нет возможность видения фотона на этом другом пути. Подобное нелокальное влияние может показаться ретроактивным (т. е. передающимся назад во времени), однако мы влияем только на потенциальные возможности; здесь нет никакого нарушения закона причинности, поскольку, как говорит Гейзенберг, мы не можем передавать сигнал с помощью такого рода устройства[26].
В своем поиске смысла и структуры реальности мы сталкиваемся с той же загадкой, с которой столкнулся Винни-Пух:
— Привет, Пух, —сказал Пятачок, — что это ты делаешь ?
— Охочусь, - сказал Пух.
— Охотишься ? На кого ?
— Кое-кого выслеживаю, — ответил Винни-Пух очень таинственно.
— Кого выслеживаешь? — спросил Пятачок, подходя ближе.
— Именно об этом я сам себя спрашиваю. В этом весь вопрос — кого ?
— И как ты думаешь, что ты ответишь на этот вопрос ?
— Придется подождать, пока я его догоню, — сказал Винни-Пух.
— Взгляни-ка сюда. — Он показал на землю прямо перед собой. — Что ты тут видишь?
— Следы, — сказал Пятачок. — Отпечатки лап! — Он даже слегка взвизгнул от волнения.
— Ой, Пух! Ты думаешь, это... это страшный Бука?
— Может быть, — сказал Пух. — Иногда как будто он, а иногда как будто и не он. По следам разве угадаешь?..
— ...Минуту, — сказал Винни-Пух, подняв лапу. Он сел и задумался так глубоко, как только мог. Потом он примерил свою лапу к одному из Следов... а потом дважды почесал за ухом и встал. — Да, — сказал Винни-Пух. — Теперь я понял. Я был глупым простофилей, — сказал он.
— И я самый бестолковый медвежонок на свете!
— Что ты! Ты самый лучший медвежонок на свете! — утешил его Кристофер Робин.
Действительно, несколько озадачивает то, что согласно новой физике, следы «буки», которые оставляют электрон и другие субмикроскопические частицы в наших конденсационных камерах, — это просто расширение нас самих.
Классическая наука неизменно видела в мире только разделенность. Два века назад английский поэт-романтик Уильям Блейк писал:
Храни нас Бог от единообразного видения и ньютоновского сна.
Квантовая физика — это ответ на молитву Блейка. Современный ученый, усвоивший урок принципа дополнительности, не настолько глуп, чтобы «зацикливаться» на (кажущейся) разделенности.
Квантовые измерения выводят наше сознание на сцену так называемого объективного мира. В эксперименте отложенного выбора нет никакого парадокса, если мы отказываемся от представления о том, что неизменный и независимый мир существует, даже когда мы его не наблюдаем. В конечном счете все сводится к тому, что вы, наблюдатель, хотите видеть. Это напоминает мне об одной дзэнской истории.
Два монаха спорили о движении флага на ветру Один говорил: «Флаг движется». Другой возражал: «Нет, это ветер движется». Третий монах, проходивший мимо спорщиков, высказал замечание, которое бы одобрил Уиллер: «Флаг не движется. Ветер не движется. Движется ваш ум».
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Глава 2. О гордости и униженности. Их объекты и причины
Глава 2. О гордости и униженности. Их объекты и причины Так как аффекты гордости и униженности 2 — простые и единообразные впечатления, то мы совершенно не в состоянии дать точное определение как этих, так, собственно, и других аффектов при помощи ряда слов. Самое большее,
ТЕ, КОТОРЫЕ ЗНАЮТ, И ТЕ, КОТОРЫЕ ВЕРЯТ
ТЕ, КОТОРЫЕ ЗНАЮТ, И ТЕ, КОТОРЫЕ ВЕРЯТ Но существует и еще одна великая узурпация: та, которую совершила религия — в узком и современном смысле этого слова — узурпация области «священного» и «божественного».Священное и божественное — это предмет веры: эта истина была
8. Характеристика двух типов онтологических суждений, которые могут скрываться в свободном от оценки понятии идеологии
8. Характеристика двух типов онтологических суждений, которые могут скрываться в свободном от оценки понятии идеологии После нашего экскурса в ex-post[53] онтологию[54] и позитивизм (он был необходим для правильного понимания того движения мысли, которое мы рассматриваем ниже,
3. Основные формы, находящиеся в связи с фихтевской философией
3. Основные формы, находящиеся в связи с фихтевской философией Что касается содержания, которое «я» получает в философии Фихте, то, с одной стороны, слишком уж бросались в глаза его полнейшая бездуховность, деревянность и (чтобы сказать настоящее слово) нелепость, чтобы
Объекты информационные и объекты физические
Объекты информационные и объекты физические Как, собственно, понимать, что «передача информации — статистический процесс»? Отчего мы неоднократно возвращались к этому аспекту процессов передачи информации и повторно употребляли изжитый термин «стохастический» или
СТАНЦА III (продолжение) Шлока (2) ТРЕПЕТ РАСПРОСТРАНЯЕТСЯ, КАСАЯСЬ СВОИМ СТРЕМИТЕЛЬНЫМ КРЫЛОМ (одновременно) ВСЕЙ ВСЕЛЕННОЙ И ЗАРОДЫША, ПРЕБЫВАЮЩЕГО ВО ТЬМЕ, КОТОРАЯ ДЫШИТ (движется) НАД ДРЕМЛЮЩИМИ ВОДАМИ ЖИЗНИ
СТАНЦА III (продолжение) Шлока (2) ТРЕПЕТ РАСПРОСТРАНЯЕТСЯ, КАСАЯСЬ СВОИМ СТРЕМИТЕЛЬНЫМ КРЫЛОМ (одновременно) ВСЕЙ ВСЕЛЕННОЙ И ЗАРОДЫША, ПРЕБЫВАЮЩЕГО ВО ТЬМЕ, КОТОРАЯ ДЫШИТ (движется) НАД ДРЕМЛЮЩИМИ ВОДАМИ ЖИЗНИ ВОПРОС — Как следует понимать выражение, что трепет касается
Глава 8 Причины и следствия
Глава 8 Причины и следствия Система Спинхемленда была задумана, в сущности, как временная мера, однако немногие институты оказали столь же определяющее влияние на судьбу целых цивилизаций, как этот эксперимент, отвергнутый ради того, чтобы могла начаться новая эра. Он был
10.6. Эсхатология в других местах?
10.6. Эсхатология в других местах? Но есть ли в других местах что?нибудь, кроме безжизненных планет, солнц и облаков пыли? Большинство современных биологов знакомы с парадоксом Ферми, утверждающим, что, если бы внеземная разумная жизнь существовала, мы бы уже о ней знали — не
Глава двадцать первая О СВОЙСТВАХ, КОТОРЫЕ ВЕЩИ ИМЕЮТ ПРИ ЖИЗНИ, И СВОЙСТВАХ, КОТОРЫЕ ИМ ОСТАЮТСЯ ПОСЛЕ СМЕРТИ
Глава двадцать первая О СВОЙСТВАХ, КОТОРЫЕ ВЕЩИ ИМЕЮТ ПРИ ЖИЗНИ, И СВОЙСТВАХ, КОТОРЫЕ ИМ ОСТАЮТСЯ ПОСЛЕ СМЕРТИ Еще нужно знать, что есть некоторые свойства, которые сохраняются только в течение их жизни, и что есть другие, некоторые свойства, которые пребывают в них даже
Глава 6. Другие свидетельства Священного Писания о Святой Троице. Различие Приказывающего и Исполняющего не вводит Двух Богов и Двух Господов
Глава 6. Другие свидетельства Священного Писания о Святой Троице. Различие Приказывающего и Исполняющего не вводит Двух Богов и Двух Господов 12. А если тебя все еще смущает число Троицы, словно [ее Лица] не связаны друг с другом в простом единстве, я спрашиваю [тебя], каким
Одна частица — сразу в двух местах?
Одна частица — сразу в двух местах? В приведенном выше описании я избрал гораздо более «реалистическую» точку зрения на волновую функцию, чем та, которая обычно принята среди квантовых физиков. Я придерживаюсь точки зрения, согласно которой «объективно реальное»
Глава V. Как управлять городами или государствами, которые, до того как были завоеваны, жили по своим законам
Глава V. Как управлять городами или государствами, которые, до того как были завоеваны, жили по своим законам Если, как сказано, завоеванное государство с незапамятных времен живет свободно и имеет свои законы, то есть три способа его удержать. Первый – разрушить; второй –