в) Аксиомы и постулаты как основания доказательства

в) Аксиомы и постулаты как основания доказательства

Положения об удостоверенных фактах и определения входят в число оснований самых различных наук: естественных и общественных.

В математике, механике и теоретической физике кроме определений и удостоверенных фактов в число оснований доказательства входят ещё аксиомы, или постулаты. Так называются положения, которые предполагаются истинными, но в пределах каждой науки в качестве истинных не доказываются.

Так, доказательство теоремы евклидовой геометрии о равенстве суммы внутренних углов плоского треугольника двум прямым опирается не только на ранее доказанную теорему о равенстве суммы двух смежных углов двум прямым, но, кроме того, на теоремы о свойствах внутренних накрест лежащих и соответственных углов, которые в свою очередь опираются на положение, согласно которому через данную точку вне данной прямой в одной с ней плоскости можно провести одну — и притом только одну — прямую, которая ни при каком продолжении её в обе стороны от данной точки не пересечётся с данной прямой. Положение это уже не теорема, а аксиома (постулат). В «Началах» Евклида оно дано (в редакции, отличающейся от приведённой в тексте) в качестве 11-й аксиомы первой книги[16].

Аксиомой (постулатом) это положение является потому, что в «Началах» Евклида оно принимается без доказательства. И действительно: положение это утверждает, что возможно неограниченно продолжить прямую так, чтобы последняя нигде не пересекалась с данной прямой. Но совершенно очевидно, что утверждение это не может быть проверено или доказано: как бы далеко мы ни продолжали прямую, продолжение её будет для нашего наглядного представления ограниченным. В лучшем случае можно сказать, что в тех пределах, в каких прямая продолжена нами, она сохраняет параллельность данной прямой. Но сохранит ли она параллельность и при дальнейшем, ещё нами не воспринятом неограниченном её продолжении,— это остаётся недоказанным.

Аристотель, создавший не только науку логики в целом, но и разработавший, в частности, логическое учение о доказательстве, отличал аксиомы от другого вида недоказываемых наукой положений — от постулатов. Под аксиомами (???????) он разумел такие недоказываемые в данной науке положения, которые в сравнении с другими недоказываемыми положениями являются, во-первых, наиболее общими и, во-вторых, представляют необходимое условие доказательства. Так, в «Метафизике» (кн. III, гл. 2, 997а 5—13) Аристотель говорит, что «не может существовать доказательства для всего», что «все доказывающие науки применяют аксиомы» и что «аксиомы обладают наивысшей степенью общности и представляют начала всего» (??????? ??? ??????? ?? ?????? ????? ?? ???????? ?????).

Под постулатами (?? ????????, буквально — «требования») Аристотель понимал такие положения, которые, безотносительно к их доказуемости, вводятся в начала науки без доказательства, хотя бы они представлялись учащемуся противными его мнению[17]. Именно потому, что постулат может быть противным мнению учащегося, он вводится в качестве требования: это — положение, которое должно быть принято для того, чтобы были приняты все вытекающие из него выводы.

Постулаты Аристотель отличал от аксиом, но не противопоставлял их аксиомам.

В развитии античной математики после Аристотеля были выработаны три точки зрения по вопросу о различии между аксиомами и постулатами. Эти три точки зрения рассматривает математик и философ Прокл (V век н. э.) в своих «Комментариях» к «Началам» Евклида.

Согласно первой из этих точек зрения, аксиомы — не- доказываемые положения, на которые опираются доказательства теорем, а постулаты — недоказываемые положения, на которые опираются построения в геометрии.

Согласно второй точке зрения, аксиомы — допущения, общие для всех наук, а постулаты — специальные допущения, принятые в геометрии. Так, у Евклида в качестве аксиом рассматривались, например, такие положения: «равные одному и тому же равны и между собой», «если к равным прибавляются равные, то и целые будут равные» и т. д. В качестве постулатов у Евклида рассматриваются, например, такие положения: «от всякой точки до всякой точки <можно> провести прямую линию», «из всякого центра и всяким раствором <циркуля> <может быть> описан круг» и т. д.

Зачатки этого понимания различия между аксиомами и постулатами имелись уже у Аристотеля: «Из тех <на- чал>,— читаем у Аристотеля,— которые применяются в доказывающих науках, одни свойственны каждой науке в отдельности, другие — общи всем...»[18].

Согласно третьей точке зрения, постулаты — в отличие от аксиом — суть «требования», выдвигаемые преподающим науку или руководителем диспута. Постулаты должны быть приняты учащимися или участниками диспута, несмотря на то, что для них требования эти могут представляться не безусловно бесспорными[19].

Впоследствии возобладал взгляд, согласно которому аксиомами должны называться недоказываемые положения не специальные, имеющие силу для всех наук, постулатами же — недоказываемые положения более частные, относящиеся к области какой-нибудь особой специальной науки. Согласно этому взгляду, положение о том, что две величины, равные порознь третьей, равны между собой, рассматривалось в силу его всеобщности как типичная аксиома. Напротив, положение о параллельных вследствие его специально геометрического характера толковалось как типичный постулат.

Распределение аксиом и постулатов в «Началах» Евклида не вполне соответствует этому различению. Хотя ряд постулатов Евклида принадлежит к области геометрия, а ряд его аксиом — к области более общего учения о величинах, последовательное разграничение аксиом и постулатов по степени их специального характера оказывается невозможным. Так, 7-я аксиома первой книги «Начал», утверждающая, что «совмещающиеся друг с другом равны между собой», есть, конечно, аксиома геометрии. Положение о параллельных, принадлежащее к области геометрии, помещалось Евклидом в числе аксиом (11-я аксиома первой книги«Начал») и только позднейшими комментаторами и издателями стало рассматриваться как постулат (5-й постулат той же книги).

В философии и математике XVII века понимание логической природы аксиом и постулатов изменилось. Ряд математиков и логиков этого века сущность аксиом стал видеть в их будто бы безусловной очевидности или самоочевидности. Согласно этому новому взгляду, аксиомы — такие основания доказательства, которые не доказываются в науке не в силу своей общепринятости, а в силу своей полной и безусловной очевидности. Существуют будто бы такие положения, которые, как только на них направляется наш ум, представляются ему с ясностью и очевидностью, исключающими возможность какого бы то ни было сомнения. Будучи совершенно очевидными, положения эти будто не требуют доказательства, ниоткуда не выводятся, представляют истины, непосредственно постигаемые умом, или, другими словами, являются «интуициями», притом интуициями не чувств, а ума. Аксиомы—не просто недоказываемые истины, какими их считали древние математики. Это — истины будто бы недоказуемые. Не нуждаясь ни в каком доказательстве, они составляют последнюю основу всех доказываемых в науке истин. Доказать — значит вывести доказываемое положение или прямо из таких самоочевидных аксиом, или вывести его из положений, которые если не прямо, то в последней инстанции сами опираются на самоочевидные аксиомы и доказываются с их помощью.

В этом учении существенным признаком аксиом провозглашается их непосредственно постигаемая самоочевидность (интуитивность) и их недоказуемость. Напротив, их общепризнанность и более или менее общий для всех наук или специальный характер получает значение свойства, производного от указанных основных свойств.

В связи с этим характерное для античных логиков и математиков понимание различия между постулатами и аксиомами у логиков и математиков XVII века в значительной мере утрачивает прежнее значение. Возникает тенденция к сближению постулатов с аксиомами. Поскольку некоторые постулаты представляются не менее очевидными, чем аксиомы, и поскольку непосредственная очевидность аксиом рассматривается как основание их недоказуемости, такие постулаты по сути уже не отличаются от аксиом и вместе с аксиомами образуют совокупность последних оснований всякого доказательства.

В то же время, однако, некоторые постулаты не поддавались этому сближению с аксиомами по признаку безусловной очевидности. Таков был прежде всего постулат

Евклида о параллельных. Уже в самой своей формулировке он содержал понятие о неограниченном продолжении прямой — понятие, которое никак не могло быть признано ни самоочевидным, ни непосредственно постигаемым.

К этому присоединилось ещё и то, что целый ряд начальных положений (теорем и задач на построение) геометрии Евклида доказывался и решался вовсе без участия постулата о параллельных. Только в двадцать девятом предложении первой книги «Начал» постулат Евклида впервые использовался в качестве одного из оснований доказательства этого предложения.

Эта далеко не безусловная «очевидность» постулата о параллельных, а также «позднее» появление его в числе оснований, на которые опираются доказательства теорем геометрии Евклида, в сопоставлении со взглядом на аксиомы, как на истины самоочевидные, уже давно внушали математикам мысль — не является ли этот постулат теоремой, которая может быть доказана.

Попытки доказать 5-й постулат Евклида предпринимались ещё античными математиками и продолжались до Лобачевского. Великий русский математик во второй половине 20-х годов прошлого века пришёл к гениальному открытию, которое повлекло за собой коренную переработку взгляда логики на природу аксиом и на их значение для доказательства.

В начале своих исследований, посвящённых теории параллельных, Лобачевский пытался доказать постулат Евклида способом от противного. Предполагая, в противоречии с постулатом Евклида, что через точку вне данной прямой в одной с ней плоскости можно провести не одну единственную прямую, не пересекающуюся с данной, Лобачевский надеялся, что, развивая следствия из этого предположения, он придёт в конце концов к следствию, опровергающему это предположение и тем самым доказывающему истинность самого постулата Евклида.

Но никакие следствия, развиваемые из предположения, противоречащего постулату Евклида, не могли доказать абсурдность этого предположения. Никаких противоречий между теоремами, доказанными на основе предположения, противоречащего постулату Евклида, не получалось.

В конце концов Лобачевский убедился, что все старания ряда математиков доказать постулат Евклида, т. е. вывести его как следствие из других аксиом и постулатов

Евклида, были ошибочны не только по выполнению, но и по замыслу. Постулат о параллельных оказался независимым от остальных аксиом и постулатов Евклида. С другой стороны, как уже говорилось выше, постулат этот не обладает и безусловной очевидностью. Тем не менее постулат Евклида является одним из оснований классической системы геометрии, не заключающей нигде в своих доказываемых с помощью этого постулата положениях никаких противоречий.

Небезусловная очевидность постулата Евклида и отсутствие противоречий в системе теорем, доказываемых на основе постулата, противоречащего постулату о параллельных, даёт возможность поставить вопрос, каков будет результат, если вместо постулата Евклида в число оснований геометрии будет принят другой — тоже не безусловно очевидный — постулат. Согласно последнему, получившему название постулата Лобачевского, через данную точку С, лежащую вне данной прямой АВ, можно провести в одной с ней плоскости не . одну единственную не пересекающуюся с прямой АВ прямую, как это утверждает постулат Евклида, а целый пучок прямых, заключающийся между двумя прямыми KL и MN, проходящими через данную точку (см. рис.1) и называемыми параллельными относительно АВ[20].

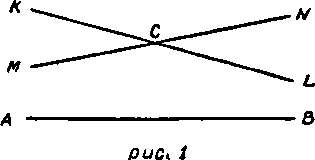
Исследования Лобачевского показали, что замена постулата Евклида постулатом Лобачевского приводит к выявлению новой системы геометрии, получившей название геометрии Лобачевского и оказавшейся одним из видов так называемой неевклидовой геометрии. В геометрии Лобачевского сохраняются все определения, аксиомы и постулаты геометрии Евклида, кроме 5-го постулата, или 11-й аксиомы. Последний заменяется постулатом Лобачевского. Доказательства теорем развиваются безупречно строго в полную систему геометрии, которая нигде не приводит ни к каким противоречиям. По содержанию теоремы геометрии Лобачевского делятся на два класса: во-первых, теоремы, доказываемые без помощи постулата Лобачевского (так называемая абсолютная геометрия), и, во-вторых, теоремы, доказываемые с помощью этого постулата. Первые ничем не отличаются от соответствующих теорем Евклида. Вторые отличаются, а именно: разность в численных результатах этих теорем сравнительно с результатами теорем Евклида тем больше, чем больше масштаб соответствующего геометрического объекта. Например, по Евклиду, сумма внутренних углов плоского треугольника равна двум прямым. По Лобачевскому, эта сумма меньше двух прямых. При этом разность эта тем больше, чем больше данный треугольник.

Открытие Лобачевским неевклидовой геометрии означало эпоху не только в развитии математики, но также и в развитии логического учения об аксиомах как об основаниях доказательства. Это открытие Лобачевского нанесло смертельный удар идеалистическим теориям рационалистов и кантианцев. Логики этого направления сущность аксиом полагали в их интуитивной, т. е. непосредственной очевидности, в их априорной, т. е. будто бы предшествующей всякому опыту, безусловной и необходимой наглядности. Так как, по Канту, истины математики имеют, во-первых, всеобщий и необходимый характер, во- вторых, основываются на априорных формах чувственной интуиции, то ни о какой неевклидовой геометрии, разумеется, не может быть и речи.

Напротив, по Лобачевскому, вопрос о том, какие аксиомы или постулаты должны быть приняты в число оснований всей системы доказательств данной науки, определяется отнюдь не априорными формами интуиции. Такие положения геометрии, как постулат Евклида или постулат Лобачевского, отнюдь не безусловно самоочевидны.

Так как аксиомы не обладают безусловной очевидностью, то для решения вопроса о том, какие из небезусловно очевидных положений будут в данной науке доказываться, а какие будут приняты в ней без доказательства, т. е. в качестве аксиом,— необходимо некоторое основание.

Таким основанием не может быть произвол, условное соглашение, субъективная точка зрения. Если в числе оснований данной науки имеются аксиомы, то в такой науке основанием для выбора системы или группы аксиом, входящих в начальные основания науки, являются следующие требования:

1. Выбранная группа аксиом должна представлять группу допущений, между которыми нет противоречий. Другими словами, группа аксиом должна быть такова, чтобы, опираясь на неё, нельзя было доказать суждение и отрицание этого суждения.

2. Выбранная группа аксиом должна быть такова, чтобы из неё (а также из принятых наукой определений) могла быть последовательно выведена вся совокупность теорем данной науки. При этом число аксиом не должно превышать того, какое необходимо и достаточно, чтобы с помощью данной группы аксиом могли быть доказаны все теоремы данной науки.

3. Ни одна из принятых в данной науке аксиом не может быть получена как вывод ни из какой другой аксиомы или других аксиом той же науки, т. е. каждая аксиома должна быть предположением вполне независимым от предположений, выражаемых всеми другими аксиомами данной науки.

Последнее свойство аксиом нуждается в объяснении. Свойство это нельзя понимать так, будто аксиома вообще не может быть выводима ни из каких других положений. Аксиома не может быть выводима из других аксиом только в рамках данной системы науки. Так, 11-я аксиома Евклида (постулат о параллельных) не может быть выведена из других аксиом геометрии Евклида. Именно поэтому все попытки доказать эту аксиому в рамках геометрии Евклида с её аксиомами и постулатами потерпели неудачу.

Но можно взять другую систему или группу аксиом геометрии. Можно выбрать такую группу аксиом, что постулат о параллельных, который в системе геометрии

Евклида является независимой аксиомой, будет в этой другой системе теоремой, выводимой из принятых в этой системе аксиом.

Таким образом, аксиоматическое значение некоторых положений науки не есть безусловное свойство этих положений. Разница между аксиомой и теоремой — не безусловная. Положение, которое в одной системе науки будет аксиомой, оказывается теоремой в системе науки с другой совокупностью аксиом. И наоборот: положение, доказываемое в данной системе науки как её теорема, не доказывается, а принимается в качестве аксиомы в системе науки с другой совокупностью аксиом.

В конечном счёте выбор той или другой группы аксиом (или постулатов) в качестве принятой в науке системы оснований её доказательств обусловливается и оправдывается не самоочевидностью этих оснований, а всей суммой результатов, к которым приводят доказательства науки, опирающиеся на принятые аксиомы и постулаты. Только содержательная плодотворность результатов, полученных с помощью принятой в данной системе науки группы аксиом, составляет основание для их выбора. Тем самым выбор оснований для всей системы доказательств науки — выбор аксиом или постулатов — связывается с проверкой этих оснований по их результатам, связывается с материальной практикой, с опытом.

Таким образом, с точки зрения современной логики, опирающейся на данные новейшей науки, аксиомами называются положения, не доказываемые в данной науке и играющие в ней — наряду с определениями основных понятий — роль допускаемых оснований всех доказываемых в науке истин. Роль эту аксиомы играют не в силу своей безусловной очевидности, хотя некоторые аксиомы представляются очевидными, и тем более не в силу своей априорности, так как никаких априорных положений нет ни в какой науке. Аксиомы данной науки выбираются в качестве аксиом. Однако основанием для выбора является не субъективный произвол, не «удобство», не «соглашение», а способность выбранной группы аксиом доказать всю совокупность известных истин науки, оправданных в своих результатах, т. е. в конечном счёте удостоверенных в своей истинности материальной практикой.

То, что в аксиомах не следует видеть истины безусловно недоказуемые, было не раз показано классиками марксизма-ленинизма. Энгельс говорит, что, например, аксиомы математики «доказуемы диалектически, поскольку они не чистые тавтологии»[21]. И точно также Ленин поясняет в конспекте «Науки логики» Гегеля, что фигуры силлогизма могли получить значение аксиом только после того, как значение это было доказано в миллиардах случаев опытом: «практическая деятельность человека миллиарды раз должна была приводить сознание человека к повторению разных логических фигур, дабы эти фигуры могли получить значение аксиом»[22].

Таким образом, и аксиомы как части оснований доказательства отнюдь не «возвышаются» над опытом, отнюдь не «предшествуют» опыту, а составляют результат материальной практики и опыта, лежащего в основе доказательства.

Все указанные выше требования, предъявляемые при выборе аксиом, имеют силу, разумеется, только в отношении тех наук, которые имеют в числе своих оснований аксиомы (постулаты) или, как говорят, допускают аксиоматическое построение. Таковы математика, теоретическая физика. Но существует обширный класс наук, в которых аксиоматическое построение неприменимо. В этих науках аксиомы (постулаты) не входят в число оснований науки» Такова, например, история.

г) Доказанные ранее положения науки как основания доказательства. Непосредственные и предшествующие основания доказательства. Начальные основания

В число оснований доказательств, кроме положений об удостоверенных фактах, на которые опирается доказываемый тезис, кроме определений основных понятий науки и аксиом, входят ещё доказанные ранее положения науки, необходимые для обоснования тезиса.

Так, при доказательстве теоремы евклидовой геометрии о сумме внутренних углов плоского треугольника в качестве оснований доказательства используют не только определения понятий, например понятий о параллельных, о смежных углах о внутренних накрест лежащих углах, о соответственных углах, и не только аксиомы, например аксиому (постулат) Евклида о параллельных. В качестве оснований доказательства этой теоремы используют также доказанную до неё теорему о равенстве суммы смежных углов двум прямым.

Рассматривая доказательство, нетрудно убедиться, что ранее доказанные положения, на которые опирается доказываемый тезис, используются в ходе доказательства либо непосредственным, либо опосредствованным образом.

Непосредственно используются те положения, на которые прямо ссылаются в ходе доказательства, как на положения, из истинности которых следует истинность доказываемого тезиса. Так, одним из положений, непосредственно используемых для доказательства теоремы Пифагора, будет 41-я теорема первой книги Евклида. Теорема эта утверждает, что если параллелограмм имеет с треугольником одно и то же основание и находится между теми же параллельными, то параллелограмм будет вдвое больше треугольника. Теорема эта принадлежит к непосредственным основаниям теоремы Пифагора, так как при доказательстве последней Евклид дважды ссылается в самом ходе доказательства на 41-ю теорему. Иными словами, 41-я теорема прямо входит в число оснований, истинность которых приводит к признанию истинности теоремы Пифагора.

Опосредствованным образом используются для доказательства те положения, на которые в самом ходе данного доказательства прямо не ссылаются, но при помощи которых были ранее доказаны непосредственные основания данного доказательства. Положения эти могут быть названы предшествующими основаниями доказательства. Так, для той же теоремы Пифагора одним из таких ранее доказанных, или предшествующих, оснований её доказательства будет 38-я теорема первой книги Евклида. Теорема эта утверждает, что треугольники, находящиеся на равных основаниях и между теми же параллельными, равны между собой. Эта теорема не входит в число непосредственных оснований доказательства теоремы Пифагора, так как в ходе этого доказательства Евклид на 38-ю теорему не ссылается. Но она входит в число оснований доказательства опосредствованным образом, будучи одним из оснований, при помощи которых была доказана 41-я теорема. А эта последняя есть, как мы уже знаем, одно из непосредственных оснований доказательства теоремы Пифагора.

Чем дальше развивает наука доказательства своих положений, тем большим становится число предшествующих оснований доказательства каждого нового положения. Если, рассматривая данный тезис науки, мы задались бы целью выяснить все основания, на которые опирается его доказательство, то оказалось бы, что непосредственные основания его доказательства опираются на некоторые предшествующие им основания, эти последние — в свою очередь на другие предшествующие основания и т. д. Однако, каким бы большим ни было число предшествующих оснований данного доказательства, оно не может быть бесконечным. Рано или поздно мы дойдём до таких предшествующих оснований, которые ни из каких предшествующих им оснований уже не могут быть выведены.

Основания доказательства, которые не могут быть выведены ни из каких предшествующих им оснований, называются начальными основаниями данной науки.

Начальными основаниями для данной науки являются: положения об удостоверенных единичных фактах, определения и аксиомы (постулаты). Теоремы не могут быть начальными основаниями, так как начальные основания ниоткуда не выводятся; напротив, всякая теорема — доказываемое положение, а все доказываемые положения выводятся из оснований непосредственных или предшествующих.

Все определения и аксиомы, которые могут встретиться в отдельных доказательствах в качестве непосредственных оснований или к которым доказательство может быть возведено как к своим предшествующим основаниям, входят в число начальных оснований науки. При этом, однако, в доказательства эти основания входят в каждом отдельном случае лишь частично. Так, доказательство, например, теоремы Пифагора опирается непосредственно не на все, а лишь на некоторые аксиомы, не на все, а лишь на некоторые определения, входящие в круг начальных аксиом и определений.

Напротив, в числе начальных оснований науки находится не часть аксиом, а все аксиомы данной науки, не часть определений, а все её определения.

Чем дальше отстоит доказываемое положение от начальных оснований данной науки, тем большим становится число предшествующих оснований доказательства. И действительно: каждое доказанное ранее положение, на которое в данном доказательстве наука ссылается, как на одно из непосредственных оснований доказываемого тезиса, обусловлено, в свою очередь, длинным рядом предшествующих ему положений. Ни на одно из них в пределах данного доказательства не ссылаются — иначе доказательство каждой теоремы было бы повторением всего предшествующего этой теореме содержания науки со всеми её доказательствами. В то же время все они могут быть найдены в соответствующем месте системы науки, где они полностью излагаются, иначе основание, на которое опирается доказываемое положение, само было бы -недоказанным.

Наличие в далеко продвинувшейся науке длинной цепи не непосредственных оснований, предполагаемых каждым непосредственным основанием любого доказательства, делает особенно важным условием состоятельности доказательства истинность всех оснований доказываемого тезиса.

В самом деле, непосредственное для данного доказательства основание есть только звено предшествующей ему цепи обусловливающих его оснований. Если эта цепь длинна и если какое-нибудь из её звеньев окажется ложным, то и заключительное звено — данное непосредственное основание доказательства — тоже может оказаться ложным. А в таком случае и доказываемый тезис, как опирающийся на ложное основание, может оказаться ложным.

Поэтому в качестве оснований доказательства должны быть принимаемы только истинные, строго доказанные, проверенные и удостоверенные в своей истинности положения. Любой вид оснований, вообще говоря, сказывается на истинности результата. Поэтому ни входящие в число оснований доказательства положения об удостоверенных фактах, ни определения основных понятий науки, ни аксиомы, ни уже ранее доказанные положения науки не должны быть ложными. Основания доказательства не должны быть даже сомнительными. Сомнительность основания есть по крайней мере возможность его ложности, а возможность ложности в основаниях доказательства делает возможным ложность самого доказываемого тезиса. Поэтому доказательство, опирающееся на сомнительные основания, не есть, строго говоря, подлинное доказательство. Только вполне удостоверенная истинность всех оснований, на которые опирается доказательство, делает доказательство (при соблюдении всех прочих условий и правил, о которых речь впереди) путём и средством к отысканию новой истины.