3.5. Логическое следование

3.5. Логическое следование

Основная задача логики состоит в том, чтобы исследовать, какие следствия вытекают из данных утверждений, например, какие теоремы в математике следуют из принятой системы аксиом. Интуитивно мы можем выводить заключения, не обращаясь к логической символике и технике и даже ясно не сознавая те логические правила, которыми неявно пользуемся. Однако в более трудных случаях интуитивных возможностей оказывается недостаточно, в особенности когда приходится проверять рассуждения и анализировать ошибки. Даже в простейших случаях можно допустить ошибку, как показывает следующий пример.

"Если не будет дождя (¬Д), то он придет на встречу (В)". Пошел дождь, значит он не придет на встречу (¬В). Переведем эту словесную формулировку на логический язык исчисления высказываний и тогда получим формулу:

((¬Д ? В) ? Д)) ? ¬В (1)

Чтобы проверить правильность заключения, построим для него таблицу истинности (табл. 8).

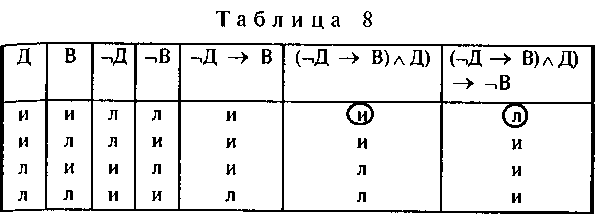
Хотя заключение словесного рассуждения кажется на первый взгляд верным, но оно логически не следует из посылок, в чем можно убедиться, если сравнить значение истинности посылок формулы (1) со значением истинности заключения. Если бы заключение логически следовало из посылок, тогда при одновременной истинности посылок (¬Д ? В) в первой строке табл. 8 и Д заключение ¬В в последнем столбце этой же строки должно быть истинным, а оно ложно. Но фундаментальный принцип логики постулирует, что из истинных посылок нельзя вывести ложного заключения. Это и показывает, что рассматриваемое заключение не следует из посылок. Ведь не исключается возможность, что несмотря на дождь, человек может прийти на встречу.

Отсюда становится ясным, что установить логическое следование одного высказывания или формулы из другого можно с помощью построения таблицы истинности всех входящих в формулы простых (элементарных) высказываний, которые называют атомарными (или просто атомами). В противоположность этому сложные (составные) высказывания, построенные с помощью логических связок, рассматривают как молекулярные. Если будет установлено, что при одновременной истинности посылок заключение окажется также истинным, то это дает основание сказать, что данная формула или высказывание логически следует из другой или других, т.е. заключение следует из посылок. В противном случае, как мы видели в предыдущем примере, заключение логически не следует из посылок.

Теперь дадим общее определение логическому следованию в исчислении высказываний. Обозначим через заглавные буквы латинского алфавита молекулярные высказывания А и В, состоящие из атомарных (элементарных) высказываний х₁ , х₂ , x₃ ,..., x_n. Тогда говорят, что "В следует из А или является следствием А", когда в таблицах истинности для А и В формула В имеет значение "истина" во всех тех строках, где А имеет значение "истина". Символически следование обозначается знаком " | =", например А | = В.

Если из А логически следует В, а из В следует А, т.е. А | = В и В | =А, то в этом случае высказывания А и В будут логически эквивалентными.

Обратимся теперь к другому случаю и определим, например, следует ли формула х ? у из формулы (х ? у) ? (x ?¬ y). Для этого снова построим таблицу их истинности (табл. 9).

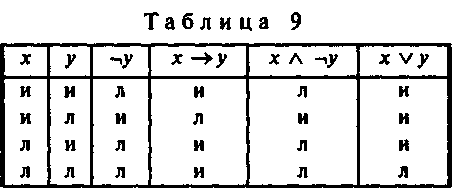
Однако в этой таблице ни в одной строке высказывания х ? у и х ? ¬у не являются одновременно истинными, а потому их конъюнкция будет ложной. Но импликация из ложного высказывания считается истинной. Можно сказать поэтому, что из рассматриваемой формулы следует не только дизъюнкция х v у, но и любая другая формула. Такой парадоксальный результат объяснить нетрудно. Дело в том, что формула (х ? у) ? (х ? ¬у) представляет собой логическое противоречие, в чем можно убедиться, если выразить ее вторую часть через импликацию, т.е. (х ? ¬у) ¬( ? x ? y). Отсюда непосредственно видно, что второй член конъюнкции является отрицанием первого члена: (х ? у) ? ¬(х ? ¬у).

Такого рода высказывания, в котором одно из них что-то утверждает, а другое одновременно отрицает это, называются контрадикторными (противоречащими). Согласно известному нам закону непротиворечия подобные высказывания недопустимы в рассуждении, ибо из логически противоречивого утверждения следует любое высказывание: истинное или ложное.

Часто противоречивые высказывания называют также несовместными, потому что из несовместных высказываний логически следует противоречие.

Несовместность (противоречивость) высказываний, которая иногда встречается в рассуждениях, приводит к тому, что в нем оказываются допустимыми как истинные, так и ложные заключения. Именно этим обстоятельством широко пользовались античные софисты, стремившиеся обеспечить себе победу в споре любой ценой, в том числе и путем нарушения законов логики. Очевидно, что для этого они маскировали свои утверждения, ибо в противном случае оппоненты и слушатели всегда могли изобличить их в явных противоречиях. Однако никто не застрахован от противоречий и ошибок, но следует различать ошибки преднамеренные (сознательные) и ошибки не преднамеренные (неосознаваемые). Если первые, которые часто называют софизмами, следует разоблачать, то вторые, именуемые паралогизмами, необходимо исправлять. Но в обоих случаях логика служит надежным инструментом для анализа и раскрытия ошибок, и в особенности определения правильности логического следования заключения из его посылок.

В первом примере ошибочное заключение было связано с недостаточной точностью его словесной формулировки, во втором примере - противоречие было замаскировано другой формой символической записи второй части формулы. Ясно, что если бы противоречие было записано в виде: (х ? у) и ¬(x ? у), то сразу стало бы видно, что здесь перед нами противоречие, из которого, как теперь мы знаем, следует любое заключение: истинное, ложное и даже абсурдное. Нельзя, однако, считать, что противоречия раскрываются так легко. Как будет показано в гл. 6, противоречия зависят от ряда условий, выполнение которых обязательно для того, чтобы характеризовать их как противоречия, в частности чтобы высказывания, из которых одно отрицает другое, характеризовали предмет мысли в одно и то же время и в одном и том же отношении. С течением времени наши знания изменяются, и поэтому высказывания, которые характеризовали явления, также могут измениться и перестать противоречить друг другу.

Легко заметить, что все рассмотренные выше контрадикторные (противоречащие) высказывания могут быть представлены с помощью общей формулы (А ? ¬А), где члены конъюнкции А и ¬А являются выражениями метаязыка, т.е. языка, на котором мы говорим об объектном (предметном) языке. Метаязык служит для представления высказываний, которые выражаются с помощью переменных х₁ , х₂ , x₃ ,..., x_n. В дальнейшем формулы метаязыка будут применяться всякий раз, когда нам придется говорить о предметном языке, чтобы не загромождать изложение и не выписывать формулы этого языка.

Итак, любые сколь угодно сложные высказывания, которые могут быть представлены в форме конъюнкции утверждения и его отрицания, т.е. как А ? ¬А, представляют именно противоречие. Поэтому при любой комбинации входящих в них высказываний по истинностному их значению ("истина" или "ложь") будут приводить к ложному заключению. Другими словами, функция-высказывание, образованное из элементарных высказываний, всегда будет иметь своим значением "ложь". Поскольку из ложного утверждения можно получить как истину, так и ложь, постольку основной закон логики - закон непротиворечия - запрещает использовать противоречивые высказывания или формулы в рассуждении. Этот запрет выражается в требовании непротиворечивости рассуждения, которую часто называют также требованием совместимости (связности) рассуждения.

Если формула (А ? ¬А) является всегда ложным высказыванием, то ее отрицание, выражающее требование непротиворечивости, напротив, будет всегда истинным высказыванием, общезначимой формулой, или тавтологией, как стали называть такие высказывания вслед за Л. Витгенштейном. Следует, однако, не смешивать языковые тавтологии с логическими. Если в языке тавтология означает повторение той же фразы или предложения текста, то в логике она является тождественно истинным высказыванием. Не следует также путать тождественно истинные высказывания с законом тождества, который выражается формулой А ? А, хотя последняя также выражает тавтологию.

Отсюда становится ясным, что тавтологии (тождественно истинные высказывания) можно использовать для представления всех законов логики или любых общезначимых ее формул. Действительно, закон непротиворечия, запрещающий противоречия в рассуждении, можно выразить формулой ¬(A ? ¬A), которая представляет собой тавтологию, в чем можно убедиться, построив для нее соответствующую таблицу истинности (табл. 10). То же самое можно сказать о законе исключенного третьего - (A ? ¬A) (табл.11).

Если из противоречия следует все, что угодно, т.е. "истина" или "ложь", то и тавтология следует из любого истинного или ложного высказывания. В самом деле, если в каждой строке таблицы заключение всегда будет истинным, то по правилу импликации оно может быть получено как из истинных, так и из ложных посылок. Напротив, никогда ложное следствие (противоречие) не может быть получено из истинных посылок.

Промежуточное положение между всегда истинными высказываниями (тавтологиями), с одной стороны, и всегда ложными (противоречивыми) высказываниями, с другой, занимают фактуальные утверждения. Их заключения могут быть как истинными, так и ложными, в зависимости от тех фактов, на которые опираются их посылки. В то время как истинность тавтологий или ложность противоречий может быть установлена чисто логическим анализом этих высказываний, значение истинности фактуальных высказываний требует обращения к действительным фактам. Другими словами, чтобы установить истинность или ложность фактуальных высказываний, необходимо исследовать реальные связи и отношения действительности, которые отображаются в соответствующих высказываниях, служащих посылками фактуальных заключений. На этом основании фактуальные высказывания часто называют также эмпирическими в противоположность аналитическим высказываниям логики и чистой математики. Но это противопоставление имеет относительный характер, ибо и в научных, и в повседневных рассуждениях аналитические высказывания логики применяются вместе с эмпирическими утверждениями, поскольку именно из эмпирических законов мы выводим логические заключения.

Всю новую информацию в науке формулируют с помощью эмпирических (фактуальных) высказываний, а выводы из нее получают с помощью законов (правил) логического следования.