Геометрия

Геометрия

Чтобы понимать пространство, давайте рассмотрим геометрию – структуру пространства. К счастью, большинство людей понимают геометрию легче, чем алгебру. Геометрия образна; она имеет художественную форму и кажется менее абстрактной, чем формулы алгебры. Например, возьмем алгебраическую формулу c² = а² + Ъ² – формулу Пифагора для самой длинной стороны, или гипотенузы, прямоугольного треугольника. Большинству из нас эта формула, вероятно, кажется более сложной, чем ее геометрический эквивалент, изображение прямоугольного треугольника.

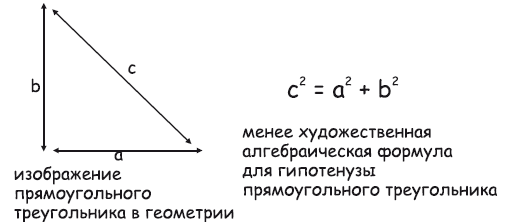
Рис. 26.1 Сравнение геометрии и алгебры

На рисунке 26.1 формула описывается с помощью чертежа. Чертеж дает графическое объяснение формулы. Формула гласит, что для нахождения расстояния между точками 1 и 2, следует найти расстояния а и b, возвести их в квадрат, сложить квадраты и извлечь квадратный корень из суммы. Поскольку геометрия представляет собой карту, она играет центральную роль в описании не только физической Вселенной, но и духовной Вселенной в религии и психической сферы цельности в психологии.

Например, одна из центральных духовных и психологических формул, или геометрических структур, стоящих за нашим поведением, в различных религиозных традициях и в психологии Юнга изображается в виде круга или мандалы – симметричной фигуры из Индии. Юнг считал, что мандала символизирует цель человеческого поведения – цельность или индивидуацию, как он ее называл. Мандала подразумевает, что мы имеем много сторон и должны развивать их в равной мере. Мандалы имеют много форм; они могут быть круглыми или квадратными, звездообразными или продолговатыми, но они всегда симметричны.

Имея симметричный шар, вы можете вращать его в любых направлениях, и его форма не меняется. Квадраты менее симметричны, чем круги. Вы может поворачивать круг или сферу как угодно, и они остаются теми же самими. Чтобы квадрат оставался одним и тем же, вы должны каждый раз поворачивать его точно на четверть оборота. Прямоугольники еще менее симметричны; чтобы они оставались одними и теми же, их приходится поворачивать на 180 градусов. Это справедливо и для крестов; если его перекладина выше основания, то крест симметричен при вращении справа налево или слева направо; при таком вращении его форма остается той же самой. Однако форма меняется, если вы переворачиваете его кверху ногами. Шестиконечная звезда симметрична при повороте на 60 градусов; для пятиконечной звезды угол поворота должен быть немного больше.

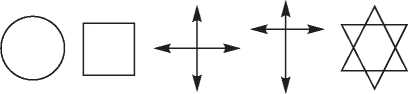
Рис. 26.2. Примеры симметричных объектов

В геометрии есть много симметричных структур, которые иллюстрируют нашу глубинную склонность становиться завершенными, цельными существами. Симметрии имеют фундаментальное значение и для законов физики. Немного дальше мы вместе исследуем происхождение этих симметрий.