§ 39. Геометрия

§ 39. Геометрия

Так же на связи положения частей пространства основана вся геометрия. Поэтому она должна была бы быть разумением этой связи; но так как оно, как сказано выше, посредством понятий невозможно, а дается только созерцанием, то каждый геометрический закон должен был бы сводиться к такому созерцанию, и доказательство заключалось бы в ясном выявлении связи, от созерцания которой все зависит; ничего больше нельзя было бы сделать. Между тем мы видим, что в геометрии действуют совершенно иные методы. Только двенадцать аксиом Евклида считают основанными на созерцании, и даже из них только девятая, одиннадцатая и девятая основаны на отдельных различных созерцаниях, все же остальные — на понимании того, что в науке мы имеем дело, не как в опыте, с реальными вещами, которые пребывают сами по себе друг подле друга и могут быть до бесконечности различными, а с понятиями,— в математике с нормальными созерцаниями, т. е. с фигурами и числами, служащими законом для всякого опыта и поэтому соединяющими многообъемлемость понятия с полной определенностью единичного представления. Ибо хотя они в качестве созерцаемых представлений полностью определены и таким образом не оставляют места для общности, обусловленной неопределенностью, они тем не менее всеобщи, ибо суть только формы всех явлений и в качестве таковых применимы ко всем объектам, которым присуща подобная форма. Поэтому даже в геометрии к этим нормальным созерцаниям, как и к понятиям, можно применить то, что Платон говорит об идеях: что не могут существовать две одинаковые идеи, так как они были бы одной*. Это было бы, говорю я, применимо и к нормальным созерцаниям в геометрии, если бы они в качестве только пространственных объектов не различались пребыванием друг подле друга, местом. Это, по словам Аристотеля, заметил и сам Платон: item praeter sensibilia et species, mathematica rerum ait media

esse, a sensibilibus quidem differentia eo, quod perpetua et inmobilia sunt, a speciebus vero eo, quod illorum quidam multa, quaedam similia sunt, species vero ipsa unaquaeque sola⁰⁸⁵ (Metaph. 1, 6, с этим следует сравнить X, 1). Понимание того, что подобное различие в месте не уничтожает тождества в остальном, могло бы, Как мне кажется, заменить те девять аксиом и более соответствовало бы сущности науки, цель которой познавать единичное из общего, чем построение девяти различных аксиом, основанных на одном соображении. Тогда к геометрическим фигурам относились бы слова Аристотеля: in illis aequalitas unitas est (Metaph. X, 3).

*Платоновские идеи можно описать как нормальные созерцания, применимые не только, подобно математическим, к формальному, но и к материальному в полных представлениях; следовательно, как полные представления, которые в качестве таковых вполне определенны и вместе с тем, как понятия, охватывают многое, т. е. согласно моему объяснению в § 28 служат представителями понятий, им, однако, совершенно адекватных.

Что же касается нормальных созерцаний во времени, чисел, то для них нет даже различия в пребывании друг подле друга, а есть просто, как в понятиях, identitas indiscernibilium⁰⁸⁶ и существует только одно пять и только одно семь. И здесь можно было бы найти основание того, что 7 + 5 = 12 не идентичное, как утверждает Гердер в своей «Метакритике», а, как глубокомысленно определил Кант, синтетическое суждение a priori, основанное на чистом созерцании. Идентичное суждение — это 12 = 12.

Следовательно, на созерцание в геометрии ссылаются, собственно, только в аксиомах. Все остальные теоремы доказываются, т. е. приводится такое основание познания теоремы, которое заставляет каждого признать ее правильной: следовательно, выявляют логическую, а не «трансцендентальную истинность теоремы (§§ 30 и 32). Истинность, которая лежит в основе бытия, а не познания, становится Очевидной только посредством созерцания. Поэтому после проведения геометрического доказательства мы обретаем, правда, уверенность в том, что доказанная теорема истинна, но совсем не понимаем, почему то, что она утверждает, таково, как оно есть, т. е. не проникаем в основание бытия, более того, обычно только теперь у нас возникает потребность в нем. Ибо доказательство посредством: указания на основание познания действует только как убеждение (convictio), не как уразумение (cognitio), поэтому было бы, пожалуй, вернее называть его elenchus, а не demonstratio⁰⁸⁷ . Этим объясняется, что оно оставляет обычно неприятное чувство, которое мы всегда испытываем при неполноте знания, причем здесь недостаточное знание того, почему нечто так, становится ощутимым посредством: данной уверенности в том, что это так. Ощущение при этом похоже на то, что мы испытываем, когда у нас незаметно вынимают что–либо из кармана или кладут туда, и мы не понимаем, как это было сделано. Данное основание познания без основания бытия, как это происходит в подобных демонстрациях, аналогично ряду физических положений, которые показывают явление, не умея объяснить его причину, как, например, опыт Лейденфроста, поскольку он удается в платиновом тигле. Напротив, познанное посредством созерцания основание бытия геометрической теоремы дает удовлетворение, как каждое обретенное знание. Если мы постигли основание бытия, то уверенность в истине теоремы зиждется только на нем, а отнюдь не на основании познания, данном доказательством. Например, шестую теорему своей первой книги: «Если в треугольнике два угла равны, то равны и противоположные им стороны» — Евклид доказывает так (см. рис. 3): в треугольнике abg угол abg равен углу agb; я утверждаю, что тогда и сторона ag равна стороне ab.

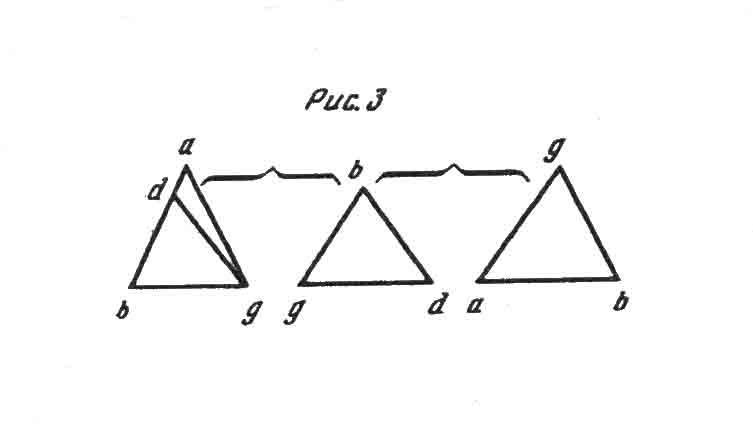
Ибо если сторона ag не равна стороне ab, то одна из них больше другой. Отнимем от большей стороны ab отрезок db, равный меньшей линии ag, и проведем линию dg. Так как (в треугольниках dbg, abg) db равна ag, a bg принадлежит обеим, то две стороны db и bg равны двум сторонам ag и gb, взятым в отдельности, угод dbg равен углу agb, основная линия dg равна основной линии: ab, и треугольник abg равен треугольнику dbg, больший меньшему, что бессмысленно, следовательно, ab не неравна ag, следовательно, равна.

В этом доказательстве мы имеем основание познания истинности: теоремы. Но кто же основывает свою уверенность в этой геометрической истине на подобном доказательстве, а не на познанном созерцанием основании бытия, по которому (в силу необходимости, не допускающей дальнейшего доказательства, а доступной только созерцанию), если из обоих конечных точек линии исходят две другие линии и равномерно наклоняются друг к другу, они могут встретиться только в одной точке, находящейся на одинаковом: расстоянии от обеих конечных точек, потому что два возникающих угла составляют, собственно, только один угол, кажущийся двумя углами только из–за противоположного положения; поэтому нет основания, чтобы линии встретились ближе к одной точке, чем к другой.

Познавая основание бытия, мы выводим как необходимое следствие, обусловленное его условием, в данном случае — равенство сторон из равенства углов,— их связь; основание же познания дает нам только совместное бытие обоих. Более того, можно даже утверждать, что обычный метод доказательства убеждает нас, собственно, лишь в том, что оба равенства выступают в данной, принятой в доказательстве фигуре, а отнюдь не в том, что они всегда выступают вместе; в этой истине (поскольку необходимая связь не показана) мы обретаем только уверенность, основанную на индукции, и покоится наше убеждение на том, что это обнаруживается в каждой фигуре, построенной нами. Правда, столь легко основание бытия бросается в глаза только в таких простых теоремах, как шестая теорема Евклида; однако я убежден, что в каждой, даже самой запутанной, теореме его можно выявить и свести достоверность теоремы к такому простому созерцанию. К тому же каждый a priori сознает необходимость такого основания бытия для каждого пространственного отношения, подобно необходимости причины для каждого изменения. Конечно, обнаружить такое основание в сложных теоремах очень трудно, а здесь не место проводить сложные геометрические исследования. Поэтому только для того, чтобы еще больше уяснить свою мысль, я сведу к основанию бытия не очень сложную теорему, в которой, однако, это основание не сразу бросается в глаза.

Пропускаю десять теорем и перехожу к шестнадцатой: «В каждом треугольнике, одна сторона которого продолжена, внешний угол больше, чем каждый из двух противостоящих ему внутренних». Доказательство Евклида таково (см. рис. 4).

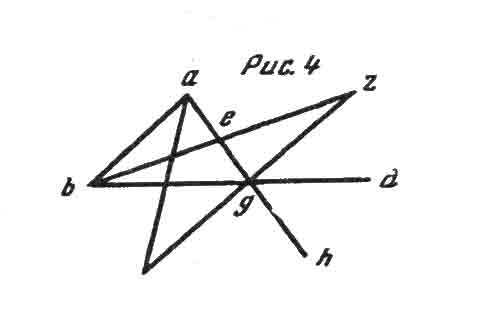
Возьмем треугольник abg, продолжим сторону bg к d, и я утверждаю, что внешний угол agd больше, чем каждый из двух противостоящих ему внутренних. Разделим сторону ag пополам в точке е, проведем линию be, продолжим ее до z p сделаем ez равной еb, соединим точки z и g и продолжим ag до h. Так как ае равна eg и be равна ez, то две стороны ае и eb равны двум сторонам ge и ez, взятым в отдельности, и угол aeb равен углу zeg, ибо это — вертикальные углы. Тем самым основная линия ab равна основной линии zg и треугольник аbe равен треугольнику zeg: а остальные углы равны остальным углам, следовательно, и угол bae равен углу egz. Однако угол egd больше угла egz, следовательно, и угол agd больше угла bae. Если разделить пополам и линию bg, то подобным же образом можно доказать, что угол bgh, т. е. его вертикальный угол agd, больше, чем abg.

Я бы доказал эту теорему следующим образом (см. рис. 5). Для того чтобы угол bag был равен, а тем более превзошел бы, угол agd, линия ba (ибо это и означает равенство углов) должна была бы находиться по отношению к линии ga в том же направлении, как bd, т. е. быть параллельной bd, другими словами, никогда не пересекаться с bd; однако для того чтобы образовать треугольник, она должна (основание бытия) пересечься с bd, т. е. совершить противоположное требуемому для того, чтобы угол bag хотя бы достиг величины угла agd.

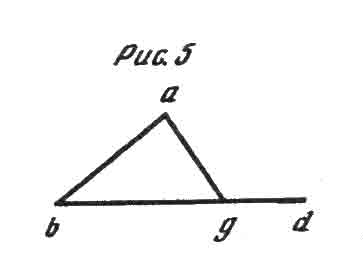
Для того чтобы угол abd был равен углу agd, а тем более превосходил его (ибо именно это и означает равенство углов), линия bа должна была бы находиться по отношению к линии ga в том же направлении, что bd, т. е. идти параллельно bd, другими словами, никогда не пересекаться с ней; но для того чтобы образовать треугольник (основание бытия), она должна пересечься с линией ag, следовательно, совершить противоположное требуемому для того, чтобы угол abg хотя бы достиг величины угла agd.

Всем этим я отнюдь не хотел предложить новый метод математических демонстраций или заменить моим доказательством доказательство Евклида; для этого оно не подходит по всему своему характеру, а также потому, что оно предполагает понятие параллельных линий, которое лишь позже встречается у Евклида; я хотел лишь показать, чт? есть основание бытия и чем оно отличается от основания познания, которое действует лишь convictio, а это нечто совсем другое, чем понимание основания бытия. То, что в геометрии стремятся действовать лишь convictio, что производит неприятное впечатление, а не пониманием основания бытия, которое, как всякое понимание, удовлетворяет и радует, послужило, вероятно, одной из причин того, что многие люди глубокого ума не склонны заниматься математикой.

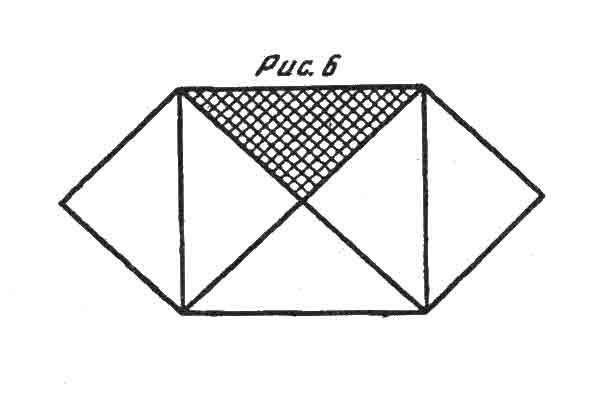
Не могу удержаться, чтобы не поместить здесь еще раз уже данную в другом месте фигуру (рис. 6); один взгляд на нее, без всяких рассуждений, убеждает в истинности теоремы Пифагора в двадцать раз больше, чем запутанное доказательство Евклида. Читатель, которого заинтересовала эта глава, найдет дальнейшее рассмотрение этой темы в «Мире как воле и представлении», т. 1, § 15 и т. 2, гл. 13.