Евклидова и неевклидова геометрия

Евклидова и неевклидова геометрия

К 1900 г. большинство математиков и физиков уже утратили контакт со священными силами, стоящими за математикой, или с математикой, которая представляет собой описание Вселенной, отражающей саму себя. По существу, пространства физики были очень похожи на квадратные комнаты нашей общепринятой реальности. Центральное место в науке занимало дедуктивное рассуждение древних греков. Боги и богини временно маргинализировались.

Самым распространенным представлением о пространстве среди физиков в 1900 г. было то, что математики называют «пространством-два» или «плоской страной», поскольку его можно представлять себе в виде лежащего на столе листа бумаги с нарисованными на нем кругами и квадратами. Мир физики был евклидовым и предполагался состоящим из кругов и треугольников, поддающихся измерению с помощью теорем, которые многие из нас учили в школе.

Землемеры в Вавилоне и Древней Греции использовали формулы квадратов и треугольников для измерения площади своей собственности. Конечно, чтобы наносить на карту расстояние от одного города до другого, они могли проходить это расстояние пешком. Но им было трудно измерить расстояние, если в середине него был крутой холм. Формулы дают обобщения, которые помогают вам, когда вы не можете двигаться по прямой линии, чтобы измерить расстояние. Чтобы измерить расстояние, которое могла бы пролететь птица между вашим городом A и соседним городом C, можно просто использовать формулу для прямоугольного треугольника.

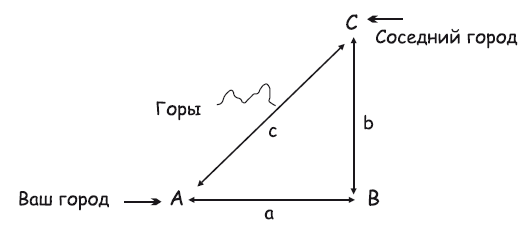
Рис. 26.6. Измерение расстояния между A и C

Если между A и C находятся горы (рис. 26.6), то для того, чтобы найти расстояние с, вам нужно только знать сумму a² и b² (при условии, что там нет гор). Вам не нужно непосредственно измерять расстояние между A и C. Геометрические формулы говорят вам, как далеко друг от друга в пространстве находятся разные места, даже когда вы не можете непосредственно измерить расстояние между ними.

Оказывается, что при измерении больших расстояний, например между планетами в пространстве, мы не можем использовать эту формулу Евклида или, вернее, Пифагора для треугольников. В действительности, больше не пригодны формулы для расстояний, треугольников, квадратов и кругов. Нам нужна новая формула – формула неевклидовой геометрии, которая имеет дело с кривыми.

Чтобы понять некоторые особенности, связанные с криволинейным мышлением, мы можем начать с использования более или менее сферической Земли, на которой мы живем. Если вы путешествуете на самолете вокруг света и летите вдоль экватора, то, в конце концов, попадете туда, откуда вы начинали свой полет, поскольку мы живем на поверхности сферы.

Самый быстрый путь по воздуху между двумя точками на Земле представляет собой не прямую, а кривую линию. Добираясь из Портленда, штат Орегон, в Париж, вы экономите около тысячи миль, если летите низко над землей, но вы не летите в Париж по прямой. Вместо этого, вы сперва должны двигаться на север, а не на восток.

Чтобы составить себе представление о путешествии в пустом пространстве, давайте рассмотрим полет в космос. Если вы начинаете оттуда, где вы находитесь, скажем из Портленда, и не двигаетесь вокруг планеты, а оставляете Землю и направляетесь прямо в космос, то, в конце концов, вернетесь в Портленд! Почему? Потому что, согласно нашим самым современным теориям, пространство криволинейно и Вселенная замкнута.

Еще один способ зрительного представления кривизны пространства состоит в измерении прямизны пути автоматной очереди или ее квантового эквивалента – луча фотонов между двумя точками. Если бы не было тяготения и сопротивления воздуха, вы бы ожидали, что пули или фотоны движутся по прямой линии. Но наши ожидания оказываются неверными. Мы едва ли замечаем, что ошибаемся, пока остаемся на Земле, но даже хотя мы этого не замечаем, путь фотонов является не прямым, а искривленным.

Кривизна так мала, что до начала 1900-х гг. ее никто не замечал. Эйнштейн показал, что пространство искривлено, и у него даже была физическая догадка, почему это так. Он утверждал, что путь пучка фотонов искривляет количество материи в его окрестностях. Разумеется, пучок фотонов – это свет. Другой способ формулировать ту же самую мысль состоит в том, что изгибается не луч света, а само пространство. С этой точки зрения, материя или тяготение изгибает пространство. Поэтому все, что должно двигаться по прямой в гипотетическом евклидовом мире, не может этого делать во Вселенной, где мы живем, поскольку ее пространство изогнуто.

Со времени открытия относительности нам приходится представлять себе пространство как субстанцию, как материал, который изгибается и искривляется в зависимости от того, сколько рядом материи. Если вы находитесь вблизи большой планеты, то пространство изогнуто сильно. На Земле пространство изогнуто не слишком сильно. Таков, вкратце, результат общей теории относительности. Мы продолжим изучение этой области в нескольких следующих главах.

Специальная теория относительности, которую мы обсуждали ранее, имеет дело с относительными системами отсчета, которые движутся относительно друг друга в пространстве-времени более или менее прямолинейно и равномерно. Общая теория имеет дело с системами, которые движутся не с постоянными, а с меняющимися скоростями – замедляясь и ускоряясь.

В то время как специальную теория относительности сегодня признают большинство физиков, общая теория математически сложна и до сих пор продолжает исследоваться. Но сама идея, что пространство искривлено и что кривизна связана с количеством присутствующей материи, стала вполне общепризнанной среди теоретиков.

Идея пространства уже кажется странной некоторым людям, но что если мы затем добавляем изогнутое пространство? Это поистине непонятно. Идея о том, что материя искривляет пространство, невероятна, и ее мог придумать только кто-то вроде Эйнштейна. Он понимал, что если мы живем во Вселенной, где свет изгибается, и если правда, что пространство не является прямолинейным и плоским, значит, не существует никаких правильных треугольников или кругов. В нашей Вселенной треугольники и круги искривлены и их нельзя точно нарисовать на плоском листе бумаги. Более того, идеи и формулы евклидовой геометрии, которые многие из нас учили в школе, верны только для вашего непосредственного окружения. Для Вселенной нам нужна геометрия, которая работает с кривыми.

Данный текст является ознакомительным фрагментом.