Проблемы методологии системного исследования[73]

Проблемы методологии системного исследования[73]

Системы и структуры как проблема современной науки и техники

Развитие современной науки характеризуется не только необычайно быстрым накоплением все новых и новых знаний, но и тем, что существенно изменились и продолжают меняться принципы и методы научно-исследовательской работы. Среди понятий, наиболее концентрированно выражающих этот процесс, исключительное место принадлежит понятиям системы и структуры. Внешне это проявляется прежде всего в том, что термины, обозначающие их, стали сейчас самыми распространенными в научной и популярной литературе. Лингвист не может написать нескольких предложений, не упомянув о системе языка, химик — о структурах соединений, кибернетик — о системах управления, логик — о системе знаний, биолог — о структурности организма, и все они употребляют эти слова, как говорится, «с большой буквы», вкладывая в них особый, веский смысл.

И дело здесь не просто в моде. Изучение объектов как структур и систем стало в настоящее время основной задачей по сути дела всех наук. Эта направленность в способах понимания или, можно сказать, «виденья» объектов начала формироваться уже давно, но только во второй четверти XX столетия произошел действительно переворот во взглядах и она получила повсеместное распространение и признание.

Победа новой точки зрения и широкий переход к системным предметам и проблемам были обусловлены не только внутренним развитием самих наук, но во многом также развитием современного производства. Характерное и знаменательное явление наших дней — технические системы «большого масштаба», нередко комплексно автоматизированные и обслуживаемые сложнейшими электронно-вычислительными машинами. Рациональное управление экономикой в целом и отдельными ее отраслями, даже отдельными предприятиями требует целостного представления о системе, включающей в себя производство и его организацию, сложную сеть коммуникаций различного рода, организацию снабжения и сбыта и т. п. С системами гигантского масштаба, охватывающими целую страну и даже несколько стран, сталкиваемся мы и в военном деле. Чтобы управлять подобными системами, их нужно специально изучать. Так развитие производства и техники влияет на формирование новых системных предметов и проблем исследования.

Но значение этих проблем не только в том, что к ним обращаются в разных и многих научных дисциплинах. Значительно важнее, что в решении их заключен, по-видимому, какой-то узел развития науки в целом, ее «технологии», т. е. приемов и способов самого исследования. Для лингвиста в первую очередь важно выяснить, конечно, что представляют собой системы языка, для биолога — что представляет собой то или иное живое целое или популяция, для социолога — определенная социальная система. Но для науки в целом значительно важнее другое — постараться нащупать какие-то пути и способы, которые вообще сделали бы возможным исследование объектов как систем и структур. Ибо нынешние достижения человечества в решении этих проблем, несмотря на все их практическое и теоретическое значение, еще очень и очень незначительны.

Известный австрийский биолог Л. Берталанфи, живущий сейчас в Канаде, создал специальное общество для разработки «общей теории систем». Оно объединяет многих ученых самых различных специальностей, которые от частных проблем отдельных специальных наук пришли к постановке общих методологических вопросов [Лекторский, Садовский, 1960]. Этот факт — признание необходимости общего подхода к анализу систем и структур. Но вместе с тем приходится признать, что именно общих решений пока нет, и это отрицательно сказывается на развитии специальных наук. Приемы и способы системного и структурного исследования остаются пока еще не разработанными фактически во всей науке, и поэтому так важно и полезно сейчас встать на более широкую точку зрения, постараться выяснить не только то, каковы системы языка, живого организма, социального или экономического целого, но и то, как мы их исследуем, как вообще их можно исследовать.

Иными словами, это можно сказать так: именно из-за того, что в исследовании объектов как систем и структур мы сталкиваемся сегодня со значительными трудностями и природа этих трудностей оказывается в принципе одинаковой в разных областях, необходимо всемерно развертывать специальные логико-методологические исследования. Их задача состоит в том, чтобы сформулировать систему общих принципов и правил, в соответствии с которыми можно было бы строить системно-структурное исследование частных объектов.

В условиях современной науки методологический анализ вообще приобрел первостепенное значение, поскольку исследователь имеет дело, как правило, с исключительно сложными познавательными конструкциями, выступающими в качестве средств анализа. Именно этим следует объяснить повсеместное резкое усиление внимания к методологическим проблемам науки. Им было посвящено, как известно, и специальное расширенное заседание президиума Академии наук СССР в октябре 1963 г. [Методологические… 1964]. В выступлениях ведущих советских ученых было показано, что специальный методологический анализ стал органически необходимым в решении по сути дела всех фундаментальных задач современной науки.

Так мы естественно приходим к необходимости более подробно и детально обсудить вопрос о том,

в чем специфика методологического подхода к проблемам науки.

Задача представителя специальной науки состоит в том, чтобы построить знание о предмете своего изучения, или, иначе, описать этот предмет в некоторой знаковой форме. При этом ученый пользуется средствами и методами, уже выработанными в его науке. Пока они «работают» безотказно и дают знания, хорошо согласующиеся между собой и отвечающие поставленным задачам, ему не приходится задумываться по поводу их характера и строения. Иное положение складывается, когда встают задачи, не разрешимые старыми средствами и методами, или когда появляются новые объекты, к которым старые средства не могут быть приложены; тогда условием решения задачи становится создание новых средств и методов.

Как это делается? Возможны две полярные линии. Одна — это путь «искусства».[74] Он заключается в комбинировании уже существующих в данной науке средств и методов, в многочисленных пробах, приводящих в конце концов к трансформации этих средств и к нахождению случайного решения, в попытках переноса средств из других наук, отсеивании неудачного и в приспосабливании, прилаживании того, что оказалось наиболее подходящим. Главные факторы в этом процессе — время и число проб; в конце концов нужное средство бывает найдено. Основной признак — отсутствие каких-либо общих знаний о средствах и методах, которые бы направляли и регулировали этот поиск.

Второй путь разработки новых средств исследования предполагает теорию самих методов, «методологию». В этом случае специалист-предметник комбинирует не просто что придется, что попало «под руку», а в соответствии с имеющимися у него знаниями о всех существующих в это время средствах и их отношении к задачам. Он пытается перенести не любые средства из других наук, а только те, о которых он знает, что они могут подойти для решения вставших перед ним задач и описания заданных ему объектов; в случае необходимости он создает новые средства, заранее зная, подобно инженеру, создающему машины, какими они должны быть.

Но какой должна быть сама методология науки, ее знания, чтобы обеспечить подобную работу по созданию средств научного исследования?

Существуют две основные точки зрения на этот счет.

Представитель первой точки зрения (ее можно назвать «натурфилософской») считает, что предмет методологии — природа, мир как таковые. С этой стороны методолог, на его взгляд, ничем не отличается от специалиста-предметника. Например, физик анализирует физические процессы в объектах, и ученый, работающий в области методологии физики, тоже должен изучать эти же физические процессы. Разница между ними заключается только в том, что физик будет изучать физические процессы конкретно, опираясь, с одной стороны, на экспериментальные методы, с другой стороны — на аппарат математики, а методолог будет изучать физические процессы «в общем», выделяя их «общие» стороны и свойства. По убеждению натурфилософа, понятия, вырабатываемые при таком «общем подходе» к физическим процессам, могут служить методами для конкретного физического исследования.

Представитель второй точки зрения (ее можно назвать «теоретико-познавательной») считает, что предмет методологии как науки принципиально отличен от предмета всех других конкретных наук; это — деятельность познания, мышление, или, если говорить более точно, вся деятельность человечества, включая сюда не только собственно познание, но и производство. Можно сказать, что методология, на его взгляд, есть теория человеческой деятельности. Именно поэтому методологические знания могут служить руководством при поисках и выработке новых средств научного исследования: ведь они описывают и даже заранее проектируют ту деятельность, которую нужно для этого осуществить.

По-видимому, только теоретико-познавательная точка зрения на методологию оправдывает ее выделение в качестве действительной науки. Чтобы описать условия, в которых выделяются специфически методологические проблемы, рассмотрим в схематизированном виде особые ситуации, складывающиеся в ходе развития науки, — так называемые «антиномии», или «парадоксы».

Их общая логическая схема может быть представлена очень просто. Определенный объект А, являющийся образцом и эталоном класса, анализируется сначала посредством процедуры ?₁ и выступает как обладающий свойством В; потом этот же объект анализируется посредством другой процедуры ?₂ и выступает как обладающий свойством не-В. При проверке обнаруживается, что процедуры выполнены правильно, что они обе в равной мере могут быть применены к этому объекту и при данном уровне развития науки не удается выявить того свойства в объекте, которое обусловливает столь странные результаты исследования. Таким образом, оба знания «А есть В» и «А есть не-В», полученные соответственно с помощью процедур ?₁, и ?₂, оказываются одинаково обоснованными и «правильными», и это создает особую ситуацию «разрыва» в развитии науки.

Уже в древнегреческий период была зафиксирована масса подобных ситуаций (они назывались «апориями») в самых различных науках — в математике, физике, философии.

Например, записывался натуральный ряд чисел, в нем выделялись числа — «полные квадраты»; они сопоставлялись со всем рядом:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16… 1 4 9 16…

Совершенно очевидно, что при таком способе сопоставления чем дальше мы будем двигаться по ряду, тем меньшим будет «вес» полных квадратов по сравнению со всеми другими числами. Из этого делали вывод, что число полных квадратов в ряду натуральных чисел меньше, чем число всех чисел. Но затем предлагался другой способ сопоставления: каждому числу натурального ряда ставился в соответствие его квадрат

1 2 3 4 5 6 7 8 1 4 9 16 25 36 49 64

Было очевидно, что сколько бы мы ни двигались так по ряду, мы всегда сможем это сделать. Из этого делали вывод, что число полных квадратов в бесконечном ряду чисел не меньше числа всех чисел.

Таким образом, применяя два различных способа рассуждения — и заметим: правильных с точки зрения существовавших тогда понятий, — мы приходим к двум различным, взаимно исключающим друг друга утверждениям.

Могут попробовать возразить, что эти утверждения не были правильными, так как к бесконечным множествам, с точки зрения современной математики, не могут применяться понятия «больше», «меньше», «равно», а должны применяться понятия «мощности» и связанные с ними процедуры сопоставления.[75] Это правильно. Но мы знаем это сегодня, а когда этот вопрос встал и когда его обсуждали, начиная, по-видимому, с Демокрита и вплоть до работ Г. Кантора, понятия мощности множества не существовало и приходилось пользоваться теми понятиями, которые были. Кроме того, даже и с этой модернизированной точки зрения нужно признать, что оба утверждения по поводу числа полных квадратов в ряду натуральных чисел находятся в совершенно равных условиях — оба являются одинаково ложными или одинаково истинными. Только это важно в контексте данного рассуждения: возникала ситуация, в которой два знания исключали друг друга и оба были одинаково правильными, и из этой ситуации нужно было выходить, создавая новые средства науки.

Чтобы снять возможное впечатление, будто парадоксальная ситуация возникает из-за оперирования «трудным» и немного мистическим понятием бесконечности, разберем еще пример физического парадокса, выявленного Г. Галилеем примерно через две тысячи лет после появления разобранного выше математического парадокса.

Различие между равномерными и переменными движениями стало известно людям уже давно. Но это было лишь наглядное, чувственное знание, не осмысленное в понятиях. Существовавший во времена Аристотеля чувственно-непосредственный способ сопоставления движений, когда время фиксировалось как равное, а сравнивались одни лишь отрезки пройденного телами пути, не позволял выявить различие между равномерными и переменными движениями в виде понятия.

И хотя в представлении древних понятие скорости было результатом и средством сопоставления движений вообще, независимо от их характера, по содержанию и по своему строению оно служило адекватным отражением только равномерных движений. Поэтому когда Галилей приступил к исследованию ускоренных движений, используя для этого понятие скорости, выраженное в формуле v = s/t, то это привело его к логическому противоречию (антиномии). Так как часы, находившиеся в его распоряжении, несмотря на все произведенные усовершенствования, были все еще малопригодны для измерения небольших промежутков времени, Галилей решил замедлить исследуемые движения падения с помощью наклонных плоскостей, а это в свою очередь заставило его сопоставить между собой падение тел по вертикали и по наклонным. Согласно определениям Аристотеля, из двух движущихся тел то имеет большую скорость, которое проходит за одно и то же время большее пространство, чем другое, или то же пространство, но за меньшее время. Соответственно считалось, что два движущихся тела обладают одинаковой скоростью, если они проходят равные пространства в равные промежутки времени.

Галилея эти определения уже не удовлетворяли. Выработанный им способ измерения времени позволил представить понятие скорости в виде математического отношения величин пути и времени. С этой новой точки зрения ничего не изменится, если назвать скорости равными и тогда, «когда пройденные пространства находятся в таком же отношении, как и времена, в течение которых они пройдены…» [Галилей, 1948, с. 34]. Поскольку Галилей уже «подвел» понятие скорости под более широкое понятие математического отношения, сделанный им переход был вполне законен. Равенство отношений s₁/t₁ = s₂/t₂ как при s₁ = s₂ так и при s_{1 ?} s₂ остается справедливым, если t₁ и t₂ меняются в той же пропорции, что и пути.

Итак, имеются два определения равенства скоростей двух движущихся тел.

Первое: скорости двух тел равны, если за равные промежутки времени эти тела проходят равные пространства.

Второе: скорости двух тел равны, если пространства, проходимые одним и другим, пропорциональны временам прохождения.

Второе определение является обобщением первого. Имея эти два определения, Галилей приступил к сопоставлению конкретных случаев падения тел. Пусть по СВ и СА (см. схему 1) падают два одинаковых тела. Скорость тела, падающего по СВ, будет больше скорости тела, падающего по СА, ибо, как показывает опыт, в течение того времени, за которое первое падающее тело пройдет весь отрезок СВ, второе пройдет по наклонной СА часть CD, которая будет меньше СВ. Отсюда в соответствии с первым определением можно сделать вывод, что скорости тел, падающих по наклонной и по вертикали, не равны.

В то же время известное Галилею положение о том, что скорость падающих тел в какой-либо точке зависит только от высоты их падения, наводят его на мысль, что раз скорости тел в точках А и В, расположенных на одной горизонтали, равны, то они должны быть и вообще равны на отрезках СА и СВ. Он проверяет это предположение на опыте, и действительно оказывается, что отношение времен падения по всей наклонной и по всей вертикали равно отношению длин наклонной и вертикали. Отсюда в соответствии со вторым определением можно сделать вывод, что скорости тел, падающих по наклонной и по вертикали, равны.

Таким образом, следуя рассуждению Галилея, мы получили два противоречащих положения: 1) «Скорости тел, падающих по СА и СВ, равны»; 2) «Скорости тел, падающих по СА и СВ, не равны».

Причину выявленного Галилеем противоречия нельзя искать в произведенном им обобщении условий равенства скоростей. Если бы мы, пользуясь старым условием равенства скоростей, начали сопоставлять движения шаров по СА и СВ, беря отрезки проходимого пути в разных частях СА и СВ, то мы получили бы и при старом определении весьма противоречивые результаты. Скорость падения шара no CB могла оказаться в одном месте больше скорости падения шара по СА, в другом — равной, в третьем — меньшей. Таким образом, рассмотренное развитие понятия скорости и обобщение условий равенства скоростей не являлись причиной противоречия, а были лишь случайными обстоятельствами, которые облегчили его обнаружение.

Причина этого противоречия заключена в том, что понятие скорости, сложившееся из сопоставления равномерных движений и однозначно характеризовавшее эти движения, уже не подходит для сопоставления и однозначной характеристики движений неравномерных.

Подобные логические противоречия, или антиномии, можно часто встретить в истории науки. Оба положения, составляющие антиномию, в равной мере истинны и неистинны. Истинны в том смысле, что они оба действительны, если мы исходим из существовавшего в то время определенного строения исходного понятия. Неистинны в том смысле, что это строение понятия уже не может дать однозначной характеристики новых исследуемых явлений.

Ситуации парадоксов, или антиномий, занимают особое положение в ходе развития науки. Прежде всего в их контексте уже бессмысленно спрашивать: какому из имеющихся знаний соответствует объект, первому или второму. Он не соответствует ни одному из них, он отличен от обоих. Так, благодаря сопоставлению двух исключающих друг друга знаний, относимых к одному объекту, сам объект отделяется от знаний о нем и противопоставляется им как нечто третье, пока не познанное. По выражению Гегеля, сначала в понятии мы видели сам объект, теперь понятие как форма отделяется от объекта. Это первый и, наверное, основной шаг в формировании теоретико-познавательной точки зрения на мир.

Выделение объекта как чего-то отличного от того, что мы видим в знании, и сопоставление знаний друг с другом заставляет сделать следующий шаг и поставить вопрос: чем обусловлено это различие знаний. При ответе на этот вопрос выявляется следующий элемент предмета теории познания: процедуры получения знаний, процедуры познавательной деятельности. Именно в них находят ту причину, которая привела к различию знаний об объекте.

Появление теоретико-познавательной точки зрения делает возможным и собственно методологический подход в разработке средств науки.

Дело в том, что в каждой ситуации могут быть поставлены две разные задачи и в соответствии с этим как практическая, так и исследовательская деятельность могут идти по двум принципиально различным линиям и опираться на различные методы. В одном случае исследование будет направлено на преодоление именно этой, единичной антиномии, на выработку нового специального понятия, «снимающего» антиномию. В другом — оно может быть направлено на выяснение условий появления антиномий вообще (а не только этой единичной), на анализ путей и методов их преодоления, на выяснение структуры вновь получаемого знания в его отношении к прежним, антиномичным.

В первом случае мы будем оставаться в рамках данной специальной науки, математики, физики или химии, будем пользоваться ее специфическими методами. И при этом каждая новая антиномия будет вставать перед нами такой же проблемой, как и предыдущая, и мы будем подходить к ее решению вооруженными так же, как мы были вооружены при решении первой. Наш опыт преодоления антиномий никак не будет осознаваться и не будет влиять на последующую деятельность.

Во втором случае необходимо выйти за границы той или иной специальной науки и выделить совсем особый предмет рассмотрения — знания об объектах, процессы выработки и использования их. Здесь придется прибегнуть к совершенно иным методам исследования, выработать понятия принципиально иного рода, нежели понятия той или иной специальной науки; и это будут понятия методологии (в широком смысле этого слова, включая туда логику и теорию познания).

Антиномии, или парадоксы, возникающие в ходе развития науки, были взяты нами в качестве примера ситуаций, которые делают необходимой постановку собственно методологических задач. В этих ситуациях фактически формируется и выделяется та действительность, которая становится предметом методологии как науки. Эта действительность — деятельность по получению знаний.[76]

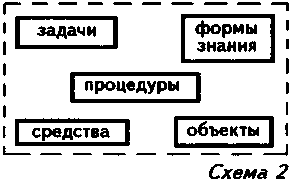
Мы можем изобразить ее строение в блок-схеме, если выделим и перечислим основные составляющие всякой деятельности. Специальный анализ показывает, что в любой акт познавательной деятельности обязательно входят: 1) задачи (или требования), 2) объекты, 3) средства, 4) формы знаний и 5) процедуры, создающие их (см. схему 2).

Эту схему можно рассматривать как первое приближенное изображение предмета методологических исследований.

Очень важно также подчеркнуть, что постановка вопроса об объекте как таковом, в отличие от «данности» его в той или иной форме знания, появляется впервые отнюдь не в специально-научных исследованиях, как это обычно думают, а только в методологическом анализе. В специально-научных исследованиях, где имеется одно или несколько легко соединимых друг с другом знаний об объекте, не возникает вопросов об объекте как таковом и нет нужды противопоставлять его знаниям. Мы уверены, что объект таков, каким он дан нам в этих «знаниях». Только в ситуациях антиномий и аналогичных им нам приходится выделять объект, ставить вопрос о его природе и стараться изобразить его как таковой, в форме, отличной от всех уже существующих о нем знаний [1964 h *, I]. Поэтому именно методология и теория познания, как это ни странно на первый взгляд, оказываются учением об объектах и областях объектов, т. е. обязательно включают в себя моделирующую мир онтологию.[77] Поэтому ошибочным является тезис, время от времени всплывающий в философской литературе, что де теория познания и логика являются наукой о деятельности и процессах познания, & не о мире. Это противопоставление неправомерно: она является наукой о деятельности познания и тем самым о мире, включенном и включаемом в нее. Само это противопоставление было обусловлено неправильным пониманием объективности — был забыт знаменитый тезис К. Маркса: «Главный недостаток всего предшествующего материализма — включая и фейербаховский — заключается в том, что предмет, действительность, чувственность берется только в форме объекта, или в форме созерцания, а не как человеческая чувственная деятельность, практика, не субъективно» [Маркс, 1955 b, с. 1].

Но это представление объектов в методологии существенно отличается от их представления в специальных науках: оно создается как изображение их «высшей» объективности, освобожденной от частной формы тех или иных специальных задач. По этой же причине методологическая онтология не имеет ничего общего с натурфилософией: она существует в системе методологии и создается не на основе анализа физической, химической или какой-либо иной эмпирии, а на основе анализа человеческой деятельности — производства (практики) и мышления.

Таким образом, переходя в область методологического исследования, мы формируем совершенно особый предмет, который не совпадает с предметом ни одной частной науки. И мы можем исследовать и описывать этот предмет только с помощью особых методов, не сводимых к методам специальных наук.

О том, что это утверждение не является общепризнанным, что вокруг него сейчас еще идет борьба, говорит хотя бы широко распространенный и принятый многими тезис Д. Гильберта, что обоснование математики есть дело самой математики [Гильберт, 1948, с. 391, 363–364; Клини, 1957, с. 55, 58]. И не только математики, но и представители многих других наук разделяют и поддерживают тезис, что методологию специальных наук должны разрабатывать представители самих этих наук. Поэтому формулируя положение, что методология науки имеет свой особый предмет и использует свои особые методы — только в этом случае она будет действительной наукой, — мы противопоставляем его положению, что методологические проблемы каждой науки могут решаться методами самой этой науки. На наш взгляд, торжество такого подхода приводило всегда только к уничтожению самой методологии как науки. И то, что его нередко принимали, объясняется лишь одним — тем, что он избавлял от необходимости разрабатывать особые методы методологии науки. Отвергая этот тезис, мы сталкиваемся с этой проблемой во всей ее остроте: что представляют собой и какими должны быть основные средства методологии или теории деятельности. Одним из них является

различение объекта и предмета знания

Объект существует независимо от знания, он существовал и до его появления. Предмет знания, напротив, формируется самим знанием. Начиная изучать или просто «включая» в деятельность какой-либо объект, мы берем его с одной или нескольких сторон. Эти выделенные стороны становятся «заместителем» или «представителем» всего многостороннего объекта; они фиксируются в знаковой форме знания. Поскольку это — знание об объективно существующем, оно всегда объективируется нами и как таковое образует «предмет». В специально-научном анализе мы всегда рассматриваем его как адекватный объекту. И это правильно. Но при этом надо всегда помнить — а в методологическом исследовании это положение становится главным, — что предмет знания не тождествен объекту: он является продуктом человеческой познавательной деятельности и как особое создание человечества подчинен особым закономерностям, не совпадающим с закономерностями самого объекта.

Одному и тому же объекту может соответствовать несколько различных предметов. Это объясняется тем, что характер предмета знания зависит не только от того, какой объект он отражает, но и от того, зачем этот предмет сформирован, для решения какой задачи.

Чтобы пояснить эти общие абстрактные определения, рассмотрим простой пример.

Предположим, что у нас в двух населенных пунктах имеются две группы баранов (схема 3). Это, бесспорно, объекты. Люди имеют с ними дело, разным образом используют их, и в какой-то момент перед ними встает задача пересчитать их. Сначала пересчитывается одна группа, положим — 1, 2, 3, 4, затем вторая — 1, 2, 3, 4 и наконец оба числа складываются: 4 + 4 = 8.

И уже в этом простом факте выступает ряд очень сложных и вместе с тем очень интересных моментов. Объекты, бараны, имеют целый ряд сторон и когда мы их начинаем считать, то выделяем одну сторону каждой группы — количество баранов. Это количество мы выражаем в значках, в цифре 4 один раз, затем в цифре 4 второй раз, а потом производим какое-то странное действие — мы складываем числа. Если бы у нас были не две группы, а, скажем, пять, и в каждой из них было бы по 4 барана, то мы не складывали бы, а просто умножали числа: 4 х 5 = 20, т. е. произвели бы другое, еще более странное действие.

Почему я их все время называю странными? Давайте спросим себя, может ли быть применено действие сложения к баранам как таковым? Или, скажем, действие умножения? Или — продолжим эту линию рассуждения — действия деления, извлечения корня, возведения в степень? Бесспорно, нет.

Но есть и еще одна, не менее важная сторона дела. Мы должны спросить себя: разве эти действия — сложение, умножение, возведение в степень — применяются к «закорючкам», выражающим знаки, к цифрам? Когда мы складываем, то складываем не цифры, а числа. И есть большая разница между цифрой и числом, потому что цифра — это просто значок, след от чернил, краски, мела, а число есть образование совершенно особого рода, это — значок, в котором выражена определенная сторона объектов. И мы складываем числа не потому, что они значки, точно так же как мы умножаем их не потому, что они цифры; мы складываем и умножаем, потому что в этих значках выражена строго определенная сторона объектов, именно — количество. В них она получила самостоятельное существование, отдельное от объектов, и в соответствии с этим когда мы говорим о числе как особом образовании, отличном от баранов как таковых и от количества баранов, то имеем в виду не объект и не стороны этого объекта, а особый, созданный человечеством «предмет».

Этот предмет такая же реальность, как и исходные объекты, но он имеет совершенно особое социальное существование и особую структуру, отличную от структуры объектов. Сами по себе цифры — еще не предмет. Но точно так же и объекты — это еще не предмет. Предмет возникает и начинает существовать, когда процедура сопоставления выделяет в группе баранов количество и выражает его в значках чисел. То, с чем мы имеем дело, это, таким образом, связка или отношение замещения между баранами, взятыми в определенном сопоставлении, и знаковой формой чисел; но оно объективно существует и выражено только в этой знаковой форме и способах деятельности с нею. Предмет знания — реальность, но законы деятельности с ней как с реальностью — особые законы; с баранами мы действуем одним образом, с числами мы действуем и должны действовать совершенно иначе. И только выразив количество баранов в особой знаковой форме, мы получили возможность действовать с ним особым образом, именно как с количеством, а не как с баранами. Раньше мы не могли этого делать, мы должны были действовать с баранами, как это полагается по их природе и сути, в крайнем случае мы могли их пересчитать.

В самом по себе объекте никакого предмета не содержится. Но он может быть выделен как особое содержание посредством практических и познавательных действий с объектом. Это содержание может быть зафиксировано в знаках. И коль скоро это происходит, возникает предмет и предстает перед человеком в объективированном виде как существующий помимо тех объектов, от которых он был абстрагирован. Его объективированная «данность» порождает иллюзии — как будто бы имеют дело с самим объектом. Это иллюзорное понимание сути дела, возникнув уже в сравнительно простых ситуациях (например, с количеством), проникает затем в высшие этажи науки и там запутывает все окончательно.

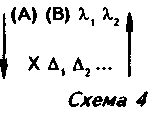
Есть единственный путь понять природу предмета — это выяснение механизмов era образования и структуры, а это означает и анализ его как последовательно надстраивающихся друг над другом плоскостей замещения.

Простейший вид предмета может быть представлен в схеме 4.

Здесь первую плоскость образует оперирование с объектом X посредством процедур ?₁, ?₂… Результаты такого оперирования выражаются в знаках (А) (В), которые фиксируют и замещают выделенное в первой плоскости содержание Х ?₁ ?₂… Эти знаки включены в особую деятельность ?₁ ?₂ — формальное оперирование со знаками, — и все это вместе образует вторую плоскость. Результаты преобразования знаковой формы во второй плоскости относятся к объекту X. Исходное замещение и обратное отнесение изображены на схеме стрелками.

Знаковые образования (А) (В) и применяемые к ним операции ?₁ ?₂ сами могут образовать новую исходную плоскость, к которой применяются новые содержательные действия сопоставления (скажем, ? ₁,? ₂…); иначе говоря, сами знаки становятся объектом следующей деятельности. В этом случае результаты оперирования во второй плоскости фиксируются в знаковых образованиях (G) (E) (D), которые образуют следующую, третью плоскость замещения, причем оперирование со знаками здесь осуществляется посредством особых процедур ?₁?₂… В дальнейшем может образоваться еще одна или ряд плоскостей, так что в конечном счете мы получаем иерархию отношений замещения, которая может быть изображена в схеме 5.

Таким образом, мы можем сказать, что «предмет» это — иерархированная система замещений объекта знаками, включенными в определенные системы оперирования (см. по этому поводу наши статьи [1960 а; 1964с *]), в которых эти системы замещения существуют реально как объекты особого рода, они опредмечиваются в виде научной литературы или производственной деятельности общества по созданию и использованию знаковых систем. Подрастающее поколение непрерывно «приобщается» к этим системам замещения, усваивает их, а затем строит свою деятельность на основе их.

Проведенное таким образом различение объекта и предмета знания позволяет ввести еще одно важнейшее понятие методологии:

онтологическое представление содержания знания

Важнейшим результатом предшествующего анализа было положение о том, что применение действий сопоставления к объектам создает новое содержание; мы изобразили его символами Х?₁?₂… Это содержание фиксируется, выражается в знаковой форме (А) (В) и способах оперирования с нею — ?₁?₂. Применяя затем другие действия сопоставления к знакам (А) (В), мы получаем новое содержание, которое выражаем в знаках (D) (E) (F) и очень часто относим непосредственно к объекту X. Например, мы измеряем последовательно соответствующие друг другу значения давления и объема определенной массы газа (первая плоскость предмета), получаем ряды значения р₁, р₂, р₃… V₁, V₂, V₃… (образующих вторую плоскость предмета), затем сопоставляем их как p₁V₁<->p₂V₂<->p₃V₃<->… и находим математическую форму их зависимости pV = const (которая должна быть помещена уже на третьей плоскости предмета). Содержание этой формы мы рассматриваем как «закон», которому подчиняется газ, и, следовательно, относим его непосредственно к нашему объекту.

Но нередко такое непосредственное отнесение не может быть выполнено, так как содержание, выявляемое опосредованно из деятельности со знаками, не соответствует эмпирически наблюдаемым или выявляемым свойствам объекта. Тогда для него строят специальное знаковое изображение, которое «встает» как бы между знаковой формой знания и эмпирически данными объектами.

Если обратиться к приведенной выше схеме «предмета», то ситуацию, в которой вновь полученное знание не удается отнести к объекту, можно будет изобразить в схеме 6.

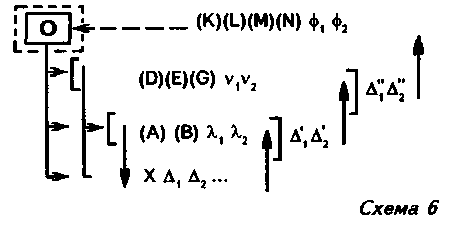
Здесь в очерченном пунктиром прямоугольнике изображен «разрыв», возникший из-за того, что мы не можем отнести результаты, полученные при оперировании в четвертой плоскости знания, непосредственно на объект X. Для ликвидации этого разрыва строится особая знаковая конструкция (на схеме она изображена маленьким квадратом с буквой О в середине), которая должна определенным образом представить предмет «как таковой». Исходя из этой специфической функции, о подобных изображениях можно говорить как об онтологических представлениях содержаний знания. Это точно выражает специфическую познавательную роль таких знаковых конструкций: они должны так представить объект, чтобы обеспечить связь его с вновь полученными знаниями. Именно таким путем появляются так называемые «идеальные предметы» — тяжелая точка, идеальный рычаг, абсолютно упругое тело, математический маятник и др. [Хайкин, 1947].

Рассмотрим в качестве примера «математический маятник». Уравнение его колебаний содержит знаки М — массы маятника и l — его длины. Представим себе, что перед нами реальные маятниковые часы с массивным диском и длинным стержнем. Можно ли применить это математическое уравнение колебаний маятника для описания реального движения маятника часов? Оказывается, что если мы будем измерять его действительные параметры — длину стержня или массу диска, то получим неправильные результаты. Математическое уравнение колебаний маятника может быть отнесено непосредственно лишь к особому идеальному предмету — «математическому маятнику», а он, в свою очередь, может быть представлен только в знаках. Чтобы применить математическое уравнение колебаний маятника к реальному маятнику, последний нужно еще свести к математическому маятнику, а это значит, с помощью особых специально задаваемых процедур измерить и рассчитать так называемые «приведенную длину» и «приведенную массу» реального маятника (см. схему 7).

Аналогичная картина с онтологическими представлениями обнаруживается и у всех других научных знаний.

Онтологическое представление дает вторую форму существования предмету знания: оно как бы «сплющивает» его многоплоскостную структуру в одном изображении.

Только теперь, введя эти общеметодологические понятия, мы можем вернуться к проблемам системно-структурного исследования и спросить:

что такое система?

Термин «система» определяется с помощью таких терминов, как «связь» (или «взаимосвязь»), «элемент», «целое», «единство». В чисто словесных формулировках еще можно встретить согласие, но представители разных наук вкладывают в эти слова столь различный смысл, что на деле согласие их является лишь видимым: для одних «связь» это просто геометрические взаимоотношения частей; для других — зависимость между частями или сторонами целого; одни будут называть «структурой» геометрическое взаимоотношение, другие сведут ее к «набору» элементов. Часто теоретические определения расходятся с эмпирическим материалом. Так, например, известный английский кибернетик Ст. Бир называет системой взаимосвязь самых различных элементов, а в качестве примера приводит бильярд, в котором никаких взаимосвязей фактически нет, а есть только функциональное единство целого [Вир, 1963, с. 22]. Поэтому, наверное, самым правильным было бы сказать, что в настоящее время вообще не существует удовлетворительных, достаточно широко принятых понятий системы и структуры. Не смогло предложить таких понятий и общество по разработке «общей теории систем». Г. Х. Гуд и Р. Э. Макол, анализирующие системы «большого масштаба», отказываются предпринимать какие-либо попытки точно определить границы, очерчивающие рассматриваемые ими системы. «Как обычно бывает в любой области, — замечают они, — эти границы проходят по широким неопределенным территориям и поиски их точного положения вызвали бы большие, но бесплодные споры» [Гуд, Макол, 1962, с. 17]. И фактически выраженная ими позиция является единственной широко распространенной среди тех, кто исследует конкретные системы и структуры.

Ее бессмысленно оспаривать, если заранее известно, что в данный момент у ваших оппонентов все равно нет средств, чтобы решить проблему. Но и только. Вряд ли стоит специально доказывать, что неограниченность и расплывчатость исходных понятий крайне затрудняет научное исследование и делает его фактически малопродуктивным.

Наверное, в этой ситуации полезно поставить вопрос: почему все попытки выделить специфические признаки систем в течение столь долгого времени не дают положительного результата? Ответ на него в каком-то смысле банален: по-видимому, пытаются объединить в одном классе слишком разнородные явления, не видят, ухватившись за формальные и вместе с тем лишь интуитивно понятые характеристики целого и составляющих его элементов, более существенных и глубоких различений, действительно определяющих природу и жизнь «систем».

Немалую роль в установке исследовать «системы вообще» играет и ложная методологическая догма, что-де всегда надо стремиться к выделению из массы разнородных явлений общих инвариантов в ущерб эмпирическому движению к деталям и обусловленному им ограничению.

По-видимому, здесь единственно эффективным путем теоретической разработки проблемы должен быть путь разграничения и разделения охватываемого исследованием эмпирического материала на более узкие области, выделяемые по каким-то другим, несистемным, но более важным для объектов признакам.

В частности, нужно провести исключительно важное и принципиальное различение систем на

«организации» и «структуры»

Даже при наличии всех обычно перечисляемых признаков систем сложные объекты могут не иметь друг с другом ничего общего именно в «системном» отношении. Покажем это на простых моделях.

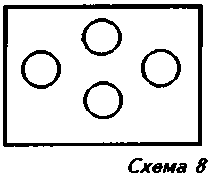
Представим себе деревянную основу, на которой в специально выдолбленных ячейках лежат шарики (схема 8).

Шарики прочно занимают свои места и все вместе они образуют строго определенную конфигурацию. Эта конфигурация может быть описана с помощью тех или иных «целостных» характеристик, например, можно установить ее ромбовидный характер. Каждый шарик имеет свое строго определенное место, свою позицию и жестко определен в своем отношении как к целому, так и к другим шарикам. Если убрать один из шариков, то целое, бесспорно, изменится: вместо ромбовидной конфигурации мы будем иметь треугольную. Следовательно, эти четыре шарика образуют некоторое единое целое: изменение места по крайней мере одного шарика или его исчезновение изменяет целое. Но вот важная особенность: изменение в положении одного шарика никак не сказывается на положении других. С изменением положения одного шарика происходит изменение целого, хотя оставшиеся его элементы остаются неизменными. Указанные свойства определяют класс систем одного из простейших типов, а именно — организации с отношениями. В такого рода системных образованиях отсутствуют связи.

Возьмем другой пример. На такой же самой деревянной основе поместим шарики в той же ромбовидной конфигурации, но, в отличие от первого примера, свяжем их друг с другом и с основой пружинками (схема 9).

Когда пружинки уравновешены, вся система покоится и четыре шарика образуют ромбовидную конфигурацию. Изменим положение одного из шариков. При этом, конечно, изменится общая конфигурация системы, но не так, как это было в предыдущем случае: система пружин, выведенная из равновесия в результате изменения положения одного из шариков, придет в движение, все остальные шарики сместятся, появится совершенно новая конфигурация. Как и в первом случае, произошло изменение целого, но теперь уже — за счет изменения положения всех элементов. В этом особенность систем второго типа: их элементы не только относятся друг к другу, но они также и связаны между собой. Именно поэтому изменение положения одного из шариков влечет за собой изменение положения других. Таким образом, в этом случае мы имеем принципиально иной тип систем — системы связей, или структуры.

Но это различение типов систем по основанию «отношение — связь» отнюдь не единственное. Не меньшую роль играет также различение их на

системы знания и системы объекта

В подавляющем большинстве современных работ по проблемам структур и систем или по методологии структурно-системного исследования эти принципиальные различения не проводятся. Система знания об объекте отождествляется в них обычно с системой предмета, а система предмета затем механически накладывается на систему объекта. В дальнейшем этой, фактически одной, системе даются разные трактовки: то она выступает как система знания, то как система объекта, отраженного в этом знании. И даже непрерывно возникающие из-за этого антиномии не могут разрушить веру в единство и совпадение этих трех систем.

В лингвистике, например, постоянно употребляют как синонимы выражения «системы знаний о языке», «системы языка», «системы языка как объекта языкознания» и доказывают, что система предмета не может отличаться от системы объекта (см., например, [О соотношении… 1960, с. 95, 102, 125 и др.]).

Такое же положение отчетливо обнаруживается в кибернетике. У. Р. Эшби в работах 50-х годов не мог представить себе систему иначе, как совокупность связанных между собой параметров. Ст. Бир в противоположность Эшби, казалось бы, все время говорит о системах объектов, но на поверку оказывается, что это те же системы предметных онтологических изображений, которые лишь в чисто словесном плане получают объектную интерпретацию.

Между тем системы знания, предмета и объекта совершенно очевидно не совпадают друг с другом и ни в коем случае не могут отождествляться.

Научное знание всегда системно. Уже простейшие виды знания, такие, как «береза — белая», «металл — электропроводен» и т. п., представляют собой системы; форма их состоит из элементов, связанных друг с другом, а вместе с тем и содержание выступает расчлененным и одновременно связанным в некоторое единство. И какие бы другие более сложные виды знаний мы ни брали — отдельные положения или целые теории, — они всегда будут системными. Разница заключается только в виде и сложности самих систем.