Глава 13 ОБ ИЗМЕНЕНИЯХ, ПРЕТЕРПЕВАЕМЫХ МАКСИМАЛЬНОЙ И БЕСКОНЕЧНОЙ ЛИНИЕЙ

Глава 13

ОБ ИЗМЕНЕНИЯХ, ПРЕТЕРПЕВАЕМЫХ МАКСИМАЛЬНОЙ И БЕСКОНЕЧНОЙ ЛИНИЕЙ

Итак, я утверждаю, что если бы существовала бесконечная линия, она была бы прямой, она была бы треугольником, она была бы кругом, и она была бы шаром; равным образом, если бы существовал бесконечный шар, он был бы кругом, треугольником и линией; и то же самое надо говорить о бесконечном треугольнике и бесконечном круге.

Во-первых, что бесконечная линия будет прямой, очевидно: диаметр круга есть прямая линия, а окружность – кривая линия, большая диаметра; если эта кривая тем меньше в своей кривизне, чем большего круга окружностью она является, то окружность максимального круга, больше которого не может быть, минимально крива, а стало быть, максимально пряма. Минимум совпадает таким образом с максимумом. Даже и на глаз видно, что максимальная линия с необходимостью максимально пряма и минимально крива. Здесь не может оставаться ни тени сомнения, когда мы рассмотрим на фигуре сбоку, что дуга CD большего круга больше отступает от кривизны, чем дуга EF меньшего круга, а та больше отходит от кривизны, чем дуга GH еще меньшего круга, почему прямая линия AB будет дугой максимального круга, который уже не может увеличиться. Так мы видим, что максимальная и бесконечная линия по необходимости совершенно прямая и кривизна ей не противоположна; мало того, кривизна в этой максимальной линии ость прямизна. Это первое, что требовалось доказать.

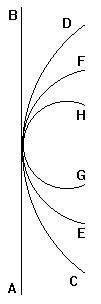
Во-вторых, как сказано, бесконечная линия есть максимальный треугольник, круг и шар. Для доказательства этого надо рассмотреть на конечных линиях, что заключено в возможности конечной линии; поскольку все, чем конечная линия является в возможности, бесконечная линия есть в действительности, мы сможем увидеть искомое еще яснее.

Мы знаем прежде всего, что конечная линия по своей длине может быть длиннее и прямее; а уже доказано, что максимальная линия – самая длинная и прямая. Потом, если линия AB будет обведена вокруг неподвижной точки A, пока не придет в C, возникнет треугольник. Если вращение будет совершаться, пока B не придет в свое начальное положение, возникнет круг.

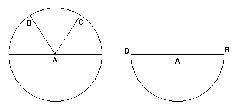
Опять-таки, если В будет обведено вокруг неподвижного A до точки, противоположной своему начальному положению, то есть до D, то из линий AB и AD образуется одна непрерывная линия и будет описан полукруг. Наконец, если этот полукруг будет обведен вокруг неподвижного диаметра BD, то получится шар. И этот шар – последняя возможность линии, целиком переходящей в нем в действительность, потому что шар уже не заключает в себе возможности никакой последующей фигуры.

Поскольку, таким образом, в возможности конечной линии заключены все эти фигуры, а бесконечная линия есть действительным образом все то, возможность чего представляет конечная, то, следовательно, бесконечная линия есть и треугольник, и круг, и шар, что и следовало доказать.

Так как ты, наверное, захочешь яснее убедиться, что бесконечное есть действительность всего, что заключено в возможности конечного, дам тебе совершенно удостовериться в этом.