Упрощающие предположения: q – константа и момент остановки определяется одним условием

Допустим, что q – константа, q = 1, и упростим условие момента остановки, определив его как отсутствие убытков в прошлые периоды, 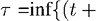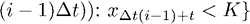, что ведет к

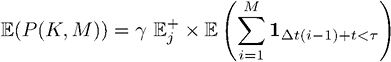
Поскольку выплаты агенту независимы и одинаково распределены, ожидание в момент остановки соответствует ожиданию момента остановки, помноженному на ожидаемое вознаграждение агенту 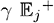. Отсюда .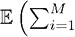

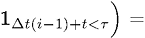
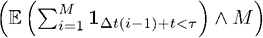Ожидание момента остановки выражается через вероятность успеха при условии отсутствия убытков в прошлом:

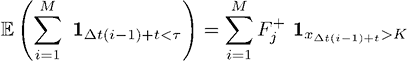
Мы можем записать условие момента остановки в виде непрекращающихся периодов успеха. Пусть ? – упорядоченное множество последовательных периодов успеха ? ? {{F}, {SF}, {SSF}, …, {(M – 1) последовательных S, F}}, где S – успех, а F – неудача за период ?t, со связанными вероятностями ,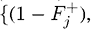

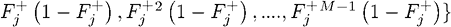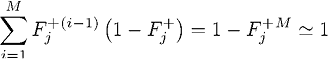
М велико, и, поскольку 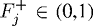, мы можем считать предыдущую формулу почти равенством, так как

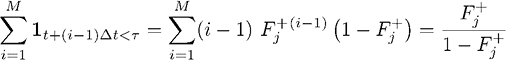
Наконец, ожидаемая выплата агенту составит:

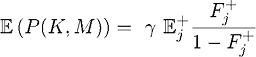
и ее можно увеличить, 1) увеличив 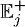 и 2) минимизировав вероятность потери 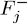, даже если, и это ключевой момент, условия 1) и 2) выполняются за счет m, совокупного ожидаемого от пакета.

Не может не тревожить следующее: поскольку 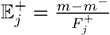, агент не беспокоится об уменьшении совокупной ожидаемой отдачи m, если это проявляется в левой части распределения, m^–. В скошенном пространстве ожидаемая отдача агента максимизируется при распределении j с минимальным значением v_j (максимальная отрицательная асимметрия). Совокупное ожидание положительной мотивации без шкуры на кону зависит от отрицательной скошенности, а не от m.

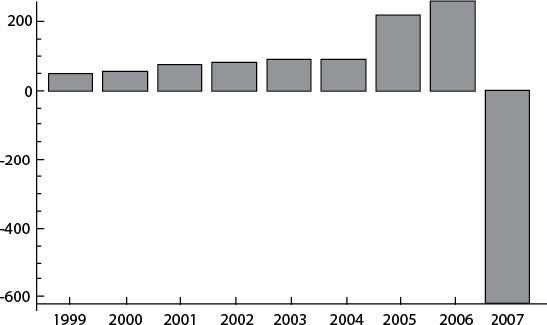
Рис. 8. Indy Mac, компания, потерпевшая банкротство во время кризиса ненадежных кредитов (Taleb 2009). Пример характеризует риски, которые при отсутствии убытков постоянно увеличиваются – вплоть до внезапной катастрофы