Модификация теоремы 1 для броуновского движения

Следствия из упрощенного случая не меняются при переходе к более сложным моделям, таким, как полный стохастический процесс с барьером поглощения. Конечно, в естественной среде может произойти не просто остановка, но прекращение всей предшествующей жизни вообще (X_t может принять крайнее отрицательное значение). Довод Питерса и Гелл-Манна разгадывает также так называемую загадку премии за приобретение акций: вспомним о жирных хвостах (результаты куда сильнее подталкивают эквивалент определенного уровня к катастрофе) и отсутствии взаимозаменяемости времени и ансамбля. Никакой загадки тут нет.

У проблемы есть инвариант в реальной жизни: стохастический процесс типа броуновского движения с поглощающим барьером. Вместо упрощенного примера мы получим для процесса, подверженного риску L, которому соответствует поглощающий барьер снизу, в арифметической версии:

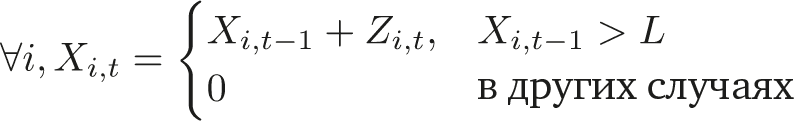
или в геометрической версии:

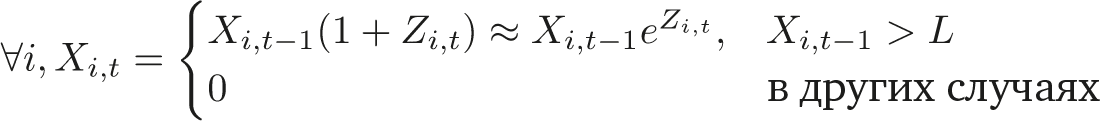
где Z – случайная переменная.

При переходе к непрерывному времени в геометрической версии пусть 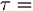 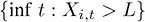– момент остановки. Идея в том, что простое ожидание момента остановки соответствует сроку оставшейся жизни – или характеризует его по порядку величины.

Мы сместили фокус с вероятности на несоответствие между моментом остановки ? для катастрофы и сроком оставшейся жизни.