А. Шкура на кону и хвостовые вероятности

В этом разделе мы проанализируем вероятностную нестыковку хвостовых рисков и отдачи в присутствии проблемы принципала – агента.

Перенос ущерба. Если агент получает прибыль от положительной отдачи в форме случайной величины, но не терпит убытков от отрицательной и оценивается исключительно на базе прошлых результатов, он мотивирован скрывать риски в левом хвосте, используя отрицательно скошенное (или, в более общем виде, асимметричное) распределение результатов. Ситуацию можно обобщить на любую отдачу, в отношении которой агент не несет полные риски и огражден от отрицательных последствий своих действий.

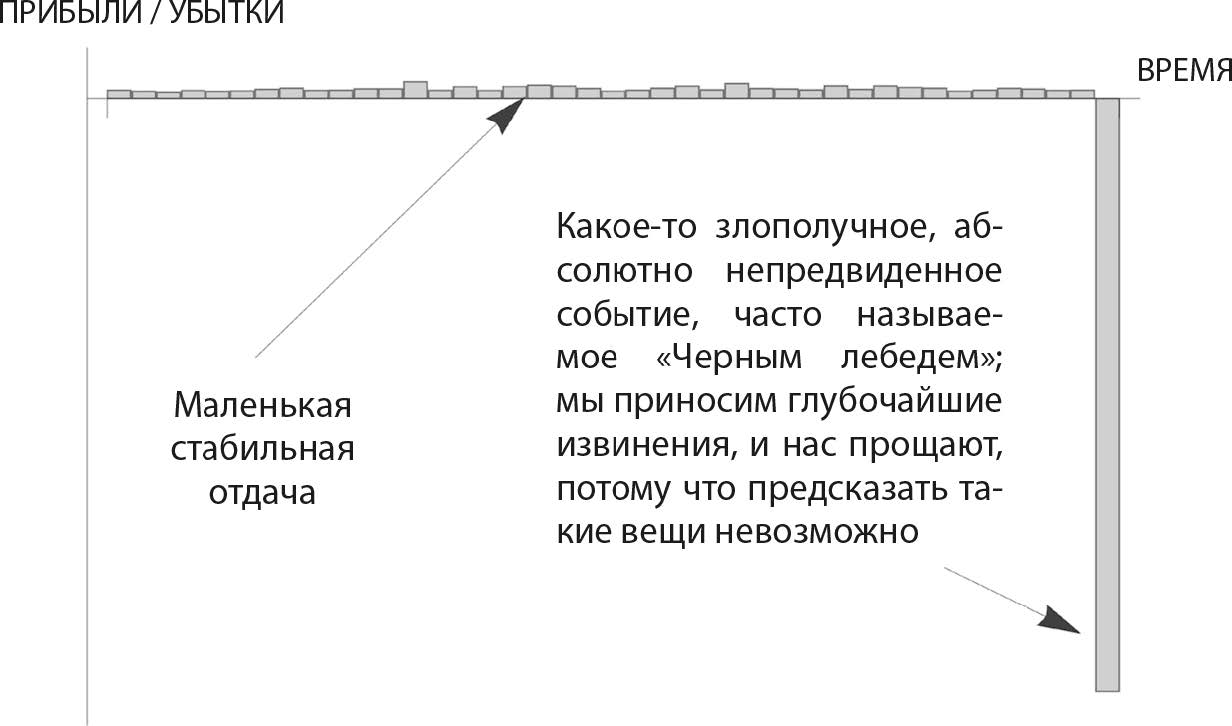
Рис. 7. Бизнес Боба Рубина. Отдача в скошенной ситуации, когда выгода видима (и таит в себе вознаграждение), а ущерб возникает редко (и тот, кто его нанес, не страдает благодаря тому, что не ставит шкуру на кон). Может наблюдаться в политике и везде, где штраф за ущерб мал

Пусть P(K, M) – отдача (выплаты) для оператора над М периодами мотивации:

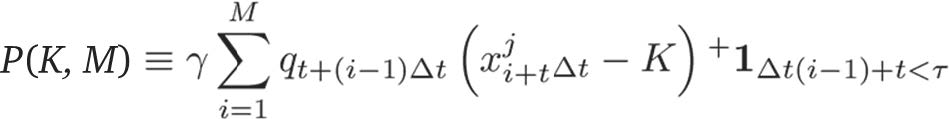
где 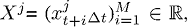 – независимые, одинаково распределенные случайные величины, представляющие распределение прибыли в определенный период 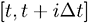, 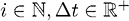и К – «перегородка»:  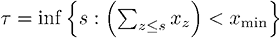– характеристическая функция момента остановки, в который условия прошлых результатов не удовлетворяются (а именно – условие достижения определенных результатов за некое число лет; при невыполнении условия отдача прекращается, игра завершается, количество положительных мотиваторов обнуляется). Константа  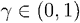– «агентская выплата», ставка вознаграждения за результаты, не обязательно выраженная в деньгах (при условии, что ее можно определить как «выгоду»). 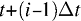Величина  определяет меру риска в момент  (вследствие сдвига Ито: результат в период s определяется через q в определенный более ранний период < s).

Пусть 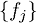 – семейство вероятностных мер  на 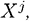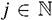. Каждой мере соответствует характеристика среднего/скошенности, так что мы можем разделить их свойства на две части по обе стороны параметра «центральности» К на «верхнее» и «нижнее» распределение. Запишем  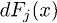как 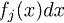, тогда  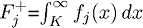и 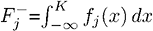  – «верхнее» и «нижнее» распределение, каждое соответствует определенному условному ожиданию  и .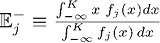

Определим 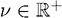 как К-центрированную непараметрическую меру асимметрии, 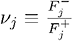, со значениями >1 для положительной асимметрии и <1 для отрицательной. Как можно видеть, при скошенности вероятность и ожидание движутся в разных направлениях: чем больше отрицательная отдача, тем меньше вероятность вознаграждения.

Мы не предполагаем «честную игру», иначе говоря, при неограниченной отдаче 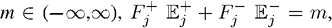 что можно записать как m⁺ + m^–= m.