Г. Специальное определение жирных хвостов

Вероятностные распределения варьируются от тонкохвостых (Бернулли) до чрезвычайно жирнохвостых. Некоторые категории распределений, часто выделяемые по свойствам сходимости моментов: 1) с областью определения, которая компактна, но не вырождена; 2) субгауссово; 3) гауссово; 4) субэкспоненциальное; 5) степенное со степенью больше 3; 6) степенное со степенью меньше либо равной 3 и больше 2; 7) степенное со степенью меньше либо равной 2. В частности, у степенных распределений есть конечное среднее, только если степень больше 1, и конечная дисперсия, только если степень больше 2.

Нас интересует, как в случае, когда хвостовые события чреваты сильными воздействиями, формально определить границу между категориями распределений Среднестана и Крайнестана. Естественная граница между ними проходит по субэкспоненциальному распределению, у которого есть следующее свойство:

Пусть Х = 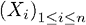 – последовательность независимых и одинаково распределенных случайных переменных (область распределения –  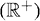с кумулятивной функцией распределения F. Субэкспоненциальный класс распределений определен в Teugels 1975, Pitman 1980:

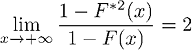, где  – кумулятивное распределение Х₁ + Х₂, суммы двух независимых копий Х. Иначе говоря, вероятность того, что сумма Х₁ + Х₂ превысит значение х, в два раза больше вероятности того, что любая из этих величин превысит х. Следовательно, всякий раз, когда сумма превышает х и значение х достаточно велико, значение суммы достигается за счет какого-то одного слагаемого, превосходящего х – максимума по двум переменным, – а вклад другого слагаемого ничтожен.

В более общем виде можно показать, что в сумме n переменных аналогичным образом доминирует максимум значений по этим переменным. Формально субэкспоненциальному условию эквивалентны два следующих свойства (см. Chistyakov 1964, Embrechts et al. 1979). Для любого n ? 2 пусть 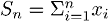 и M_n= max ,

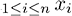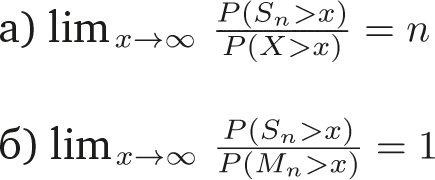
Следовательно, сумма S_n – того же порядка, что и наибольшая выборка M_n, а это – еще один способ сказать, что нет ничего важнее хвостов.

Можно предположить, что хвостовые события в экспоненциальных распределениях «худеют» медленнее, чем в экспоненциальном распределении, для которого жирные хвосты не должны иметь значения. В самом деле, легко показать, что в субэкспоненциальных распределениях нет экспоненциальных моментов:

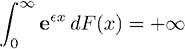
для значений ? больше нуля. Однако обратное неверно: в распределении может не быть экспоненциального момента, однако оно может не удовлетворять условию субэкспоненциальности.

Отметим, что, если рассмотреть отклонения в области отрицательных значений переменной х, мы получим тот же результат по симметрии для экстремальных отрицательных значений, заменив х ? +? на х ? –?. Для переменных с двумя хвостами мы можем рассматривать положительные и отрицательные значения отдельно.