Простой категорический силлогизм

§ 9. Цель силлогизма, как и всякого другого умозаключения, состоит в получении из посылок нового суждения, или вывода. При этом мыслимое в выводе отношение между субъектом и предикатом вывода устанавливается не прямо. Отношение это не видно непосредственно ни из первой, ни из второй посылки, отдельно взятых. Отношение это выясняется для мысли только после сопоставления обеих посылок силлогизма. Сопоставляя посылки, мы рассматриваем отношение субъекта и предиката вывода к некоторому третьему понятию. Только через отношение этого третьего понятия к субъекту вывода и к предикату вывода выясняется отношение между субъектом и предикатом вывода.

Для удобства анализа обозначим все составные части силлогизма особыми знаками. С этой целью запишем силлогизм, расположив одну посылку под другой, а заключение, или вывод, — под второй посылкой. Отделим заключение от посылок горизонтальной чертой.

Пример силлогизма:

_{Все лягушки — амфибии.}

_{Все амфибии — позвоночные.}

——————————

^{Все лягушки — позвоночные.}

Рассмотрим сначала заключение, или вывод. В нём понятие предиката обозначим буквой Р, понятие субъекта — буквой S. Так как посылки выражают отношения принадлежности, то и вывод также выражает отношение принадлежности. Поэтому все отношения между понятиями, входящими в посылки и в вывод, будучи отношениями между содержанием понятий, будут в то же время и отношениями их объёмов. Очевидно, объём предиката в выводе больше объёма субъекта (объём понятия «позвоночные» больше объёма понятия «амфибии»).

На этом основании предикат вывода (Р) называется бо?льшим понятием, или бо?льшим термином силлогизма, а субъект вывода (S) — меньшим термином. Та посылка, в которую входит больший термин (Р), называется большей посылкой силлогизма. В нашем примере больший термин — понятие «позвоночные», меньший термин — понятие «лягушки», бо?льшая посылка — суждение «все амфибии —позвоночные». Та посылка, в которую входит меньший термин (S), называется меньшей посылкой силлогизма. В нашем примере меньшая посылка — суждение «все лягушки — амфибии».

Вывод «все лягушки — позвоночные» действительно обоснован данными посылками. Признав, что «все амфибии — позвоночные» и что «все лягушки — амфибии», мы не можем не признать, что «все лягушки — позвоночные».

Как же обоснован этот вывод? — В меньшей посылке мы установили отношение меньшего термина к некоторому третьему понятию — к понятию «амфибии». Меньшая посылка установила, что «все лягушки — амфибии», т. е. что весь объём понятия «лягушки» полностью входит в объём понятия «амфибии». В большей посылке мы установили отношение этого же самого третьего понятия к большему термину — к понятию «позвоночные». Бо?льшая посылка установила, что «все амфибии — позвоночные», т. е. что весь объём понятия «амфибии» полностью входит в объём понятия «позвоночные». В результате оказалось возможным установить — через третье понятие (понятие «амфибии») — связь между понятием «лягушки» и понятием «позвоночные»: так как все лягушки входят в число амфибий, а все амфибии, в свою очередь, входят в число позвоночных, то все лягушки должны также входить в число позвоночных. Или иначе: так как в число позвоночных входят все амфибии, а в число амфибий — все лягушки, то в число позвоночных должны входить все лягушки.

Третье понятие, посредством которого в выводе выясняется отношение между меньшим и бо?льшим терминами, называется средним термином силлогизма.

Как видно из примера, средний термин входит в каждую из посылок, но не входит в заключение, или в вывод, силлогизма. Нетрудно понять, почему это так. Цель силлогизма, как мы уже знаем, состоит в выяснении отношения между двумя понятиями S и Р. Средний термин появляется в силлогизме не потому, что средний термин нас интересует сам по себе. Он появляется потому, что только через отношение среднего термина к S и Р может, быть выяснено не видное непосредственно отношение между S и Р. Но выяснение отношения среднего термина к S и Р достигается уже в посылках силлогизма: бо?льшая посылка раскрывает отношение среднего термина к Р, меньшая — к S. Как только задача выяснения этих отношений выполнена, как только отношение между S и Р стало ясным из отношения каждого из них в отдельности к среднему термину, средний термин перестаёт быть предметом нашей мысли. Наша мысль направляется уже не на средний термин, а на то отношение между S и Р, которое было выяснено с помощью среднего термина. Поэтому в выводе, или в заключении, силлогизма выступают только S и Р.

Обозначим средний термин буквой М. Тогда наш силлогизм может быть представлен следующей схемой, или, как говорят в логике, «фигурой»:

Как ????видно из примера и из его схемы, порядок посылок никакой роли не играет: бо?льшая посылка может быть первой, а меньшая — второй и наоборот. От порядка посылок в силлогизме вывод, т. е. логическая связь между субъектом и предикатом, не зависит.

Обстоятельство это необходимо запомнить, чтобы не связывать названия «бо?льшая посылка» и «меньшая посылка» с тем порядком, в каком посылки следуют одна за другой. Независимо от этого порядка большей будет только та посылка, в которую входит больший термин, т. е. предикат вывода (Р), а меньшей — только та, в которую входит меньший термин, т. е. субъект вывода (S).

Силлогизмы могут иметь различное строение посылок, и потому самые выводы в них могут стоять в зависимости от различных правил. Логика устанавливает все эти правила и изучает все разновидности силлогизмов.

§ 10. Первая группа силлогизмов — так называемые простые категорические силлогизмы. Так называются силлогизмы, в которых вывод получается из двух посылок и в которых обе посылки суть суждения категорические.

Рассматривая встречающиеся в практике мышления простые категорические силлогизмы, можно заметить, что расположение понятий, или терминов, в посылках этих силлогизмов может быть различным.

Рассмотрим следующий силлогизм:

В нём средний термин в большей посылке является субъектом, а в меньшей — предикатом.

Силлогизм, в котором понятия, или термины, расположены таким образом, называется силлогизмом первой фигуры.

В нашем примере силлогизма первой фигуры меньшая посылка («все лягушки — амфибии») выясняет, что весь объём класса S входит как часть в более обширный объём класса М (см. рис. 38).

Рис. 38

Бо?льшая посылка («все амфибии — позвоночные») выясняет, что этот более обширный объём класса М весь входит как часть в ещё более обширный объём класса Р (см. рис. 39).

Рис. 39

Сопоставляя эти отношения понятий, выяснившиеся из посылок, устанавливаем в выводе («все лягушки — позвоночные») принадлежность класса S, имеющего наименьший объём, к классу Р, имеющему наибольший объём (см. рис. 40).

Рис. 40

§ 11. Рассмотрим теперь другой пример силлогизма:

_{Все звёзды светят собственным светом.}

_{Ни одна планета не светит собственным светом.}

—————————————————

^{Ни одна планета, не есть звезда.}

Вывод этот — силлогизм. В нём заключение, или вывод («ни одна планета не есть звезда»), получено из двух посылок. В посылках этих устанавливается отношение субъекта вывода («планета») и предиката вывода («звезда») к третьему, или среднему, понятию («тело, светящее собственным светом»). Именно через отношение среднего понятия к понятиям «планета» и «звезда» выясняется отношение этих последних между собой.

И действительно: бо?льшая посылка («все звёзды светят собственным светом») устанавливает, что весь объём класса Р входит в объём класса М (см. рис. 41).

Рис. 41

Меньшая посылка («ни одна планета не светит собственным светом»)устанавливает, что класс не принадлежит к классу М, т. е. что весь объём класса S целиком находится вне объёма класса М (см. рис. 42).

Рис. 42

Сопоставляя эти отношения понятий, выяснившиеся из посылок, заключаем в выводе («ни одна планета не есть звезда»), что класс S не принадлежит к классу Р, т. е. что весь объём класса S находится вне всего объёма класса Р (см. рис. 43).

Рис. 43

Присматриваясь к расположению терминов в посылках и в выводе этого силлогизма, замечаем, что это расположение

Р — М

S — M

———

S — Р

отличается от расположения терминов в силлогизме первой фигуры:

М — Р

S — M

———

S — Р

А именно: во втором силлогизме средний термин в обеих посылках — большей и меньшей — является предикатом. Силлогизм с таким расположением терминов называется силлогизмом второй фигуры.

§ 12. Рассмотрим третий пример силлогизма:

_{Все утконосы — животные, кладущие яйца.}

_{Все утконосы — млекопитающие.}

————————————————————

^{Некоторые млекопитающие — животные, кладущие яйца.}

И этот вывод —силлогизм. И в нём на основе устанавливаемого в двух посылках отношения понятия «млекопитающие» и понятия «животные, кладущие яйца» к третьему понятию («утконосы») устанавливается отношение субъекта к предикату в заключении.

Бо?льшая посылка («все утконосы — животные, кладущие яйца») устанавливает, что класс М принадлежит к классу Р, т.е. что весь объём класса М входит как часть в объём класса Р (см. рис. 44).

Рис. 44

Меньшая посылка («все утконосы — млекопитающие») устанавливает, что класс М принадлежит к классу S, т. е., что весь объём класса М входит как часть в объём класса S (см. рис. 45).

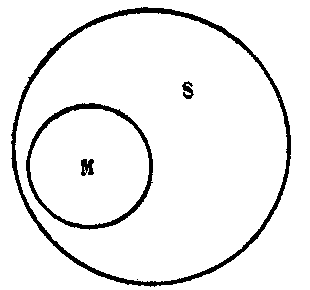
Рис. 45

Сопоставляя эти отношения понятий, выяснившиеся из посылок, заключаем в выводе («некоторые млекопитающие — животные, кладущие яйца»), что какая-то часть класса S принадлежит к классу Р, т. е. объём S в какой-то своей части совпадает с объёмом Р (см. рис. 46).

Рис. 46

И действительно, так как весь объём М целиком помещается как внутри объёма S, так и внутри объёма Р, то все те части объёма S, которые заняты объёмом М, будут в то же время и частями объёма Р. И наоборот: все те части объёма Р, которые заняты объёмом М, будут в то же время и частями объёма S.

Рассмотрим расположение терминов в последнем силлогизме:

М — Р

М — S (III)

———

S — P

Здесь расположение терминов отличается от их расположения в силлогизмах первой и второй фигуры:

А именно: в третьем силлогизме средний термин в обеих посылках оказывается субъектом. Силлогизм с таким расположением терминов называется силлогизмом третьей фигуры.

Различия между тремя фигурами простого категорического силлогизма представляют интерес не только потому, что термины в посылках этих силлогизмов размещены различным образом. Различное расположение терминов в посылках связано с различным отношением между содержанием и объёмом понятий, входящих в посылки и в выводы. И действительно: от того, будет ли, например, средний термин субъектом посылки или её предикатом, зависит распределённость среднего термина в посылках, т. е. возможность мыслить средний термин во всём объёме или только в части его объёма. То же справедливо и относительно большего и меньшего термина. В свою очередь от отношения между содержанием и объёмом понятий, входящих в посылки и в выводы, зависит различная ценность фигур силлогизма для логического мышления и знания, а потому различная роль, какую каждая из фигур играет в доказательствах и рассуждениях.

§ 13. Чтобы выяснить роль каждой фигуры, т. е. характер выводов, которые могут быть получены посредством этой фигуры, необходимо познакомиться с разновидностями фигур, или модусами.

Сравнивая различные выводы, сделанные по одной и той же фигуре, замечаем, что силлогизмы одной и той же фигуры могут различаться между собой качеством и количеством посылок и вывода.

Сравним два силлогизма:

Оба эти силлогизма — силлогизмы первой фигуры, так как в обоих средний термин является субъектом в большей и предикатом в меньшей посылке. Но в то же время между этими двумя силлогизмами первой фигуры имеется и различие. Состоит оно в различном качестве посылок и вывода. В первом силлогизме обе посылки и вывод — суждения общеутвердительные. Схема этого силлогизма:

А

А

—

А

Во втором силлогизме бо?льшая посылка есть суждение общеотрицательное, меньшая — общеутвердительное, вывод — суждение общеотрицательное. Схема этого силлогизма:

Е

А

—

Е

Сравним ещё два силлогизма:

Оба эти силлогизма — также силлогизмы первой фигуры, так как в обоих средний термин является субъектом в большей и предикатом в меньшей посылке. Но в то же время между этими двумя силлогизмами первой фигуры имеется и различие. Состоит оно в различном качестве и количестве посылок и вывода. В первом силлогизме и посылки и вывод по качеству — суждения утвердительные. По количеству же большая посылка — суждение общее, меньшая — частное, вывод — также частное. Схема этого силлогизма:

А

I

—

I

Во втором силлогизме бо?льшая посылка есть суждение общеотрицательное, меньшая — частноутвердительное, вывод — суждение частноотрицательное. Схема этого силлогизма:

Е

I

—

О

Сравнивая качество и количество выводов во всех четырёх примерах силлогизма первой фигуры, приведённых выше, видим, что в первом примере вывод — общеутвердительный («все бамбуковые — однодольные растения»), во втором — общеотрицательный («ни одно бамбуковое не есть двудольное растение»), в третьем - частноутвердительный («некоторые бесцветковые — споровые растения»), в четвёртом — частноотрицательный («некоторые светила — не звёзды»).

Разновидности силлогизмов одной и той же фигуры, обусловленные различным качеством и количеством посылок и выводов, называются модусами (от латинского слова, «modus», означающего «способ», «вид»).

§ 14. Итак, среди выводов простого категорического силлогизма могут встретиться выводы всех возможных видов качества и количества: А, Е, I и О. Но мы уже знаем, что различные по качеству и по количеству суждения имеют различное применение в знании и различную ценность для знания. Поэтому при изучении силлогизмов всех трёх фигур большой интерес представляет вопрос, какие именно модусы может дать каждая фигура силлогизма, иначе говоря, какими могут быть выводы этой фигуры по качеству и по количеству.

Для ответа на этот вопрос необходимо прежде всего исследовать, все ли теоретически возможные модусы, т. е. все ли сочетания посылок, отличающиеся только качеством и количеством, способны давать правильные выводы.

Исследование показывает, что не всякий теоретически возможный модус, т. е. не всякое сочетание качества и количества в посылках силлогизма, даёт правильный вывод.

Рассмотрим, например, суждения:

_{Все студенты обязаны держать экзамены.}

^{Все аспиранты — не студенты.}

В этих суждениях налицо три понятия, расположенные по схеме первой фигуры простого категорического силлогизма. Термин «студенты» в одной из посылок является субъектом, в другой — предикатом. В одной посылке устанавливается отношение терминй «студенты» к одному понятию, в другой — отношение того же термина к другому понятию.

Итак, расположение терминов в суждениях как будто в точности соответствует схеме первой фигуры:

М — Р

S — M

Первое суждение будет общеутвердительное, второе — общеотрицательное.

Схематически количество и качество этих суждений будет следующее:

А

Е

Но хотя расположение терминов в этом случае как будто отвечает условиям первой фигуры, правильный вывод из этих двух посылок невозможен. Из того, что «все студенты обязаны держать экзамены», и из того, что «все аспиранты — не студенты», никак нельзя вывести в качестве необходимого заключения, что, например, «аспиранты не обязаны держать экзамены». Хотя первая посылка выясняет отношение «студентов» к «лицам, обязанным держать экзамены»; а вторая — отношение «студентов» к «аспирантам», — отношения эти не таковы, чтобы из них видно было, каким должно быть отношение «аспирантов» к «лицам, обязанным держать экзамены». Как видно из рисунка (см. рис. 47), здесь логически возможны — при данных посылках — три случая.

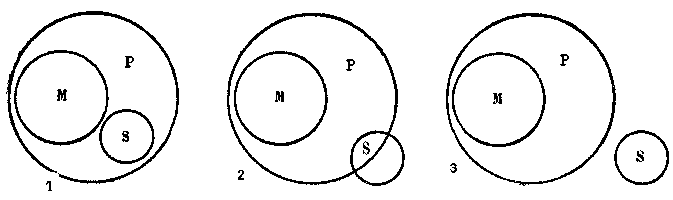
Рис. 47

Не будучи студентами (М), аспиранты (S) 1) могут все принадлежать к числу лиц, обязанных держать экзамены (Р), 2) могут принадлежать к числу этих лиц лишь в некоторой своей части и 3) могут вовсе не принадлежать к числу этих лиц.

Итак, некоторые модусы, например модус АЕ первой фигуры силлогизма, невозможны. Это значит, что качество и количество посылок в этих модусах не дают основания для правильного логического вывода. Поэтому для ответа на вопрос, какие модусы даёт каждая из трёх фигур простого категорического силлогизма, необходимо прежде всего выяснить условия или правила, которым должны удовлетворять посылки и входящие в эти посылки термины, чтобы вывод оказался действительно возможным. При этом оказывается, что существуют правила, общие для всех фигур силлогизма. Во всяком простом категорическом силлогизме, какова бы ни была его фигура, каков бы ни был модус этой фигуры, должны выполняться все общие для всех силлогизмов правила. Нарушение хотя бы одного из них делает умозаключение ошибочным.

Кроме правил, общих для всех фигур силлогизма, существуют и такие правила, которые являются особыми правилами для каждой фигуры силлогизма в отдельности. Правила эти обязательны для всех модусов данной фигуры силлогизма и не обязательны для модусов других фигур.

§ 15. Существуют десять правил, общих для всех фигур простого категорического силлогизма. Из этих десяти общих правил два определяют число терминов и число суждений, входящих в состав силлогизма. Два других правила определяют необходимые условия распределённости терминов в посылках и в выводах силлогизма. Остальные общие правила определяют необходимую связь между качеством и количеством посылок и качеством и количеством выводов (заключений) силлогизма.