Полная индукция

§ 11. Первый вид индукции образует полная индукция. Так называется индуктивное умозаключение, в котором общий вывод извлекается из ряда единичных посылок, исчерпывающих в своей сумме все возможные случаи или все возможные виды известного рода.

Пример полной индукции:

В этом умозаключении вывод есть общее суждение о целом роде (о всех конических сечениях). Общий вывод обосновывается рядом посылок, каждая из которых высказывает один и тот же предикат. Этот предикат высказывается не о целом роде, но лишь об одном из его видов: о круге, об эллипсе, о параболе, о гиперболе, — о каждом в отдельности. Особая посылка удостоверяет, что кроме перечисленных видов не существует никаких других видов конических сечений. Так как, предикат, утверждаемый каждой посылкой, оказался принадлежащим каждому из видов без исключения, то отсюда получается общий вывод, что этот предикат принадлежит всему роду.

Другой пример полной индукции был уже приведён выше — при разъяснении особенностей индуктивных умозаключений. В этом примере общий вывод — «все дни на прошлой неделе погода стояла пасмурная» — получился из посылок, выяснивших, что в неделе семь дней и что каждый из дней прошлой недели, в отдельности взятый, был пасмурный. Здесь, как и в предыдущем примере, общий вывод основывается на полном перечислении всех единичных случаев, сумма которых исчерпывает известный класс и которые характеризуются тем, что о каждом из них в отдельности высказывается один и тот же предикат. Единственное отличие этого вывода от предыдущего состоит в том, что здесь общий вывод получается из единичных посылок, в то время как в примере с коническими сечениями общий вывод есть вывод о роде, посылки же говорят только о видах этого рода. Но и в том и в другом случае — будут ли посылки, высказывающие предикат, суждениями единичными или суждениями о видах — в сравнении с заключением они всегда будут иметь частный характер.

Самый ход умозаключения в общих случаях один и тот же. Состоит он в том, что предикат, высказываемый посылками о каждом отдельном экземпляре класса или о каждом отдельном виде, в заключении высказывается, о всём классе или о всём роде, т. е. переносится на весь класс или род.

§ 12. На чём основывается логическое право такого переноса? Оно основывается на полном тождестве объёмов понятий класса (или рода), о котором говорит общий вывод, и суммы объёмов понятий всех экземпляров (или всех видов рода), о которых говорят частные посылки. В свою очередь это тождество объёмов понятий основывается на том, что и весь класс (или род), о которых говорится в выводе, и каждый экземпляр класса (или каждый вид рода), о которых говорится в частных посылках, тождественны по содержанию. Это значит, что признаки, по которым мыслится класс (или род), и признаки, по которым мыслится каждый экземпляр класса (или каждый вид рода), — одни и те же. Это — те именно признаки, которые мыслятся в предикате частных посылок.

Иными словами, признаки, мыслимые в частных предметах известного класса или в частных видах известного рода, мы переносим — в случае выводов полной индукции — на весь класс или на весь род.

Но право на такой перенос мы имеем только в том случае, когда мы рассмотрели действительно все предметы, входящие в класс (или все виды, входящие в род). Только в этом случае между предметом общего суждения о всём классе (или роде) и суммой предметов частных суждений об отдельных экземплярах класса (или видах рода), с которых переносится предикат, будет существовать полное логическое тождество, дающее право на общий вывод.

Напротив, в случаях, когда частные посылки не исчерпывают всех экземпляров класса (или всех видов рода), для переноса предиката, мыслимого о частных предметах класса (или рода), на весь класс (или род) нет достаточного основания. В таких случаях общий вывод легко может оказаться ошибочным.

Примером такого ошибочного вывода полной индукции может быть заключение древних астрономов о прямых движениях внешних планет. Астрономы эти ничего не знали о существовании внешних планет Урана, Нептуна, Плутона, а также о существовании спутников планет. Не подозревая об их существовании и зная из наблюдений над известными им тремя внешними планетами, что каждая из них по общему правилу движется относительно звёзд с запада на восток, т. е. так называемым прямым движением, астрономы эти сделали вывод, будто все внешние планеты движутся прямым движением.

Вывод этот оказался ошибочным. Его ошибочность заключалась в том, что не были приняты во внимание все входящие в класс внешних планет экземпляры этого класса. Иными словами, ошибочной оказалась посылка, утверждавшая, будто кроме Марса, Юпитера и Сатурна нет больше никаких внешних планет. В действительности оказалось, что класс внешних планет не исчерпан тремя планетами, известными древним. Более того: оказалось, что некоторые из спутников внешних планет имеют не прямые, а обратные движения. Как только был установлен этот факт, рухнуло основание для общего вывода о прямых движениях всех внешних планет.

Ошибка, состоящая в том, что неполный обзор экземпляров класса или видов рода принимается за исчерпывающий и потому рассматривается как основание для общего вывода о всём классе или обо всём роде, встречается часто. В таких случаях полная индукция оказывается мнимой полной индукцией, а её общее заключение часто оказывается ошибочным. Уверенность, что род исчерпывается всеми известными в настоящее время его видами или класс — всеми известными доселе экземплярами, часто не имеет достаточного основания.

§ 13. Указанными чертами полной индукции определяется и область её применения и её значение для знания. Полная индукция не даёт знания о других предметах, кроме тех, которые поочерёдно перечислены в частных посылках. Так, общий вывод о конических сечениях в нашем первом примере полной индукции не распространяется ни на какие новые предметы сравнительно с теми, о которых шла речь в частных посылках. Тот предикат, который каждая отдельная посылка повторно высказывала о круге, об эллипсе, о параболе и о гиперболе, не переносится в заключении ни на какие иные или новые кривые, кроме перечисленных. В этом смысле, т. е. по отношению к количеству предметов, на какие переносится общий вывод, полная индукция не даёт нового знания сравнительно с тем знанием, каким мы располагали в посылках.

Однако, не распространяясь на новые предметы, общий вывод полной индукции характеризует те же самые, предметы с некоторой новой стороны. Субъектом суждения в каждой частной посылке был каждый отдельный предмет класса (или отдельный вид рода) в качестве именно отдельного и только отдельного предмета или вида. Напротив, в общем заключении субъектом суждения оказываются те же предметы, но уже рассматриваемые в качестве не отдельных, а в качестве некоторого класса или некоторого рода, т. е. в качестве некоторой логической группы. Поэтому умозаключение полной индукции не есть пустое повторение в форме общего вывода того, что уже сполна мыслилось в частных посылках.

Научная ценность выводов полной индукции зависит от того, будут ли частные посылки, обосновывающие вывод, суждениями об отдельных предметах класса или о видах рода. Если частные посылки представляют суждения об отдельных предметах класса, то общий вывод, согласно сущности полной индукции, возможен лишь при условии, когда перечислены и рассмотрены все экземпляры, из которых состоит класс. В таких выводах число экземпляров класса, очевидно, должно быть ограниченным, так как обзор экземпляров должен быть исчерпывающим. Поэтому выводы в этом случае представляют меньшую ценность для знания.

Но если частные посылки, обосновывающие вывод, представляют суждения о видах, то ограниченность числа видов, из которых состоит род, не препятствует тому, чтобы общая сумма экземпляров, составляющих род, была неисчислимо большой. Хотя имеется всего четыре вида конических сечений, но так как каждый из них обнимает бесчисленное множество экземпляров, то и вся группа конических сечений, на которую в выводе переходит предикат частных посылок, будет группой, состоящей из бесчисленного множества экземпляров. Такие выводы, в которых известное общее свойство группы может быть отнесено к каждому из неисчислимо большого количества членов этой группы, представляют бо?льшую ценность для знания, чем выводы о группе, состоящей из ограниченного числа экземпляров.

Умозаключение от принадлежности предиката каждому из видов рода в отдельности к принадлежности этого же предиката целому роду часто применяется в доказательствах математических наук. При помощи полной индукции геометрия доказывает теорему, согласно которой всякий угол, вписанный в круг, измеряется половиной центрального угла, опирающегося на ту же дугу. Геометрия доказывает, что положение это справедливо, во-первых, для случая, когда центр круга лежит между сторонами вписанного в круг угла, во-вторых, для случая, когда центр круга лежит на одной из сторон вписанного в круг угла, и, в-третьих, когда центр круга лежит вне обеих сторон вписанного в круг угла (см. рис. 65).

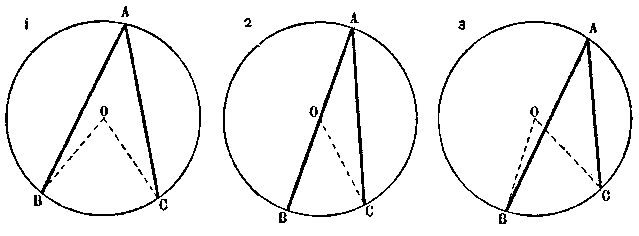
Рис. 65

Так как этими тремя случаями исчерпываются все возможные виды понятия вписанного в круг угла и так как доказанное положение оказывается справедливым относительно каждого из видов рода в отдельности, то отсюда геометрия заключает по методу полной индукции, что положение это будет справедливо и относительно всего рода, т. е. относительно всякого вписанного в круг угла.

§ 14. В предварительном разъяснении понятия об индукции были указаны черты, отличающие индуктивные умозаключения от силлогизмов. Там же было сказано, что наряду с чертами, отличающими индуктивные выводы от силлогизмов, имеются и общие черты между ними.

Сказанное справедливо и относительно полной индукции. Умозаключении полной индукции, отличаясь от силлогизмов, как все индуктивные выводы, способностью давать общие выводы из частных посылок, в то же время сходны с силлогизмами в трёх отношениях.

Во-первых, умозаключения полной индукции, так же как и силлогизмы, дают в отличие от других видов индукции не только вероятные, но вполне достоверные выводы. Правда, условием достоверности этих выводов является исчерпывающий обзор всех экземпляров, составляющих класс, или всех видов, составляющих род, на который в заключении переносится предикат частных посылок. Но ведь и в силлогизмах условием достоверности вывода всегда является достоверность посылок, обосновывающих вывод. Только возможность в отдельных случаях ошибочно признать недостоверную посылку за достоверную приводит к ошибочному выводу, но от этого нисколько не колеблется общее свойство силлогизмов — давать при условии достоверности посылок вполне достоверные выводы.

Точно так же ошибочное признание неполного обзора экземпляров класса или видов рода за полный их обзор приводит к ошибочному обобщению, но нисколько не противоречит тому, что при условии действительно исчерпывающего перечня всех экземпляров класса или всех видов рода заключение полной индукции, приписывающее предикат всему классу или роду, будет вполне достоверным.

§ 15. Вторая черта, сближающая полную индукцию с силлогистическими умозаключениями, состоит в том, что посылки и выводы полной индукции, в отличие от посылок и выводов других видов индукции, обычно являются суждениями о принадлежности. Так, в примере с общим выводом о конических сечениях и каждая посылка и вывод утверждают принадлежность известного свойства — способности пересекаться прямой не более чем в двух точках — не только каждому отдельному виду конических сечений, но и всему их роду. Напротив, в других видах индукции, о которых речь впереди, в заключении индуктивного вывода обычно устанавливается причинное отношение.

§ 16. В-третьих, кроме общего сходства полной индукции со всеми силлогизмами существует ещё особое сходство между выводами полной индукции и простыми категорическими силлогизмами третьей фигуры.

Общим между ними является самый ход умозаключения и основание, на которое оно опирается. И действительно, в силлогизмах третьей фигуры, так же как и в выводах полной индукции, мы имеем в заключении переход предиката с логического вида на логический род.

Например:

Все сумчатые — двуутробные.

Все сумчатые — млекопитающие.

————————————

След., некоторые млекопитающие — двуутробные.

Силлогизм этот — третьей фигуры. В нём предикат «двуутробные» переносится в заключении с «сумчатых» на «млекопитающих». Но «сумчатые», как видно из меньшей посылки, составляют по отношению к «млекопитающим» только один из видов всего рода «млекопитающих». Именно поэтому, приписывая предикат «двуутробные» роду «млекопитающих», заключение приписывает этот предикат не всему роду «млекопитающих», но лишь той части объёма этого рода, с которой совпадает объём его вида «сумчатые».

Отсюда видно, что частный характер заключений, получающихся по третьей фигуре силлогизма, ничуть не препятствует тому, что самый ход вывода по третьей фигуре состоит в переносе предиката с вида на род. Из того, что заключения третьей фигуры — всегда только частные, никак не следует, что самый ход вывода по третьей фигуре состоит в движении от рода к виду. Из этого следует только то, что, выполняя перенос предиката с вида на род, заключение переносит предикат большей посылки с вида не на весь род, но лишь на некоторую его часть.

Но тот же самый ход умозаключения имеет место и при полной индукции. И здесь заключение переносит предикат, приписывавшийся в каждой из частных посылок только одному из видов рода, на весь род. То, что в каждой частной посылке утверждалось об одном каком-нибудь виде конических сечений — отдельно о круге, об эллипсе, о параболе, о гиперболе, — в заключении утверждается о всём роде конических сечений.

Различие между полной индукцией и третьей фигурой силлогизма состоит не в ходе умозаключения, а в результате этого хода. Результатом его в случае третьей фигуры будет всегда только частное, в случае же полной индукции — всегда общее суждение.

Причина этого различия — в неодинаковой полноте обзора тех видов, предикат которых переносится на род. В случае полной индукции обзор видов, выполненный в частных посылках — исчерпывающий, т. е. охватывает весь род. Поэтому и предикат, переходящий в заключении с видов на род, переходит не на часть рода, а на весь род.

Напротив, в случае третьей фигуры предикат, высказываемый большей посылкой, утверждается только об одном виде рода. Поэтому предикат этот, переходя в заключении с вида на род, переходит не на весь род, а лишь на ту его часть, объём которой совпадает с объёмом вида.

Но и в том и в другом случае — переходит ли предикат на весь род или только на какую-то его часть — предикат переходит с видов на род. Общим основанием для возможности этого перехода является тождество между объёмом видов и объёмом рода. В случае полной индукции это тождество будет полное, так как учтены все виды рода, в случае третьей фигуры — всего лишь частичное, так как учтён только один вид.