2.2. Вычисления

2.2. Вычисления

В этом разделе мы поговорим о вычислениях. Под вычислением (или алгоритмом) я подразумеваю действие некоторой машины Тьюринга, или, иными словами, действие компьютера, задаваемое той или иной компьютерной программой. Не следует забывать и о том, что понятие вычисления включает в себя не только выполнение обычных арифметических действий — таких, например, как сложение или умножение чисел, — но и некоторые другие процессы. Так, частью вычислительной процедуры могут стать и вполне определенные логические операции. В качестве примера вычисления можно рассмотреть следующую задачу:

(А) Найти число, не являющееся суммой квадратов трех чисел.

Под «числом» в данном случае я подразумеваю «натуральное число», т.е. число из ряда

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ….

Под квадратом числа понимается результат умножения натурального числа на само себя, т.е. число из ряда

0, 1, 4, 9, 16, 25, 36, …;

представленные в этом ряду числа получены следующим образом:

0 ? 0 = 0², 1 ? 1 = 1², 2 ? 2 = 2², 3 ? 3 = 3², 4 ? 4 = 4², 5 ? 5 = 5², 6 ? 6 = 6², ….

Такие числа называются «квадратами», поскольку их можно представить в виде квадратных матриц (пустой матрицей в начале строки обозначен 0):

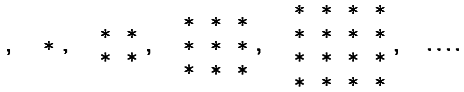
С учетом вышесказанного решение задачи (А) может происходить следующим образом. Мы поочередно проверяем каждое натуральное число, начиная с 0, на предмет того, не является ли оно суммой трех квадратов. При этом, разумеется, рассматриваются только те квадраты, величина которых не превышает самого числа. Таким образом, для каждого натурального числа необходимо проверить некоторое конечное количество квадратов. Отыскав тройку квадратов, составляющих в сумме данное число, переходим к следующему натуральному числу и снова ищем среди квадратов (не превышающих по величине рассматриваемое число) такие три, которые дают в сумме это самое число. Вычисление завершается лишь тогда, когда мы находим натуральное число, которое невозможно получить путем сложения любых трех квадратов. Попробуем применить описанную процедуру на практике и начнем наше вычисление с нуля. Нуль равен 0² + 0² + 0², что, безусловно, является суммой трех квадратов. Далее рассматриваем единицу и находим, что она не равна 0² + 0² + 0², однако равна 0² + 0² + 1². Переходим к числу 2 и выясняем, что оно не равно ни 0² + 0² + 0², ни 0² + 0² + 1², но равно 0² + 1² + 1². Затем следует число 3 и сумма 3 = 1² + 1² + 1²; далее — число 4 и сумма 4 = 0² + 0² + 2²; после 5 = 0² + 1² + 2² и 6 = 1² + 1² + 2² переходим к 7, и тут обнаруживается, что ни одна из троек квадратов (всех возможных троек квадратов, каждый из которых не превышает 7)

0² + 0² + 0²   0² + 0² + 1²   0² + 0² + 2²   0² + 1² + 1²   0² + 1² + 2²

0² + 2² + 2²   1² + 1² + 1²   1² + 1² + 2²   1² + 2² + 1²   2² + 2² + 2²

не дает в сумме 7. На этом этапе вычисление завершается, а мы делаем вывод: 7 есть одно из искомых чисел, так как оно не является суммой квадратов трех чисел.